АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнения в полных дифференциалах

Читайте также:
  1. VI Дифференциальные уравнения
  2. Алгебраические уравнения
  3. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  4. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  5. Геометрическая оптика.отражение и преломление света. законы отражения и преломления.Зеркала и линзы.Уравнения для зеркал и линз.оптические приборы.
  6. Геометрический образ уравнения состояния.
  7. Дети из неполных семей
  8. Дифференциальные уравнения 1 порядка с разделяющимися переменными
  9. Дифференциальные уравнения движения вязкой жидкости. Граничные условия.
  10. Дифференциальные уравнения и передаточные функции замкнутых систем управления
  11. Дифференциальные уравнения первого порядка с разделяющимися переменными.
  12. Дифференциальные уравнения первого порядка.

Определение. Д.у. 1-го порядка вида:

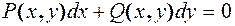
называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции . Т.к. правая часть уравнения =0, то . Проверка типа уравнения:

.

Как находим функцию u=u(x,y)?

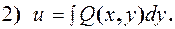
Сравним полученные функции и составим функцию u=u(x,y).

Пример. Решить уравнение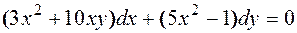

Проверим условие равенства частных производных:

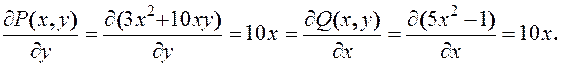
Þ Д.у. является уравнением в полных дифференциалах.

Определим функцию u.

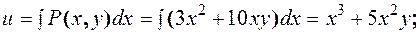
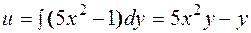
Þ решение д.у.: .


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)