 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Узагальнення задачі
Математичні моделі розміщення підприємств
Одним з найважливіших питань, що відносить як до міжгалузевого, такі до територіального планування, є питання розміщення підприємств. Де побудувати підприємство? Якщо близько до сировини, то далеко від споживача. Якщо близько до споживача, то далеко від сировини. Також треба врахувати забезпечення трудовими ресурсами і багато інших факторів.
Лінійна статична модель розміщення виробництва одного продукту. Нехай у деяких пунктах  розміщені підприємства, що виробляють деякий продукт. У пунктах
розміщені підприємства, що виробляють деякий продукт. У пунктах  знаходяться пункти споживання цього продукту. Відомі величини:
знаходяться пункти споживання цього продукту. Відомі величини:
 – максимально можливий об’єм виробництва у пункті
– максимально можливий об’єм виробництва у пункті  ,
, 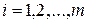 ,
,
 – потреби споживачів у пункті
– потреби споживачів у пункті  ,
,  ,
,
 – витрати на виробництво одиниці продукції у пункті
– витрати на виробництво одиниці продукції у пункті  ,
, 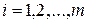 ,
,
 – витрати на транспортування одиниці продукції з пункту
– витрати на транспортування одиниці продукції з пункту  у пункт споживання
у пункт споживання  ,
, 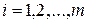 ,
,  ,
,
Необхідно визначати такий план виробництва продукції у кожному з пунктів виробництва та такий план перевезення продукції від виробників до постачальників, при якому сумарні витрати будуть найменшими.
Позначимо
 – об’єм виробництва продукції у пункті
– об’єм виробництва продукції у пункті  ,
, 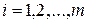 ,
,
 – об’єм продукції, що буде перевозитися з пункту
– об’єм продукції, що буде перевозитися з пункту  у пункт споживання
у пункт споживання  ,
, 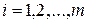 ,
,  ,
,
Математична модель задачі
| Обмеження | Інтерпретація |
 , , 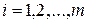 , ,  , ,
| об’єми перевезень не можуть бути від’ємними |
 , , 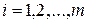 , ,
| об’єм вивезеної продукції від виробника  має дорівнювати об’єму виробленої ним продукції має дорівнювати об’єму виробленої ним продукції
|
 , , 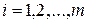 , ,
| об’єм вивезеної продукції від виробника  не повинен перевищувати максимально можливих об’ємів виробництва не повинен перевищувати максимально можливих об’ємів виробництва
|
 , ,  , ,
| потреби споживачів потрібно задовольнити |
Цільова функція (виражає зальні витрати на виробництво і перевезення)
 .
.
Тут
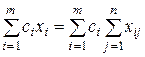 – загальні витрати на виробництво продукції,
– загальні витрати на виробництво продукції,
 – загальні витрати на перевезення продукції.
– загальні витрати на перевезення продукції.
Дана модель є звичайною транспортною задачею.
Узагальнення задачі
Врахування масштабів виробництва. Очевидно модель є дуже спрощеною, так, наприклад, вартість виробництва одиниці продукції залежить від об’ємів виробництва (чим більші об’єми – тим вартість виробництва одиниці продукції є меншою). В цьому випадку вартість виробництва одиниці продукції у пункті  виражається у вигляді відповідної функції
виражається у вигляді відповідної функції
 ,
,
і цільова функція
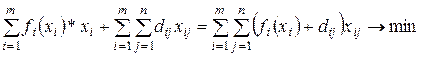
буде нелінійною.
Врахування обмеженості ресурсів. Ресурси можуть бути обмеженими. Обмеження можуть мати вигляд
 ,
,
де
 – кількість видів ресурсів,
– кількість видів ресурсів,
 – норма споживання
– норма споживання  -го ресурсу на виробництва одиниці продукції у пункті виробництва
-го ресурсу на виробництва одиниці продукції у пункті виробництва  ,
,
 – наявна кількість ресурсів
– наявна кількість ресурсів  го виду.
го виду.
Обмеженість пропускних здатностей мереж. Обмеження можуть мати вигляд
 ,
,
де  – максимальна пропускна здатність ділянки мережі, що з’єднує
– максимальна пропускна здатність ділянки мережі, що з’єднує  -тий та
-тий та 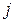 -тий пункти.
-тий пункти.
Варіантна математична модель розміщення підприємств. Необхідно визначити потужність підприємств з врахуванням дискретної зміни варіантів потужностей та план перевезень, що дозволить мінімізувати загальні витрати.
Введемо позначення
 – кількість підприємств, що виготовляють продукцію,
– кількість підприємств, що виготовляють продукцію,
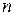 – кількість споживачів,
– кількість споживачів,
 – номер варіанту розвитку підприємства,
– номер варіанту розвитку підприємства,
 – кількість можливих варіантів розвитку
– кількість можливих варіантів розвитку  -го підприємства,
-го підприємства,
 – потужність
– потужність  -го підприємства згідно з
-го підприємства згідно з  -м варіантом,
-м варіантом,
 – об’єми споживання продукту
– об’єми споживання продукту 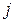 -им споживачем,
-им споживачем,
 – затрати на одиницю продукції згідно з
– затрати на одиницю продукції згідно з  -тим варіантом,
-тим варіантом,
 – вартість перевезення одиниці продукції з
– вартість перевезення одиниці продукції з  -го підприємства до
-го підприємства до 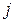 -го споживача,
-го споживача,
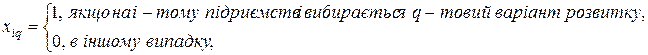
 – об’єм перевезень продукції з
– об’єм перевезень продукції з  -го підприємства до
-го підприємства до 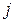 -го споживача,
-го споживача,
Математична модель задачі
| Обмеження | Інтерпретація |
 , ,
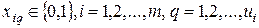 , ,
| |
 , ,
| на кожному з підприємств повинен бути вибраний тільки один з варіантів або ж підприємство треба закрити, якщо не вибрано жодного (сума дорівнює нулю) |
 , ,
| потреби споживачів повинні бути задоволені |

| у кожному з пунктів виробництва об’єм вивезеної продукції  не повинен перевищувати об’єму виробленої продукції не повинен перевищувати об’єму виробленої продукції 
|
Цільова функція
 ,
,
тут
 – витрати на виробництво продукції,
– витрати на виробництво продукції,
 – витрати на перевезення.
– витрати на перевезення.
Математична модель розміщення пунктів виробництва у мережевій постановці. На транспортній мережі відмічено пункти виробництва і пункти споживання. Мережа представлена у вигляді графа, що складається з вершин і дуг. Відомі потреби у продукції у кожній вершині графа і потужність діючих підприємств. Потрібно визначити потужності підприємств і транзитні потоки, які при заданих обмеженнях дозволять задовольнити потреби споживачів з мінімальними сумарними затратами.
Введемо позначення
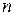 – кількість пунктів (вузлів) транспортної мережі,
– кількість пунктів (вузлів) транспортної мережі,
 – затрати на виробництво продукції у
– затрати на виробництво продукції у  -товому пункті мережі,
-товому пункті мережі,
 – максимальна виробнича потужність
– максимальна виробнича потужність  -го пункту,
-го пункту,
 –об’єм споживання продукції у
–об’єм споживання продукції у 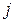 -тому пункті,
-тому пункті,
 –затрати на перевезення одиниці продукції з
–затрати на перевезення одиниці продукції з  -го пункту в
-го пункту в 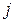 -товий,
-товий,
 – множина усіх дуг графа,
– множина усіх дуг графа,
 – множина вершин виробництва продукції,
– множина вершин виробництва продукції,
 – множина вершин споживання продукції,
– множина вершин споживання продукції,
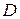 – множина проміжних транзитних пунктів, у яких продукція ні виробляється, ні споживається,
– множина проміжних транзитних пунктів, у яких продукція ні виробляється, ні споживається,
 – об’єми перевезень з
– об’єми перевезень з  -го пункту в
-го пункту в 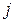 -товий
-товий
Математична модель задачі
| Обмеження | Інтерпретація |
 , , 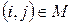
| Об’єми перевезень не можуть бути від’ємними |
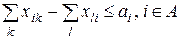
| Різниця між кількістю вивезеної продукції  і кількістю ввезеної і кількістю ввезеної 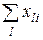 є кількістю виробленої продукції у цьому пункті і не може перевищувати його виробничих потужностей є кількістю виробленої продукції у цьому пункті і не може перевищувати його виробничих потужностей 
|

| Різниця між кількістю ввезеної продукції  і кількістю вивезеної і кількістю вивезеної  дорівнює кількості продукції, що залишається у цьому пункті і повинна дорівнювати потребам споживача цього пункту дорівнює кількості продукції, що залишається у цьому пункті і повинна дорівнювати потребам споживача цього пункту 
|

| Різниця між кількістю вивезеної продукції  і кількістю ввезеної і кількістю ввезеної 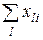 у транзитних пунктах повинна дорівнювати нулю у транзитних пунктах повинна дорівнювати нулю
|
Цільова функція

тут
 – витрати на виробництво продукції,
– витрати на виробництво продукції,
 – витрати на перевезення.
– витрати на перевезення.
Статична математична модель багатоетапного процесу розміщення пунктів виробництва. Розглядається випадок, коли виробництво здійснюється у декілька етапів – добування сировини, переробка на декількох підприємствах і потім споживання. Необхідно побудувати оптимальний план усіх етапів виробництва від добування сировини до кінцевого споживання.
Моделі розглядуваного процесу можуть бути варіантні або безваріанті.
Безваріанта модель багатоетапного процесу виробництва.
Введемо позначення
 – номер етапу;
– номер етапу;
 – кількість усіх етапів;
– кількість усіх етапів;
 – кількість підприємств, що здійснюють обробку сировини на етапі
– кількість підприємств, що здійснюють обробку сировини на етапі  ;
;
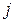 – номер споживача;
– номер споживача;
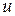 – номер підприємства на проміжковому етапі (включаючи перший етап);
– номер підприємства на проміжковому етапі (включаючи перший етап);
 – максимально можливий об’єм виробництва на
– максимально можливий об’єм виробництва на 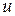 -тому підприємстві етапу
-тому підприємстві етапу  (
( );
);
 – об’єм споживання продукції у
– об’єм споживання продукції у 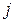 -тому пункті на останньому етапі (
-тому пункті на останньому етапі ( );
);
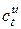 – затрати на переробку одиниці продукції на
– затрати на переробку одиниці продукції на 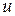 -тому підприємстві етапу
-тому підприємстві етапу  ;
;
 – затрати на перевезення одиниці продукції з
– затрати на перевезення одиниці продукції з 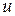 -того підприємства
-того підприємства  -го етапу в
-го етапу в  -те підприємство
-те підприємство  -го етапу;
-го етапу;
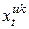 – об’єм перевезення продукції з
– об’єм перевезення продукції з 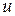 -го підприємства
-го підприємства  -го етапу, в
-го етапу, в  -те підприємство
-те підприємство  -го етапу.
-го етапу.
Кожне  -те підприємство споживачем сировини або напівфабрикатів, що виготовляються на підприємствах попереднього етапу. Це означає, що величини
-те підприємство споживачем сировини або напівфабрикатів, що виготовляються на підприємствах попереднього етапу. Це означає, що величини  представлені в однорідних одиницях виміру за допомогою перерахунку на одиничний уявний продукт.
представлені в однорідних одиницях виміру за допомогою перерахунку на одиничний уявний продукт.
Математична модель задачі складається з цільової функції
 ,
,
де
 – загальні витрати на виробництво продукції,
– загальні витрати на виробництво продукції,
 – загальні витрати на перевезення.
– загальні витрати на перевезення.
та обмежень
| Обмеження | Інтерпретація |
 , ,  , ,  , , 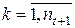
| Об’єми перевезень не можуть бути від’ємними |
 , ,  , , 
| об’єм вивезеної продукції з підприємств на кожному з етапів не повинен перевищувати їх максимальний об’єм виробництва |
 , ,  , , 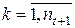
| об’єм ввезеної продукції з підприємств попереднього етапу для переробки не повинен перевищувати їх максимального об’єму виробництва |
 , ,  , , 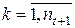
| на кожному підприємстві об’єм ввезеної продукції з попереднього етапу повинен дорівнювати об’єму вивезеної продукції з цього підприємства на підприємства наступного етапу |
 , ,  . .
| потреби споживачів повинні бути задоволені |
Динамічна модель розміщення виробництва. Розглядається випадок, коли розміщення пунктів виробництва розглядається протягом певного періоду часу, протягом якого об’єми виробництва підприємств можуть нарощуватися.
Введемо позначення
 – рік планового періоду;
– рік планового періоду;
 – кількість років планового періоду;
– кількість років планового періоду;
 – номер підприємства;
– номер підприємства;
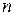 – кількість підприємств;
– кількість підприємств;
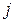 – номер споживача;
– номер споживача;
 – кількість споживачів;
– кількість споживачів;
 – максимальна потужність
– максимальна потужність  -го підприємства у
-го підприємства у  -му році;
-му році;
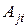 – потреба
– потреба 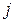 -го споживача у
-го споживача у  -му році;
-му році;
 – затрати на виробництво одиниці продукції у
– затрати на виробництво одиниці продукції у  -му році;
-му році;
 – вартість перевезення одиниці продукції з
– вартість перевезення одиниці продукції з  -го підприємства до
-го підприємства до 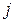 -го споживача у
-го споживача у  -му році;
-му році;
 – об’єм виробництва на
– об’єм виробництва на  -тому підприємстві у
-тому підприємстві у  -му році;
-му році;
 – об’єм перевезення з
– об’єм перевезення з  -го підприємства до
-го підприємства до 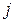 -го споживача у
-го споживача у  -му році.
-му році.
Математична модель задачі складається з цільової функції
 ,
, 
де
 – загальні витрати на виробництво продукції,
– загальні витрати на виробництво продукції,
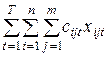 – загальні витрати на перевезення продукції,
– загальні витрати на перевезення продукції,
та обмежень
| Обмеження | Інтерпретація |
 , ,  , ,  , , 
| Об’єми перевезень не можуть бути від’ємними |
 , ,  , , 
| об’єм виробленої продукції, що дорівнює сумарному об’єму вивезеної продукції з цього підприємства, не повинен перевищувати максимального об’єму виробництва цього підприємства |
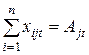 , ,  , ,  . .
| потреби споживачів повинні бути задоволені у кожному році планового періоду |
 , , 
| обмеження, що забезпечують неспадання обсягів виробництва підприємств |
Приклади задач розміщення виробництва.
Задача 1. Відомі максимально можливі об’єми випуску однотипної продукції на трьох заводах: 460, 340 та 300 тон відповідно. Потреби продукції чотирьох споживачів на цю продукцію складають: 350, 200 450 та 100 тон. Відомі також витрати на виробництво одиниці продукції на кожному заводі: 9,8 та 2 гривні, відповідно, перевезення однієї одиниці продукції від заводів до споживачів
| Споживач №1 | Споживач №2 | Споживач №3 | Споживач №4 | |
| Завод №1 | ||||
| Завод №2 | ||||
| Завод №3 |
Знайти оптимальний план прикріплення споживачів до заводів, при якому сумарні затрати на виробництво і транспортування будуть мінімальними.
Розв’язання
Позначимо
 – об’єм продукції, що буде перевозитися від
– об’єм продукції, що буде перевозитися від  -го заводу до
-го заводу до 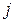 -го споживача
-го споживача  .
.
Транспортна задача є збалансованою (460+340+300=350+200+450+100).
Математична модель задачі складається з цільової функції
 де
де
 – загальні витрати на виробництво продукції,
– загальні витрати на виробництво продукції,
 – загальні витрати на перевезення
– загальні витрати на перевезення
та обмежень на випуск продукції
 ,
,
 ,
,
 ,
,
обмежень на споживання продукції
 ,
,
 ,
,
 ,
,
 ,
,
невід’ємності об’ємів перевезень
 .
.
Поиск по сайту: