 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Молекулярная физика. Вывод уравнения состояния идеального газа С помощью равенства (1) получим уравнение состояния идеального газа
| Вывод уравнения состояния идеального газа | С помощью равенства
 (1)
получим уравнение состояния идеального газа, связывающее между собой макроскопические параметры: давление, объем и температуру. Если известно полное число частиц газа (1)
получим уравнение состояния идеального газа, связывающее между собой макроскопические параметры: давление, объем и температуру. Если известно полное число частиц газа  , занимающего объем , занимающего объем  , то число частиц в единице объема , то число частиц в единице объема
 .
С учетом последнего выражение (1) приводится к виду .
С учетом последнего выражение (1) приводится к виду
 . (2)
Умножив и разделив правую часть равенства на молярную массу . (2)
Умножив и разделив правую часть равенства на молярную массу
 , (3)
имеем , (3)
имеем
 или (4) или (4)
 (5)
где (5)
где  – масса газа, – масса газа,  . .
 – молярная газовая постоянная (универсальная газовая постоянная). – молярная газовая постоянная (универсальная газовая постоянная).
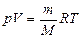 . (6)
Уравнение (6) есть уравнение состояния идеального газа, связывающее три макроскопических параметра (давление, объем и температуру) газа данной массы. По-другому оно называется уравнением Клапейрона-Менделеева.
Уравнение Клапейрона – Менделеева справедливо для идеального газа любого химического состава. Единственной величиной, определяющей специфику газа, является молярная масса. Состояние данной массы газа однозначно определяется заданием двух макроскопических параметров . (6)
Уравнение (6) есть уравнение состояния идеального газа, связывающее три макроскопических параметра (давление, объем и температуру) газа данной массы. По-другому оно называется уравнением Клапейрона-Менделеева.
Уравнение Клапейрона – Менделеева справедливо для идеального газа любого химического состава. Единственной величиной, определяющей специфику газа, является молярная масса. Состояние данной массы газа однозначно определяется заданием двух макроскопических параметров  , ,  или или  . Третий параметр . Третий параметр  соответственно определяется из уравнения Клапейрона – Менделеева.
С помощью уравнения состояния можно описывать процессы сжатия и расширения, нагревания и охлаждения идеального газа. соответственно определяется из уравнения Клапейрона – Менделеева.
С помощью уравнения состояния можно описывать процессы сжатия и расширения, нагревания и охлаждения идеального газа.
| ||||
| Определение изопроцесса | Процессы, протекающие в газе при постоянной массе и неизменном значении одного из параметров (p, V или T) называют изопроцессами.
Уравнения, описывающие эти процессы, могут быть получены из уравнения Клапейрона-Менделеева
 , (1)
хотя исторически они были получены экспериментально. , (1)
хотя исторически они были получены экспериментально.
| ||||
| Изотермический процесс | Процесс изменения состояния газа при постоянной массе ( ) и температуре ( ) и температуре ( ) называют изотермическим. Согласно уравнению состояния идеального газа (1) изотермический процесс имеет вид: ) называют изотермическим. Согласно уравнению состояния идеального газа (1) изотермический процесс имеет вид:
 (2)
Для газа постоянной массы и температуры произведение давления газа на его объем постоянно.
Этот закон экспериментально был открыт английским ученым Р. Бойлем и французским ученым Э. Мариоттом. Поэтому он носит название закона Бойля-Мариотта.
Закон Бойля-Мариотта справедлив для любых газов, а также и для их смесей, например, для воздуха. Отклонения в законе наблюдаются только при очень высоких давлениях.
Реально провести изотермический процесс можно, медленно расширяя или сжимая газ, чтобы температура всей системы успевала выравниваться с температурой окружающей среды. (2)
Для газа постоянной массы и температуры произведение давления газа на его объем постоянно.
Этот закон экспериментально был открыт английским ученым Р. Бойлем и французским ученым Э. Мариоттом. Поэтому он носит название закона Бойля-Мариотта.
Закон Бойля-Мариотта справедлив для любых газов, а также и для их смесей, например, для воздуха. Отклонения в законе наблюдаются только при очень высоких давлениях.
Реально провести изотермический процесс можно, медленно расширяя или сжимая газ, чтобы температура всей системы успевала выравниваться с температурой окружающей среды.
| ||||
| Изотерма | Зависимость давления газа р от объема V при постоянной температуре графически изображается кривой, которая называется изотермой. Изотерма газа изображает обратно пропорциональную зависимость (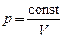 ). Кривую такого рода в математике называют гиперболой. ). Кривую такого рода в математике называют гиперболой.
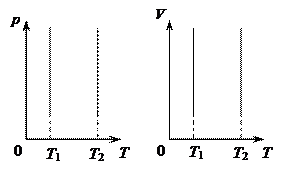 Разным постоянным температурам соответствуют разные изотермы. При повышении температуры давление, согласно уравнению состояния (1) увеличивается, если Разным постоянным температурам соответствуют разные изотермы. При повышении температуры давление, согласно уравнению состояния (1) увеличивается, если  . Поэтому изотерма, соответствующая более высокой температуре T2, лежит выше изотермы, соответствующей более низкой температуре T1. Ниже на рисунке показаны изотермы в осях (р, T) и (V, T). . Поэтому изотерма, соответствующая более высокой температуре T2, лежит выше изотермы, соответствующей более низкой температуре T1. Ниже на рисунке показаны изотермы в осях (р, T) и (V, T).

| ||||
| Изобарный процесс | Процесс изменения состояния газа при постоянной массе ( ) и постоянном давлении ( ) и постоянном давлении ( ) называют изобарным. Согласно уравнению (1) изобарный процесс имеет вид: ) называют изобарным. Согласно уравнению (1) изобарный процесс имеет вид:
 (3)
Для газа постоянной массы и постоянного давления отношение объема к температуре постоянно.
Этот закон был установлен экспериментально французским ученым Ж. Гей-Люссаком и носит название закона Гей-Люссака. Этот закон применим для газов и смесей газов.
Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается внешним давлением. (3)
Для газа постоянной массы и постоянного давления отношение объема к температуре постоянно.
Этот закон был установлен экспериментально французским ученым Ж. Гей-Люссаком и носит название закона Гей-Люссака. Этот закон применим для газов и смесей газов.
Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается внешним давлением.
| ||||
| Изобара | Согласно уравнению (3) объем газа линейно зависит от температуры при постоянном давлении:
 .
Эта зависимость графически изображается прямой, которая называется изобарой. .
Эта зависимость графически изображается прямой, которая называется изобарой.
 Различным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре согласно уравнению состояния (1) уменьшается. Поэтому изобара, соответствующая более высокому давлению р2, лежит ниже изобары, соответствующей более низкому давлению р1. Ниже на рисунке показаны изобары в осях (p, V) и (p, T). Различным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре согласно уравнению состояния (1) уменьшается. Поэтому изобара, соответствующая более высокому давлению р2, лежит ниже изобары, соответствующей более низкому давлению р1. Ниже на рисунке показаны изобары в осях (p, V) и (p, T).

| ||||
| Изохорный процесс | Процесс изменения состояния газа при постоянной массе ( ) и постоянном объеме ( ) и постоянном объеме ( ) называют изохорным.
Из уравнения состояния (1) вытекает изохорный процесс: ) называют изохорным.
Из уравнения состояния (1) вытекает изохорный процесс:
 (4)
Для газа постоянной массы и постоянного объема отношение давления к температуре постоянно.
Этот газовый закон был установлен французским физиком Ж. Шарлем и носит название закона Шарля. (4)
Для газа постоянной массы и постоянного объема отношение давления к температуре постоянно.
Этот газовый закон был установлен французским физиком Ж. Шарлем и носит название закона Шарля.
| ||||
| Изохора | Согласно уравнению (4) давление газа линейно зависит от температуры при постоянном объеме.
 .
Эта зависимость изображается прямой, называемой изохорой. Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно уравнению состояния (1) падает.
Поэтому изохора, соответствующая большему объему V2, лежит ниже изохоры, соответствующей меньшему объему V1.
Справа на рисунках показаны изохоры в осях (p, V) и (V, T). .
Эта зависимость изображается прямой, называемой изохорой. Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно уравнению состояния (1) падает.
Поэтому изохора, соответствующая большему объему V2, лежит ниже изохоры, соответствующей меньшему объему V1.
Справа на рисунках показаны изохоры в осях (p, V) и (V, T).
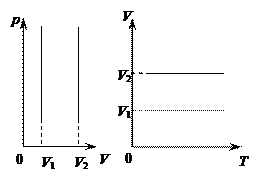

| ||||
| Определение внутренней энергии | Внутренней энергией тела называется сумма кинетической энергии хаотического движения его молекул и потенциальной энергии их взаимодействия. | ||||
| Внутренняя энергия идеального газа | Внутренняя энергия идеального газа представляет собой только кинетическую энергию теплового движения молекул. Молекулы идеального газа не взаимодействуют друг с другом, кроме моментов непосредственного столкновения. | ||||
| Внутренняя энергия идеального одноатомного газа |  .
Внутренняя энергия идеального одноатомного газа прямо пропорциональна его абсолютной температуре. Учитывая уравнение состояния, внутреннюю энергию можно определять по формуле .
Внутренняя энергия идеального одноатомного газа прямо пропорциональна его абсолютной температуре. Учитывая уравнение состояния, внутреннюю энергию можно определять по формуле
 . .
| ||||
| Изменение внутренней энергии идеального одноатомного газа | Изменение внутренней энергии данной массы идеального газа происходит только при изменении его температуры:
 .
Внутренняя энергия идеального одноатомного газа изменяется при любом процессе кроме изотермического. .
Внутренняя энергия идеального одноатомного газа изменяется при любом процессе кроме изотермического.
| ||||
| Внутренняя энергия многоатомного идеального газа | Если газ двухатомный, то внутренняя энергия такого газа определяется по формуле:
 .
Если молекулы газа состоят из трех и более атомов, то внутренняя энергия определяется по формуле: .
Если молекулы газа состоят из трех и более атомов, то внутренняя энергия определяется по формуле:
 . .
| ||||
| Работа газа | Газ совершает работу только при изменении объема сосуда, в котором этот газ находится. Вычислим работу в зависимости от изменения объема на примере газа в цилиндре, закрытом поршнем.
Модуль силы, действующей со стороны газа на поршень, равен:
где Пусть газ расширяется, и поршень смещается в направлении силы на малое расстояние
Из рисунка видно, что произведение
Следовательно
Работа расширения газа в изобарном процессе равна произведению давления газа на изменение его объема. | ||||
| Знак работы газа | Работа положительна при расширении газа  , поскольку сила давления газа и перемещение поршня направлены одинаково. Если же газ сжимается , поскольку сила давления газа и перемещение поршня направлены одинаково. Если же газ сжимается  , то работа силы, с которой газ действует на поршень, отрицательная. , то работа силы, с которой газ действует на поршень, отрицательная.
| ||||
| Геометрическое истолкование работы | При постоянном давлении работа газа
 .
Построим график зависимости давления газа .
Построим график зависимости давления газа  от объема от объема 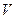 . .
 Здесь площадь прямоугольника АВСД, ограниченная графиком Здесь площадь прямоугольника АВСД, ограниченная графиком  , осью , осью  и отрезками АВ и СД, равными давлению газа, численно равна работе.
В общем случае при произвольном изменении объема газа давление не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему. и отрезками АВ и СД, равными давлению газа, численно равна работе.
В общем случае при произвольном изменении объема газа давление не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему.
 В этом случае для вычисления работы нужно общее изменение объема разделить на малые части, вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему будет численно равна площади фигуры, ограниченной графиком зависимости В этом случае для вычисления работы нужно общее изменение объема разделить на малые части, вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему будет численно равна площади фигуры, ограниченной графиком зависимости  от от 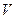 , осью , осью  и отрезками АВ и ДС, равными давлениям и отрезками АВ и ДС, равными давлениям  и и  в начальном и конечном состояниях. в начальном и конечном состояниях.
| ||||
| Закон сохранения энергии | На основании множества наблюдений и опытов был сформулирован закон сохранения энергии: энергия в природе не возникает из ничего и не исчезает: количество энергии неизменно, она только переходит из одной формы в другую. | ||||
| Первый закон термодинамики | Закон сохранения и превращения энергии, распространенный на тепловые явления, носит название первого закона термодинамики (первого начала термодинамики). Его суть заключается в следующем:
количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами:
  Часто вместо работы А тел системы рассматривают работу
Часто вместо работы А тел системы рассматривают работу  внешних тел над системой. Учитывая, что внешних тел над системой. Учитывая, что  , первый закон термодинамики можно сформулировать так: изменение внутренней энергии системы равно сумме сообщаемой ей количества теплоты и работы, произведенной над системой внешними силами: , первый закон термодинамики можно сформулировать так: изменение внутренней энергии системы равно сумме сообщаемой ей количества теплоты и работы, произведенной над системой внешними силами:  
| ||||
| Процесс | Изменение внутренней энергии:

| Работа газа:

| Количество теплоты:

| ||
| Изотермический | 
| 
| |||
| Изохорный |  (одноатомный газ)
(одноатомный газ)
| 
| |||
| Изобарный |  (одноатомный газ)
(одноатомный газ)
| 
| 
| ||
| Адиабатный | 
| 
| |||
| Адиабатный процесс | Адиабатным называется процесс, при котором не происходит теплообмена системы (газа) с окружающими телами. Таким образом, при адиабатном процессе  и согласно уравнению первого закона термодинамики, получаем: и согласно уравнению первого закона термодинамики, получаем:
 и и   При адиабатном процессе изменение внутренней энергии равно работе, выполняемой газом, но с противоположным знаком. Таким образом, адиабатное расширение ведет к понижению температуры газа, а адиабатное сжатие – к ее повышению.
При адиабатном процессе изменение внутренней энергии равно работе, выполняемой газом, но с противоположным знаком. Таким образом, адиабатное расширение ведет к понижению температуры газа, а адиабатное сжатие – к ее повышению.
| ||||
| Теплоемкость тела | Теплоемкостью тела называется произведение удельной теплоемкости вещества на массу тела:
 .
Теплоемкость тела С – это количество теплоты, которое нужно сообщить данному телу, чтобы повысить его температуру на 1ºС (К). Единицей измерения теплоемкости тела в системе СИ является .
Теплоемкость тела С – это количество теплоты, которое нужно сообщить данному телу, чтобы повысить его температуру на 1ºС (К). Единицей измерения теплоемкости тела в системе СИ является  . .
| ||||
Поиск по сайту:

 ,
, – площадь поверхности поршня.
– площадь поверхности поршня. . Если перемещение малое, то давление газа можно считать постоянным. Работа газа равна:
. Если перемещение малое, то давление газа можно считать постоянным. Работа газа равна: .
.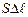 равно изменению объема газа от его первоначального значения
равно изменению объема газа от его первоначального значения  до конечного значения
до конечного значения  , т.е.
, т.е. .
. или
или