 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Лабораторна робота №5
Алгоритм Брезенхема для побудови кола
Мета роботи: освоїти побудову оціночних функцій для формування растрового представлення кола довільного радіуса, ознайомитись з основними етапами використання алгоритму Брезенхема для побудови кола
Постановка задачі
Дано: опис кола, який задано координатами центра кола (x1;y1) та довжиною радіуса R.
Необхідно: сформувати растрове представлення кола вказаного радіуса за допомогою алгоритму Брезенхема.
Теоретичні відомості
Існує декілька дуже простих, але не ефективних способів перетворення кіл в растрову форму. Наприклад, розглянемо для простоти коло з центром на початку координат. Її рівняння записується як x2 + y2 = R2. Вирішуючи це рівняння відносно в, отримаємо:
y = ± 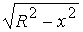 .
.
Щоб змалювати четвертую частину кола, будемо змінювати x з одиничним кроком від 0 до R і на кожному кроці обчислювати y. Другим простим методом растрової розгортки кола є використання обчислень x і y по формулах x = R cosα, y = R sinα при покроковій зміні кута α від 0° до 90°.
Для спрощення алгоритму растрової розгортки стандартного кола можна скористатися його симетрією відносно координатних осей і прямих y = ± x; у випадку, коли центр кола не збігається з початком координат, ці прямі необхідно посунути паралельно так, щоб вони пройшли через центр кола. Тим самим достатньо побудувати растрове зображення для 1/8 частини кола, а решту точок отримати симетрією (див. Рис. 3.1).
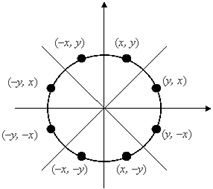
Рис. 3.1. Восьмистороння симетрія.
Розглянемо ділянку кола з другого октанта x Є [0, R/ 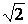 ]. Далі опишемо алгоритм Брезенхема для цієї ділянки кола. На кожному кроці алгоритм вибирає точку Pi (xi, yi), яка є найближчою до дійсного кола. Ідея алгоритму полягає у виборі найближчої точки за допомогою керуючих змінних, значення яких можна обчислити в покроковому режимі з використанням невеликого числа додавань, віднімань і зсувів.
]. Далі опишемо алгоритм Брезенхема для цієї ділянки кола. На кожному кроці алгоритм вибирає точку Pi (xi, yi), яка є найближчою до дійсного кола. Ідея алгоритму полягає у виборі найближчої точки за допомогою керуючих змінних, значення яких можна обчислити в покроковому режимі з використанням невеликого числа додавань, віднімань і зсувів.
Розглянемо невелику ділянку сітки пікселів, а також можливі способи (від т.A до т.E) проходження дійсного кола через сітку (Рис. 3.2). Припустимо, що точка P i-1 була вибрана як найближча до кола при x = x i-1. Тепер знайдемо, яка з точок (S i або T i) розташована ближче до кола при x = x i-1 + 1.

Рис. 3.2. Варіанти проходження кола через растрову сітку.
Причому похибка при виборі точки Pi (xi, yi) дорівнює:
D(Pi) = (xi 2 + yi 2) – R 2.
Запишемо вираз для похибок, які отримуються в результаті вибору точки Si або Ti:
D(Si) = [(xi-1+ 1)2 + (yi-1)2] – R2;
D(Ti) = [(xi-1+ 1)2 + (yi-1 – 1)2] – R 2.
Якщо | D(Si) | ≥ | D(Ti) |, то Ti ближче до реального кола, в іншому випадку - вибирається Si.
Введемо di = | D(Si) | – | D(Ti) |. Тоді Ti буде вбиратись при di ≥ 0, в іншому випадку буде виставлятись Si.
Далі запишемо di и di+ 1 для різних варіантів вибору точки Si або Ti.
D 1 = 3 – 2 R.
Якщо вибирається Si (коли di < 0), то di+ 1 = di + 4 xi-1 + 6.
Якщо вибирається Ti (коли di ≥ 0), то di+ 1 = di + 4 (xi- 1 – yi- 1) + 10.
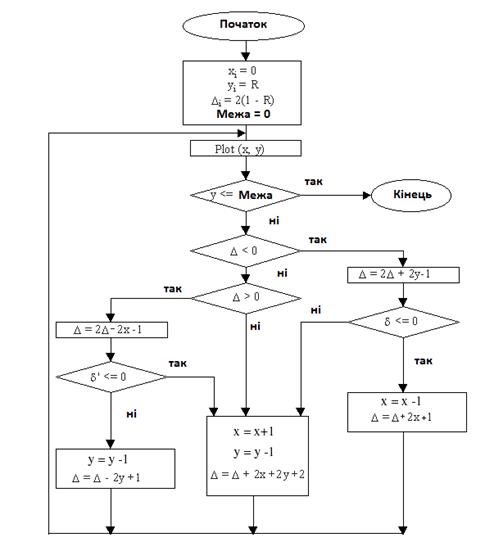
Рис. 3.3. Блок-схема алгоритму Брезенхема для побудови растрового представлення кола.
Варіанти завдань до лабораторної роботи
| Варіант | Завдання |
| Розробити програму зображення трьох кіл різних розмірів, розміщених один за одним в залежності від довжини радіуса | |
| Розробити програму зображення кола, радіус та центр якого задає користувач | |
| Розробити програму зображення м’яча, який рухається з лівого верхнього кута екрану у нижній правий | |
| Розробити програму зображення трьох кіл різних розмірів, розміщених один в одному в залежності від довжини радіуса | |
| Розробити програму зображення м’яча, який рухається з лівого нижнього кута екрану у верхній правий |
Контрольні питання
1. В чому полягає основна ідея алгоритму Брезенхема для побудови растрового представлення кола?
2. Описати графічно основну ідею алгоритму Брезенхема для побудови кола.
3. Які переваги та недоліки алгоритму Брезенхема для побудови кола?
4. Чи накопичується помилка в процесі виконання алгоритму Брезенхема?
5. Скільки пік селів на растровому зображенні кола необхідно для обчислення його радіуса? Яка точність обрахунку радіуса?
6. Описати етапи виконання алгоритму Брезенхема для побудови кола.
Література
1. Роджерс Д.Алгоритмы машинной графики/ Д. Роджерс. – М.: Мир, 1989. – 230 с.
2. Фоли Дж., А. вэн Дэм Основы интерактивной машинной графики. – М.: Мир, 1985, том2. – 287 с.
Поиск по сайту: