Целевая функция

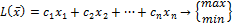(1)

Ограничения

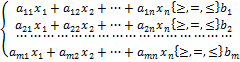(2)

Прямое ограничение переменных (например, условие неотрицательности)

(3)

При этом a_ji, b_j, c_i (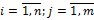) заданные постоянные величины.

Задача состоит в нахождении оптимального значения функции (.1) при соблюдении ограничений (2) и (3).

Систему ограничений (2) называют функциональными ограничениями задачи, а ограничения (3) - прямыми.

Вектор 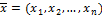, удовлетворяющий ограничениям (2) и (3), называется допустимым решением (опорным планом) задачи линейного программирования. План , при котором функция (1) достигает своего максимального (минимального) значения, называется оптимальным.

Задача 1. Планирование выпуска продукции пошивочного предприятия.

Планируется выпуск мужских и женских костюмов. На один женский костюм потребуется 2м шерстяной ткани, 1 м вельвета, 0,5 м джерси и 1,5 человекодня трудовых затрат. На один мужской костюм 2,5 м шерстяной ткани, 1 м джерси и 1 человекодень трудовых затрат. Всего на предприятии имеется в наличии 350 м шерсти, 120 м джерси, 100 м вельвета и 450 человекодней трудозатрат. Требуется определить, сколько надо произвести каждого вида костюмов, чтобы прибыль была максимальной, учитывая, что прибыль от одного женского костюма – 700 руб., а от мужского – 500 руб. При этом надо иметь в виду, что на поставку мужских костюмов заключен договор на количество 40 шт.

Решение.

Искомым решением в данной задаче является количество костюмов каждого вида, которое нам необходимо производить исходя из имеющегося сырья и трудовых ресурсов. Это и будут наши неизвестные переменные. Введем обозначения х₁ – количество штук женских костюмов; х₂ – количество штук мужских костюмов. Тогда целевая функция, которая должна вычислять общую прибыль запишется следующим образом:

F=700x₁+500x₂→max

Составляются ограничения по ресурсам.

Расход шерсти 2x₁+2,5x₂≤350

Расход джерси 0,5x₁ + x₂≤120

Расход вельвета x₁ ≤ 100 (4)

Трудовые затраты 1,5x₁ + x₂≤450

x₁ ≥0

x₂ ≥0

Для решения задачи подготовим исходные данные и формулы, описывающие математическую модель (4) на рабочем листе MS Excel (рис. 1).

Рисунок 1 – Исходные данные задачи

На рисунке 1 в ячейку D5 внесена формула =СУММПРОИЗВ($B$4:$C$4;B5:C5), которая реализует левую часть первого ограничения. Затем она копируется вниз до ячейки D9. В ячейках B4:C4 (выделены зеленым цветом) занесены начальные значения искомых переменных, равные 0. В формуле эти ячейки используются в абсолютной адресации, т.е. со знаком доллара. Это делается для того, чтобы формулу можно было скопировать вниз с помощью инструмента растягивания. В ячейке D9 (выделена красным цветом) будет вычисляться целевая функция. Левые части ограничений (выделены синим цветом) ячейки D5:D8 будут в ходе решения вычисляться и сравниваться с правыми частями ограничений, ячейками Е5:Е8.

Исходные данные модели готовы. Открываем окно поиска решения Данные – Поиск решения.

Если на ленте Данные поиск решения отсутствует, то выполните следующий порядок действий. Конпка Office (верхний левый угол) – Параметры – Надстройки – Перейти – Поставить галочку на Поиск решения – ОК.

В окне поиска решения установить в качестве целевой ячейки D9, поиск на максимум, в качестве изменяемых ячеек – B4:C4 (ячейки переменных). С помощью кнопки Добавить введите друг за другом ограничения в соответствии с рисунком 2.

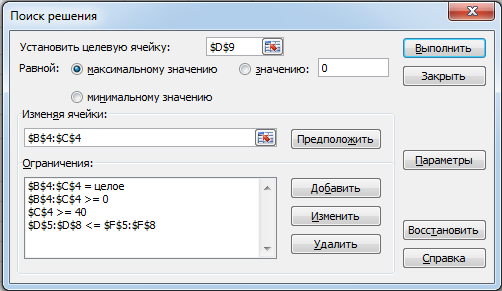
Рисунок 2 – Окно поиска решения для задачи 1.

Обратите внимание, что если ограничения одного типа, то их можно вводить блоками. После заполнения нажать Выполнить. В случае успешного решения будет выведено информационное окно (рис. 3), в котором можно сформировать 3 отчета. Эти отчеты понадобятся нам для анализа решения. А в самой таблице мы теперь можем видеть оптимальное решение (рис. 4), в соответствии с которым нам выгодно производить 100 женских костюмов и 60 мужских. При это, максимальная прибыль составит 100000 руб. Как видно из решения у нас остаются излишки ткани джерси 10 м и очень много лишних трудовых ресурсов. Следовательно, придется либо сокращать людей, либо искать дополнительное сырье и рынки сбыта готовой продукции.

Рисунок 3 – Информационное окно Поиска решения

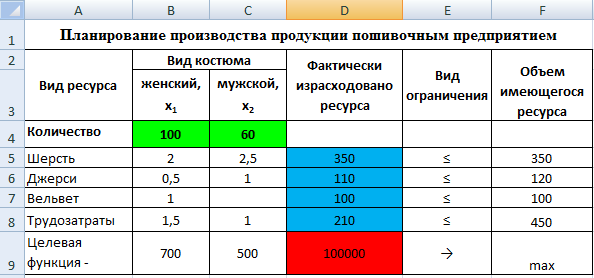
Рисунок 4 – Результат решения

Предположим, что мы не хотим проводить сокращение штата. Тогда нам необходимо знать, сколько ресурсов других видов надо дополнительно приобрести и сколько костюмов будет дополнительно изготовлено. Учитывая последнее, попробуйте, меняя значения в ячейках B4:C4, подобрать такие значения, чтобы трудовые ресурсы использовались полностью. Замените правые части ограничений соответствующими значениями и прорешайте задачу еще раз. Результат представлен на рисунке 5. Нам необходимо дополнительно приобрести 443 м шерстяной ткани, 140 м джерси и 90 м вельвета. Тогда все рабочие будут заняты и мы произведем дополнительно 90 шт. женских костюмов и 105 шт. мужских. Получим прибыль в размере 215500 руб.

Рисунок 5 – Второй вариант решения задачи 1

Поиск по сайту: