Приёмы выполнений тождественных преобразований

При выполнении тождественных преобразований алгебраических выражений необходимо знать порядок выполнения действий, действия с дробями и степенными выражениями, формулы сокращенного умножения и др.

Следует иметь в виду, что при тождественных преобразованиях остаются неизменными:

- величина допустимых изменений буквенных величин;

- область допустимых значений каждой из буквенных величин.

Первое из этих требований является обязательным при всех преобразованиях, имеющих целью упрощение выражения или приведение его к нужному виду. Если надо, например, дополнить квадратный трехчлен 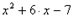до полного квадрата, то, прибавив к нему число 9, необходимо такое же число и вычесть, т.е.

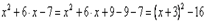Тождественные преобразования последнего выражения можно продолжить и привести исходное выражение к произведению двучленов:

Второе требование – неизменность областей допустимых значений, не всегда выполняется при обычно применяемых нами преобразованиях. Сократив, например, дробь на разность 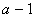и написав равенство 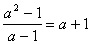, мы замечаем, что нарушено второе требование, которому должно удовлетворять тождественное преобразование: правая часть равенства имеет смысл при любых значениях 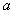, а левая только при условии, что , т.е. произошло изменение области допустимых значений величины 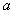. Следовательно, преобразование в данном случае не является тождественным.

Однако это не значит, что мы должны отказываться от таких преобразований, которые изменяют области допустимых значений величин. Напротив, мы ими часто пользуемся и при упрощении выражений и при решении уравнений. Нужно только при каждом таком преобразовании указать, как изменились области допустимых значений буквенных величин.

№33 Теорема, структура теоремы, виды теорем (примеры)

Структуру отдельных мыслей и способы их сочетаний называют формами мышления. С точки зрения формальной логики мышление характеризуется 3 основными формами: понятиями, суждениями, умозаключениями.

Пример понятия. Треугольник – это фигура, состоящая из 3 отрезков, попарно соединяющих 3 точки, не пересекающихся на одной прямой.

Пример суждения. Через любые две точки проходит прямая, и притом только одна.

Пример умозаключения. Если a>b, b>c, то a>c.

Математическое предложение, истинность которого устанавливается посредством доказательства – называется теоремой. Название «теорема» происходит от греческого слова τεορεμα – представление, зрелище. (т.к. в древности часто теоремы доказывались публично, на площадях, и они носили характер спора, дискуссии).

В школьном курсе математики для словесной формулировки теоремы используются три формы суждения:

1. Категорическая.

Пример.

Средняя линия трапеции параллельна основаниям и равна их полу сумме.

Постоянный множитель можно вынести за знак производной:

2. Условная.

Пример.

Если в треугольники два угла равны, то треугольник равнобедренный.

Если на некотором промежутке, то на этом промежутке F(x)=c, с – постоянная.

3. Разделительная

Пример.

Плоскость и не лежащая на ней прямая либо не пересекается, либо пересекается в одной точке.

Теоремы категорической и разделительной формы можно переформулировать в терминах «если…, то…», т.е. обратить ее формулировку в условную.

Пусть, например, дана теорема:

«В ромбе диагонали взаимно-перпендикулярны». В условной форме формулировка этой теоремы будет выглядеть так: «Если четырёхугольник является ромбом, то его диагонали взаимно-перпендикулярны». Заметим, что разбор структуры теоремы более доступен для учащихся, ели она сформулирована в условной форме. Условная форма теоремы м.б. эффективно использована и для того, чтобы дать ответ на вопрос: «о свойстве или о признаке идет речь в теореме?». На этот вопрос легко ответить, если теорему сформулировать в условной форме. Если окажется, что рассматриваемое понятие находится в условие теоремы, то теорема выражает свойство этого понятия, если же понятие находится в заключение теоремы, то она выражает признак.

В школьном курсе математики формулируются и доказываются теоремы, имеющие различный вид: в одних теоремах из одного условия вытекает одно заключение, в других – из одного условия вытекает несколько заключений, в третьих – из нескольких условий вытекает одно заключение и т.д.

В любом случае теорема состоит из трех частей:

1. Разъяснительная часть, в которой описывается множество М объектов, о которых идет речь в этой теореме.

2. Условие теоремы, то есть некоторый предикат А(х), заданный на множестве М.

3. Заключение теоремы – некоторый предикат В(х), заданный на том же множестве М.

В символах математической логики теорема м.б. записана следующим образом:

Часто в литературе используется такая терминология:

Тезис – доказываемое утверждение. Аргументы (основание доказательства)- используемые в доказательстве уже известные утверждения, из которых необходимо следует истинность доказываемого тезиса. Демонстрация – последовательность расположения аргументов и выводов, образующих цепь умозаключений. При доказательстве тезис должен удовлетворять следующим требованиям: быть ясным и точно определенным; оставаться тождественным, т.е. одним и тем же на протяжении всего доказательства; не должен содержать в себе логического противоречия; не должен находиться в логическом противоречии с суждениями по данному вопросу, высказанными ранее. Требования к аргументам доказательства таковы: они должны быть истинным предложением данной теории; быть достаточным основанием для доказываемого предложения; истинность которого доказана самостоятельно, независимо от доказываемого предложения.

С любой теоремой связаны еще три теоремы.

Четыре вида теорем:

1. – прямая теорема.

2. – обратная теорема.

3. – противоположная теорема.

4. – обратная к противоположной теорема (контрапозитивная).

Пример:

1. Если 4 – угольник параллелограмм, то диагонали его, пересекаясь, делятся пополам (истинно).

2. Если в 4 - угольнике диагонали пересекаясь, делятся пополам, то этот 4 – угольник – параллелограмм (истинно).

3. Если 4 – угольник не параллелограмм, то его диагонали, пересекаясь, не делятся пополам (истинно).

4. Если в 4 – угольнике диагонали пересекаясь, не делятся пополам, то такой 4 – угольник не параллелограмм (истинно).

Пример:

1. Если углы вертикальны, то они равны (И).

2. Если углы равны, то они вертикальны (Л).

3. Если углы не вертикальны, то они не равны (Л).

4. Если углы не равны, то они не вертикальные (И).

Прямая и обратная к противоположной теореме эквивалентны, т.е. они одновременно истинны или ложны. Обратная теорема и противоположная теорема эквивалентны, т.е. одновременно истинны или ложны. Такая связь м/у теоремами показывает нецелесообразность изучения всех четырех теорем, достаточно установить истинность или ложность одной какой – либо логически неравносильной пары теорем (1 и 2) или (3 и 4), т.к. истинность или ложность одной такой пары влечет за собой истинность или ложность другой пары теорем.

В связи с этим, в любом курсе математики встречаются лишь прямая и обратная теоремы.

Поиск по сайту: