 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Использование интегрирующего множителя
Числовые ряды. Сходимость ряда. Необходимый признак сходимости ряда.
Сумма числового ряда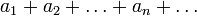 
определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда 
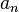представляют собой комплексные числа (в частности, вещественные).
Пусть 
— числовой ряд. Число 
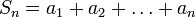называется n -ой частичной суммой ряда 
.
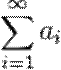Сумма (числового) ряда — это предел частичных сумм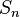 
, если он существует и конечен. Таким образом, если существует число 
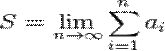, то в этом случае пишут 
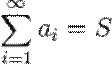. Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.
Свойство 1. Если ряд
(1.1)
сходится и его сумма равна S, то ряд
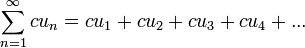(1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд (1.2) расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
,
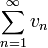а их суммы равны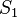 
и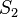 
соответственно, то сходятся и ряды
,
причём сумма каждого равна соответственно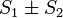 
.
Ряд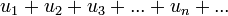 
может сходиться лишь в том случае, когда член 
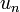(общий член ряда) стремится к нулю:
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
Линейные ДУ 1-го порядка
Дифференциальное уравнение вида
где a (x) и b (x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Рассмотрим два метода решения указанных уравнений:
- Использование интегрирующего множителя;
- Метод вариации постоянной.
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
то интегрирующий множитель определяется формулой:
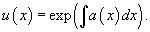
Умножение левой части уравнения на интегрирующий множитель u (x) преобразует ее в производную произведения y (x) u (x).
Общее решение диффференциального уравнения выражается в виде:
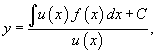
где C − произвольная постоянная.
Поиск по сайту: