Методические указания. Структурная схема надежности заданного варианта получается из схемы надежности, приведенной на рис.3

Структурная схема надежности заданного варианта получается из схемы надежности, приведенной на рис.3, путем исключения двух элементов, номера которых указаны в таблице 2. Полученную структуру следует изобразить, отметив ее вход и выход.

Алгоритм расчета надежности такой сложной структуры сводится к следующему [3]:

1. Производится поэтапное эквивалентирование структуры объединением последовательно и параллельно соединенных элементов.

При последовательном соединении элементов:

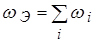, 1/год;

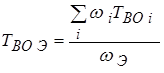, час; (16)

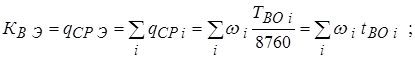
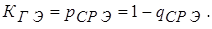
Здесь 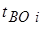- среднее время восстановления i-го элемента системы, выраженное в годах.

При параллельном соединении двух элементов:

, час;

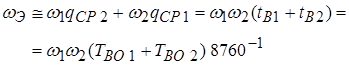, 1/год. (17)

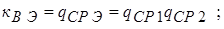
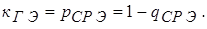
При параллельном соединении n элементов:

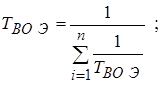
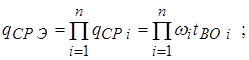(18)

1/год.

Для трех параллельно соединенных элементов из (18) получаем:

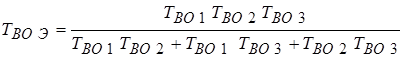, час (19)

1/год.

В результате эквивалентирования для такой структуры образуется двухполюсный связный неразделимый граф. Проверяется, может ли надежность системы быть определена по надежности ее минимальных сечений, т.е. соблюдается ли неравенство:

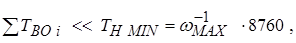
здесь 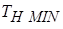- среднее время безотказной работы наименее надежного элемента, выраженное в часах.

2. Определяется совокупность минимальных сечений, образованная этим графом. Алгоритм определения минимальных сечений состоит в следующем.

2.1. Составляется матрица непосредственных связей вершин и ребер графа (см. примеры 3.7 и 3.8 в [3]). Ориентированные ребра (ребра с заданным направлением), которые входят в вершину, отмечаются знаком " - "; ребра с заданным направлением, которые выходят из вершины, как и неориентированные ребра – знаком " + ".

2.2. Составляется массив N – деревьев графа последовательным присоединением к

N _i-1 – дереву вершин, непосредственно связанных с одной из вершин, уже принадлежащих N _i-1 – дереву. Нельзя присоединять только одну вершину – выход графа, так как иначе образовалась бы связанная структура.

2.3. Для каждого N _i – дерева определяются сечения. По матрице ребра-вершины в столбик выписываются все ребра, непосредственно связанные с вершинами N деревьев (табл. 3.5 в [3]). В столбце "ребра" таблицы, ребра, входящие в совокупность ребер N дерева четное число раз, независимо от присвоенного им знака, вычеркиваются, кроме того, вычеркиваются также ребра, входящие в совокупность ребер N дерева со знаком "–". Оставшиеся ребра выписываются в столбец "сечения".

2.4. Выбираются минимальные сечения из множества полученных сечений. Для этого все сечения представляются в порядке возрастания числа элементов и уточняется, не содержатся ли в сечениях с большим числом элементов сечения с меньшим числом элементов. Если содержатся, то сечения с большим числом элементов исключаются. Оставшиеся сечения являются минимальными.

3. Находятся показатели надежности сечений (как для параллельно соединенных элементов) и показатели надежности всей системы по последовательно соединенным минимальным сечениям.

Среднее время безотказной работы системы:

, лет.

Вероятность отказа системы за год (t= 1 год):

.

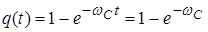Задание 3

От трансформаторной подстанции на промышленном предприятии получают электроэнергию четыре участка цеха. Законы распределения случайных величин – нагрузок участков нормальные с параметрами m₁…m₄, s₁…s₄.

Корреляционная связь между случайными величинами /нагрузками участков/ характеризуется матрицей коэффициентов корреляции .

Требуется:

1. Определить максимальные активные мощности участков, вероятность превышения которых g.

2. Определить максимальную активную мощность трансформаторной подстанции, вероятность превышения которой g, учтя, что закон распределения мощности подстанции также нормальный.

3. Сравнить максимальную мощность подстанции с суммой максимальных мощностей участков. Как изменится соотношение между этими мощностями, если считать, что корреляционная связь между нагрузками участков отсутствует?

4. Определить вероятность нахождения значений активной мощности в заданном интервале мощностей.

Предварительно следует рассмотреть методику решения задач 7.3, 8.5 по [4 ].

Таблица 4 Исходные данные к заданию №3

№ вар- та	т1, кВт	m2, кВт	m3, кВт	m4, кВт	s1, кВт	s2, кВт	s3, кВт	s4, кВт	№ мат- рицы	g	Интервал Р, кВт
										0,0062	4000…6000
										0,05	4000…6000
										0,00135	4000…6000
										0,0062	5000…7000
										0,05	4500…6500
										0,00135	5000…7000
										0,0062	4000…5500
										0,05	4800…6800
										0,0035	4300…6300
										0,0062	5000…6800
										0,05	4500…6500
										0,05	4600…6600
										0,05	4700…6700
										0,0062	4800…6800
										0,00135	4900…6900
										0,0062	5000…7000
										0,05	5000…7000
										0,05	5200…7100
										0,062	5100…7200
										0,0062	5300…7500
										0,00135	5500…7500
										0,05	5000…7000
										0,0062	5700…7500
										0,05	5500…7300
										0,0062	4000…6000
										0,05	4000…6000
										0,00135	4000…6000
										0,0062	5000…7000
										0,05	4500…6500
										0,00135	5000…7000
										0,0062	4000…5500
										0,05	4800…6800
										0,0035	4300…6300
										0,0062	5000…6800
										0,05	4500…6500
										0,05	4600…6600
										0,05	4700…6700
										0,0062	4800…6800
										0,00135	4900…6900
										0,0062	5000…7000
										0,05	5000…7000
										0,05	5200…7100
										0,062	5100…7200
										0,0062	5300…7500
										0,00135	5500…7500
										0,05	5000…7000
										0,0062	5700…7500
										0,05	5500…7300
										0,0062	4800…6700
										0,05	4500…6500

Матрицы коэффициентов корреляции:

1. ;

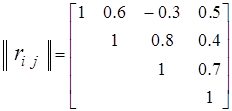2. .

Литература

1. Идельчик В.И. Электрические системы и сети. – М.: Энергоатомиздат, 1989. – 542 с.

2. Электроэнергетические системы в примерах и иллюстрациях /Под ред. В.А.Веникова. – М.: Энергоиздат, 1983. – 504 с.

3. Надежность систем электроснабжения /В.В.Зорин и др. – К.: Выща шк., 1984. – 192 с.

4. Расчеты и анализ режимов работы сетей /Под ред. В.А.Веникова. – М.: Энергия, 1974. – 336 с.

Поиск по сайту: