 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формирование системы нелинейных уравнений узловых напряжений в форме баланса мощностей
Перед формированием системы уравнений узловых напряжений в форме баланса мощностей следует преобразовать схему замещения, приведенную в задании, сведя ее к схеме с двумя независимыми узлами.
4.1. Алгоритм преобразования схемы замещения 1.
4.1.1. Разносим нагрузку узла 2 в узлы 1 и 3
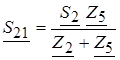 ,
,  .
.
Проверка:  .
.
4.1.2. Рассчитываем значения мощностей нагрузок в узлах 1 и 3 с учетом нагрузки узла 2:
 ;
; 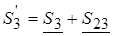 .
.
4.1.3. Складываем последовательно ветви 2 и 5:  ; находим проводимость эквивалентной ветви 2-5
; находим проводимость эквивалентной ветви 2-5  и результирующую проводимость между узлами 1 и 3:
и результирующую проводимость между узлами 1 и 3:  .
.
4.1.4. Переименовываем: узел 3 в узел 2, узел 4 в узел 3, ветвь 4 в ветвь 3, а эквивалентную ветвь между узлами 1 и 3 в ветвь 2 (см. рис.2). Тогда на рис.2  ;
; 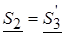 ;
;  (по таблице исходных данных);
(по таблице исходных данных);  ;
;  , а
, а 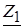 берется по таблице исходных данных.
берется по таблице исходных данных.
4.2. Алгоритм преобразования схемы замещения 2.
4.2.1. Разносим нагрузку узла 3 в узлы 2 и 4
 ,
,  .
.
Проверка: 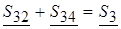 .
.
4.2.2. Рассчитываем значение мощности нагрузки в узле 2:  .
.
4.2.3. Складываем последовательно ветви 4 и 5:  ; находим проводимость эквивалентной ветви 4-5
; находим проводимость эквивалентной ветви 4-5 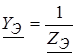 и результирующую проводимость между узлами 2 и 4:
и результирующую проводимость между узлами 2 и 4:  .
.
4.2.4. Переименовываем: узел 4 в узел 3, назовем эквивалентную ветвь между узлами 2 и 4 ветвью 3. Тогда на рис.2 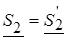 ,
,  (по таблице исходных данных),
(по таблице исходных данных), 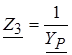 ,
,  ,
, 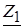 и
и 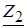 соответствуют исходным данным задания для мощности и сопротивлений с указанными индексами.
соответствуют исходным данным задания для мощности и сопротивлений с указанными индексами.
|



|
|



|
|











Рисунок 2. Преобразованная схема замещения
4.3. Система нелинейных алгебраических уравнений узловых напряжений в форме баланса мощностей, записанная в выражениях для небалансов мощностей в узлах, имеет вид:
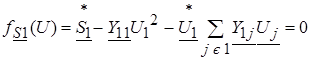 ;
;
……………………………………….
 ; (7)
; (7)
……………………………………….
 .
.
Здесь  - сумма для всех узлов j, связанных с узлом k (куст узла k).
- сумма для всех узлов j, связанных с узлом k (куст узла k).
Если в качестве неизвестных при решении уравнений (7) используются модули и фазы напряжений в узлах 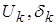 , то после выражения
, то после выражения 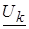 через
через  и
и 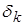 , k=1…n,
, k=1…n,
подстановки в (7) активных и реактивных составляющих проводимостей узлов, активных и реактивных мощностей в узлах, напряжения базисного узла и приравняв нулю отдельно действительные и мнимые части комплексов, получаем систему трансцендентных уравнений узловых напряжений в форме баланса мощностей при неизвестных  . Для к-го узла, уравнение узловых напряжений, записанное в виде функций небалансов активных и реактивных мощностей в узле, имеет вид:
. Для к-го узла, уравнение узловых напряжений, записанное в виде функций небалансов активных и реактивных мощностей в узле, имеет вид: 

 (8)
(8)
где 

Для схемы замещения, представленной на рис.2, система уравнений (8) имеет следующий вид:
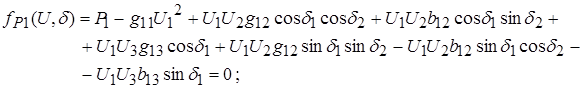
 (9)
(9)


Для формирования системы уравнений (9) следует по схеме замещения рис.2 рассчитать элементы матриц активных и реактивных составляющих узловых проводимостей, воспользовавшись приведенными выше рекомендациями и результатами расчетов, выполненных в соответствии с п.1 и п.п.4.1 и 4.2 курсовой работы. Следует проверить правильность расчетов элементов матриц Gу и Bу, воспользовавшись программой ZEIDEL. Для входа в программу необходимо запустить на выполнение файл start.bat. В режиме диалога следует ввести информацию о схеме замещения рис.2: число узлов N=3, базисный узел Nб=3, базисное напряжение Uб – согласно исходным данным, число ветвей М=3.
Рассчитанные численные значения элементов матриц Gу и Bу, См, значения активных Р, МВти реактивных Q, Мвармощностей в узлах, напряжение базисного узла U3 , кВследует подставить в систему (9).
Внимание! В систему уравнений (9) в отличие от систем (4) и (6) все проводимости 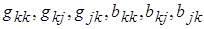 следует подставлять со знаком плюс, все мощности нагрузок в узлах
следует подставлять со знаком плюс, все мощности нагрузок в узлах 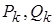 , как и ранее, со знаком минус.
, как и ранее, со знаком минус.
5. Решение системы нелинейных уравнений узловых напряжений в форме баланса мощностей методом Ньютона.
Решение системы трансцендентных уравнений (9) методом Ньютона предусматривает итерационный процесс, на каждом р-м шаге которого, р= 1,2 … решается относительно поправок  к искомым неизвестным линеаризованная система уравнений (10). В системе (10) слева находится квадратная матрица первых производных функций небалансов мощностей в узлах по модулям и фазам неизвестных напряжений U 1, U 2(матрица Якоби). Решение системы линейных алгебраических уравнений (10) методом Гаусса позволяет получить новые (уточненные) значения искомых неизвестных по формулам (11). Итерационный процесс продолжается до тех пор, пока небалансы (невязки) в (9) не станут меньше требуемой точности e, например e = 0,01МВт, Мвар.
к искомым неизвестным линеаризованная система уравнений (10). В системе (10) слева находится квадратная матрица первых производных функций небалансов мощностей в узлах по модулям и фазам неизвестных напряжений U 1, U 2(матрица Якоби). Решение системы линейных алгебраических уравнений (10) методом Гаусса позволяет получить новые (уточненные) значения искомых неизвестных по формулам (11). Итерационный процесс продолжается до тех пор, пока небалансы (невязки) в (9) не станут меньше требуемой точности e, например e = 0,01МВт, Мвар.
Для формирования линеаризованной системы уравнений (10) необходимо получить выражения для первых производных функций небалансов активных и реактивных мощностей в узлах по модулям и фазам неизвестных напряжений. Эти выражения получаются в таком виде:



 (10)
(10)

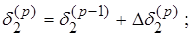 (11)
(11)
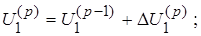
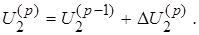

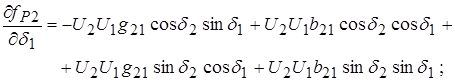
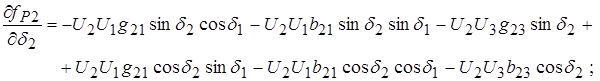



 (12)
(12)


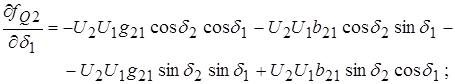
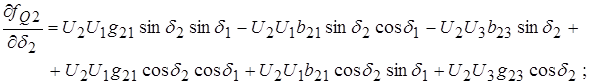


В эти выражения следует подставлять найденные численные значения активных и реактивных составляющих узловых проводимостей, помня о замечании, приведенном в п.4.3.
Порядок итерационного расчета:
1. Задаемся начальным (нулевым) приближением неизвестных. Рекомендуется принять  .
.
2. Рассчитываем небалансы активных и реактивных мощностей на нулевом шаге  (правые части в системе 10) согласно (9) и сравниваем их с заданной точностью. Если требуемая точность достигнута – конец расчета, если нет – идти к п.3.
(правые части в системе 10) согласно (9) и сравниваем их с заданной точностью. Если требуемая точность достигнута – конец расчета, если нет – идти к п.3.
3. Подставляем начальные приближения неизвестных в выражения (12) для производных и рассчитываем нулевое приближение элементов матрицы Якоби. На этом заканчивается формирование линеаризованной системы уравнений. Ее следует записать в матричной форме (10).
4. Решаем систему уравнений (10) на компьютере по программе C:\STUDENT\MAT_ZAD\LIN_UR. Находим первое приближение поправок  и неизвестных
и неизвестных  согласно (11). Далее следует идти к п.2, т.е. рассчитать небалансы P и Q на первом шаге, подставив в (9) первое приближение неизвестных, и сравнить их с требуемой точностью. Если она не достигнута, выполняется п.3 алгоритма, т.е. первое приближение неизвестных подставляем в выражение (12) для производных и рассчитываем новые значения элементов матрицы Якоби.
согласно (11). Далее следует идти к п.2, т.е. рассчитать небалансы P и Q на первом шаге, подставив в (9) первое приближение неизвестных, и сравнить их с требуемой точностью. Если она не достигнута, выполняется п.3 алгоритма, т.е. первое приближение неизвестных подставляем в выражение (12) для производных и рассчитываем новые значения элементов матрицы Якоби.
Далее выполняем п.4 алгоритма, находим второе приближение поправок и неизвестных  ,
, 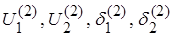 и переходим к п.2. После расчета небалансов закончить итерационный процесс.
и переходим к п.2. После расчета небалансов закончить итерационный процесс.
Рассчитанные напряжения следует сопоставить с найденными на компьютере по программам GAUSSи ZEIDELи сделать выводы о величинах погрешностей. Следует оценить также значения небалансов P и Q в узлах после выполнения шагов метода Ньютона. На этом расчет напряжений в узлах заканчивается.
Поиск по сайту: