Решение системы нелинейных уравнений узловых напряжений в форме баланса токов с использованием метода Гаусса на каждом шаге итерационного процесса (внешней итерации)

Одесский Национальный политехнический университет

Кафедра электроснабжения

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К курсовой работе

По дисциплине

"МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ЭНЕРГЕТИКИ"

Составили: к.т.н., доцент Невольниченко В.Н.,

к.т.н., доцент. Бесараб А.Н.

Одесса 2005

Введение

Дисциплина "Математические задачи энергетики" является промежуточной между курсами общей и прикладной математики и теоретических основ электротехники с одной стороны и дисциплинами специализации с другой.

Цель изучения дисциплины – связать указанные общетеоретические дисциплины с практическими их применениями в работе специалиста и получить конкретный математический аппарат для исследований систем электроснабжения. Содержание дисциплины ориентировано на наиболее характерные задачи анализа систем электроснабжения: расчеты установившихся режимов, количественную оценку надежности энергетических объектов и систем, прогнозирование спроса мощности и энергии в системе и отдельными потребителями, расчет электрических нагрузок. Рассматриваются методы и алгоритмы, большая часть из которых реализуется в виде программ для компьютеров.

Изучение данной дисциплины требует соответствующей подготовки студентов по математике и теоретическим основам электротехники. Из математики особенно важны разделы матричной алгебры, алгебры комплексных чисел, методов решения систем алгебраических уравнений, основ теории вероятностей и математической статистики. Из курса теоретических основ электротехники в первую очередь необходимы знания по основам теории цепей.

В курсовой работе решаются задачи по основным разделам дисциплины:

· математическим основам методов анализа установившихся режимов электроэнергетических систем (задание 1);

· количественной оценке надежности сложных структур (задание 2);

· расчетам характеристик режима с использованием модели систем случайных величин (задание 3).

Содержание указанных заданий ориентировано на вычисления с помощью простейших расчетных средств и только в отдельных случаях требуется применение компьютера.

Задание 1

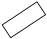
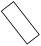
От центра питания А (узел 4) по замкнутой сети, схема замещения которой приведена на рисунке1, получают электроэнергию подстанции, подключаемые к узлам 1, 2, 3. Напряжение центра питания U­₄, сопротивления участков сети Z_j, j = 1…5 и расчетные нагрузки подстанций S_i, i = 1, 2, 3 даны в таблице 1.

				1.				2.
	A (4)				A (4)

Рисунок 1 Схемы замещения замкнутой сети

Требуется рассчитать установившийся режим для заданного участка сети, т.е. определить напряжения в точках присоединения нагрузок, токи ветвей, мощности в начале и в конце каждой ветви и суммарные потери мощности в сети. Задачу следует решить методом узловых напряжений.

Напряжения в узлах следует определить тремя способами:

1. Сформировать систему нелинейных уравнений узловых напряжений в форме баланса токов при неизвестных действительных и мнимых составляющих напряжений и решить ее двумя способами:

1.1 линеаризовать систему уравнений на каждом шаге итерационного процесса (внешняя итерация) и использовать для решения линеаризованных уравнений алгоритм Гаусса с обратным ходом (выполнить два шага внешней итерации);

1.2 использовать алгоритм Гаусса-Зейделя для решения систем нелинейных алгебраических уравнений.

2. Сформировать систему трансцендентных уравнений узловых напряжений в форме баланса мощностей при неизвестных модулях и фазах напряжений узлов U_k, d_k и решить ее методом Ньютона-Рафсона (выполнить два шага итерационного процесса). Предварительно из-за трудоемкости вычисления элементов матрицы производных следует преобразовать схему замещения: разнести нагрузку узла 2 для вариантов заданий со схемой 1, и узла 3 для вариантов заданий со схемой 2 в соседние узлы и сложить последовательные и параллельные ветви.

Таблица 1 Данные элементов системы к заданию 1

Фазовые углы комплексов сопротивлений:

j_Z1 = 50°; j_Z2 = 48°; j_Z3 = 64°; j_Z4 = 30°; j_Z5 = 70°.

Фазовые углы комплексов мощностей:

j_S1 = 50°; j_S2 = 48°; j_S3 = 64°.

1. Формирование системы нелинейных алгебраических уравнений узловых напряжений в форме баланса токов.

где Yу – комплексная матрица узловых проводимостей порядка n, где n – число независимых узлов (в задании n=3),

Uу – матрица-столбец неизвестных междуфазных напряжений узлов,

J (Uу) – матрица-столбец нелинейных задающих токов, зависящих от напряжений; каждый элемент этой матрицы J _k(U _k) = _k / _k , где _k – сопряженный комплекс заданной мощности трех фаз k -го узла (для генераторных узлов со знаком плюс, для нагрузочных – со знаком минус), _k – сопряженный комплекс междуфазного напряжения k -го узла,

Yб – матрица-столбец взаимных проводимостей ветвей между балансирующим и остальными узлами; если узел k не связан с балансирующим (отсутствует связывающая эти узлы ветвь), то Ykб = 0.

Uб – междуфазное напряжение базисного узла, совпадающего с балансирующим (в задании это узел 4); как правило, вектор напряжения базисного узла ориентируют вдоль положительного направления действительной оси комплексной плоскости, поэтому Uб =U_б=U₄; d _б = 0.

В уравнении (1) элементы матриц Yу, Yб выражены в сименсах, Uу, Uб – в кВ, J - в кА, S – в МВА.

Формирование уравнения узловых напряжений (1) начинают с расчета элементов матрицы узловых проводимостей, для чего необходимо:

1.1. Каждой ветви схемы замещения поставить в соответствие некоторое произвольно выбранное направление, изобразить направленный граф электрической сети, пронумеровать его вершины (узлы) и ребра (ветви), указать направление последних, отметить балансирующий узел, составить первую матрицу соединений M (матрицу соединений ветвей и узлов) и транспонированную матрицу M_t.

1.2. Составить диагональную матрицу сопротивлений ветвей схемы Zв и найти обратную ей матрицу Zв^-1 , т.е. матрицу проводимостей ветвей Yв. Ее элемент для i- ой ветви по исходным данным задания рассчитывается так:

,

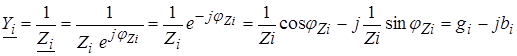или иначе

,

.

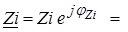
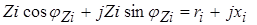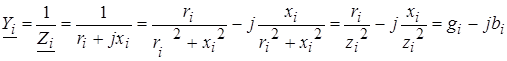1.3. Найти матрицу узловых проводимостей Yу:

.

Матрица узловых проводимостей может быть составлена без выполнения операций умножения указанных матриц непосредственно по схеме замещения сети с учетом проводимостей ее ветвей. При совпадении базисного и балансирующего узлов матрица Yу симметрична относительно главной диагонали, каждый ее диагональный элемент 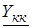равен сумме проводимостей ветвей, связанных с к-м узлом, а каждый недиагональный элемент 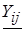равен взятой со знаком минус сумме проводимостей ветвей, соединяющих i-й и j-й узлы схемы.

В результате матрица узловых проводимостей для условий задания получается в виде:

,

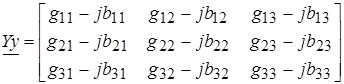или при разделении на матрицы активных и реактивных 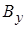составляющих узловых проводимостей:

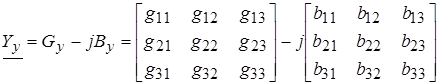. (2)

Элементы матриц и 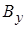в (2) рекомендуется находить по приведенному выше алгоритму непосредственно по схеме замещения сети с учетом рассчитанных в п.1.2 проводимостей ветвей. Вначале рассчитываются все составляющие взаимных проводимостей между узлами к и j:

, ,

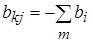где к, j = 1,2,3, к 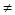j,

m – число параллельных ветвей, соединяющих к-й и j-й узлы,

- активная и реактивная составляющие проводимости ветви i (для условий задания обе положительные).

Составляющие собственной проводимости узла к:

, ;

где l – число ветвей, связанных с к-м узлом.

В (2) для данных условий все диагональные элементы 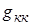и положительны, а недиагональные 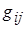, 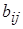- отрицательны. При расчетах элементов матрицы узловых проводимостей не следует делать слишком грубых округлений, сохраняя для значений g и b до четырех значащих цифр.

При решении на компьютере уравнения (1) узловых напряжений, как правило, приводятся к системе действительных уравнений порядка 2n, где n- число независимых узлов.

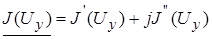Подставим в (1) согласно (2), а также и , где 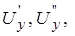- матрицы столбцы действительных и мнимых составляющих напряжений узлов и задающих токов. Приравняв отдельно действительные и мнимые матричные слагаемые, получаем систему уравнений с действительными переменными, которая с целью повышения устойчивости вычислительного процесса записывается в матричном виде так:

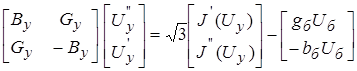. (3)

Система уравнений (3) в развернутом виде для условий задания записывается так:

= ,

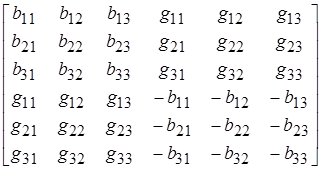
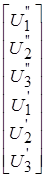или в виде системы алгебраических уравнений, учитывая, что для к-го узла действительная и мнимая составляющие задающего тока определяются выражениями:

Тогда получаем:

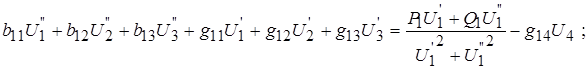
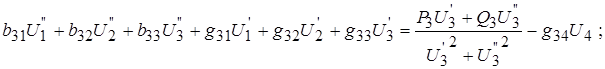
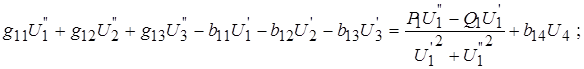(4)

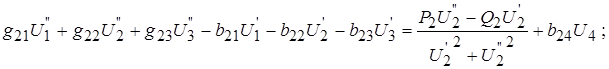
Далее следует подставить в (4) значения активных и реактивных составляющих проводимостей, активных и реактивных мощностей узлов, рассчитываемых по исходным данным задания по формулам , , к = 1,2,3, напряжение базисного узла 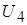. Следует помнить, что в (4) составляющие проводимостей между каждым к-м узлом и базисным , так же, как и все отрицательны, а составляющие собственных проводимостей узлов положительны.

Решение системы нелинейных уравнений узловых напряжений в форме баланса токов с использованием метода Гаусса на каждом шаге итерационного процесса (внешней итерации).

Решение системы уравнений (4) осуществляется в следующем порядке:

2.1. Задаемся начальным приближением неизвестных напряжений узлов на нулевом шаге внешней итерации. Рекомендуется принять 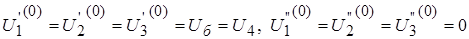. Подставляем эти составляющие напряжений в правые части уравнений (4) и вычисляем числовые значения правых частей. Тогда уравнения узловых напряжений превращаются в систему линейных алгебраических уравнений.

2.2. Решаем систему линеаризованных уравнений методом Гаусса с обратным ходом. В результате выполнения шагов прямого хода исключаем последовательно 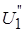из второго и последующих уравнений системы (4) 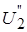из третьего и последующих уравнений и т.д. пока не приведем систему (4) к эквивалентной системе с верхней треугольной матрицей коэффициентов:

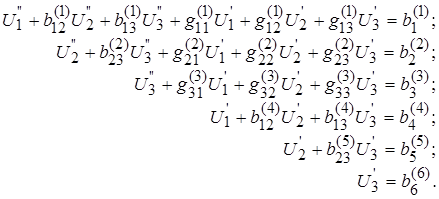(5)

Здесь - значения правых частей линеаризованной системы уравнений (4), а верхние индексы в скобках указывают номер шага прямого хода метода Гаусса.

Из системы (5) последовательно определяем значения неизвестных 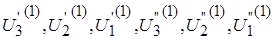(обратный ход). Здесь индекс в скобках указывает номер шага внешней итерации – первое приближение составляющих напряжений узлов.

2.3. Переходим ко второму шагу внешней итерации, т.е. определяем правые части системы (4) при значениях составляющих узловых напряжений, равных их первым приближениям.

2.4. Решая систему линеаризованных уравнений, с той же матрицей , находим второе приближение составляющих напряжений .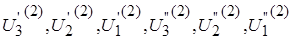

Для выполнения п. п. 2.2 … 2.4 следует воспользоваться программами Excel для схемы 1― КРВр1G и для схемы 2 ― КРВр2G

Можно проверить правильность выполнения аналитических вычислений в п.п.2.2 и 2.4, воспользовавшись программой для ПК решения систем линейных алгебраических уравнений методом Гаусса (С:\STUDENT\MAT_ZAD\LIN_UR), либо программой в системе Mathcad. Такие шаги внешней итерации продолжаются до тех пор, пока процесс не сойдется (с заданной точностью по напряжениям e). В курсовой работе достаточно ограничиться двумя шагами. Значения напряжений в узлах с заданной точностью (e=0,001кВ) следует получить, воспользовавшись программой GAUSS (C:\STUDENT\MAT_ZAD\GAUSS).

Поиск по сайту: