АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение системы нелинейных алгебраических уравнений узловых напряжений в форме баланса токов методом Гаусса-Зейделя

Читайте также:
  1. B. Взаимодействие с бензодиазепиновыми рецепторами, вызывающее активацию ГАМК – ергической системы
  2. CRM системы и их возможности
  3. IV. Поземельные книги и другие системы оглашений (вотчинная и крепостная системы)
  4. VI. ЭТАП Определения лица (группы лиц) принимающих решение.
  5. А если и может, то Конституционный суд отменит это решение в пять минут.
  6. А. промывание полости носа методом перемещения
  7. Автокорреляция в остатках. Критерий Дарбина-Уотсона в оценке качества уравнений, построенных по временным рядам.
  8. Автоматизированное рабочее место (АРМ) таможенного инспектора. Назначение, основные характеристики АРМ. Назначение подсистемы «банк - клиент» в АИСТ-РТ-21.
  9. Автоматизированные информационно-поисковые системы
  10. Автоматизированные системы бронирования, управления перевозками, отправками в аэропортах.
  11. Автоматизированные системы управления воздушным движением.
  12. Автоматические системы пожаротушения.

Для решения системы нелинейных алгебраических уравнений узловых напряжений (4) методом Гаусса-Зейделя приводим ее к виду, удобному для итерационного процесса. Для этого разрешим первое уравнение системы (4) относительно 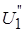, второе – относительно 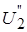и т.д. В результате получаем систему уравнений (6), для к-го шага итераций, эквивалентную (4).

Порядок итерационного расчета

3.1. Задаемся начальным (нулевым) приближением неизвестных .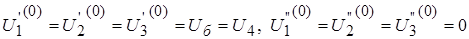

3.2. Значения и , i=1,2,3 подставляем в правую часть первого уравнения системы (6) и определяем первое приближение неизвестного .


 

 

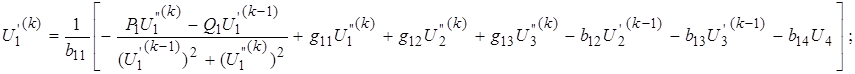(6)

 


При вычислении неизвестного в правую часть второго уравнения системы (6) подставляем значение неизвестного , вычисленное на первом шаге, и нулевые приближения остальных неизвестных и т.д. При вычислении неизвестного в правую часть третьего уравнения системы (6) подставляем значения неизвестных , и нулевые приближения остальных неизвестных и т.д., вплоть до вычисления , когда в правую часть шестого уравнения системы (6) подставляем составляющие напряжений, вычисленные на первом шаге, за исключением , для которого подставляется нулевое приближение .

3.3. Аналогичной подстановкой полученных на первом шаге значений составляющих напряжений в правую часть первого уравнения системы (6) находится следующее приближение и т.д. до достижения требуемой точности.

Таким образом, на каждом к-м шаге итерационного процесса для вычисления i-го неизвестного используются значения неизвестных, вычисленных как на предыдущем к- 1 шаге, так и на данном – к-м.

Значения напряжений в узлах с заданной точностью (e = 0,001 кВ ) следует получить, воспользовавшись программами Excel для схемы 1― КРВр1Z и для схемы 2 ― КРВр2Z. Проверку следует выполнить, воспользовавшись программой ZEIDEL (C:|STUDENT\MAT_ZAD\ZEIDEL).Рассчитанные напряжения следует сопоставить с результатами расчета по программе GAUSS.


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)