 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Чисельні методи розв’язання систем нелінійних рівнянь
Достатньо велика кількість інженерних задач на проміжному етапі вирішення зводиться до вирішення системи нелінійних рівнянь. Це одна з найважчих задач з точки зору реалізації її на ЕОМ. Одним із найбільш простих алгоритмів її рішення є метод Ньютона. Це найбільш розповсюджений метод розв’язання систем нелінійних рівнянь. Його популярність обумовлена тим, що в порівнянні з методом простої ітерації він забезпечує найбільш швидку збіжність. В основі методу Ньютона лежить представлення всіх n рівнянь у вигляді рядів Тейлора.
Розглянемо алгоритм методу Ньютона.
Нехай дана система нелінійних рівнянь виду
 (4.20)
(4.20)
де 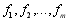 – неперервно-диференційні функції.
– неперервно-диференційні функції.
2. Алгоритм методу базується на розкладі кожної функції системи в околі точки з координатами 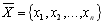 в ряд Тейлора.
в ряд Тейлора.
 члени рядів вищих порядків (
члени рядів вищих порядків (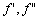 тощо).
тощо).
1. Початкова система буде мати вигляд:
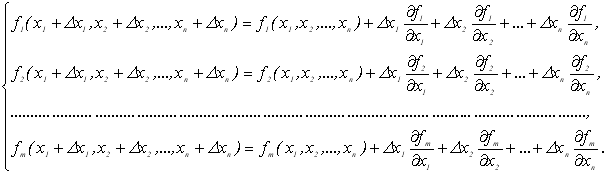 (4.21)
(4.21)
2. Припустимо, що прирости  вибрані таким чином, що точки з координатами
вибрані таким чином, що точки з координатами  є коренями даної системи рівнянь з заданим степенем наближення
є коренями даної системи рівнянь з заданим степенем наближення 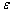 . Тоді ліву частину рівнянь системи (4.21) можна прирівняти до нуля, тобто система рівнянь (4.21) буде мати вигляд:
. Тоді ліву частину рівнянь системи (4.21) можна прирівняти до нуля, тобто система рівнянь (4.21) буде мати вигляд:
 (4.22)
(4.22)
Або в матричній формі система (4.22) буде мати вигляд:
 (4.23)
(4.23)
де  – матриця Якобі.
– матриця Якобі.
3. В результаті таких перетворень система рівнянь може розглядатися як система лінійних алгебраїчних рівнянь відносно  . В такому випадку, якщо врахувати, що заданий вектор х початкових наближень виду:
. В такому випадку, якщо врахувати, що заданий вектор х початкових наближень виду:
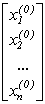 ,
,
можливо розв'язувати систему відносно вектора приросту  , та знайти розв'язок системи, як сума попереднього значення та вектора
, та знайти розв'язок системи, як сума попереднього значення та вектора  :
:
 (4.24)
(4.24)
Дану задачу можна розв'язати з будь-якої точки, вибравши вектор початкових наближень.
4. Процес розв’язання системи нелінійних рівнянь (4.20) з використанням системи лінійних алгебраїчних рівнянь (4.23) відносно  - ітераційний, та буде продовжуватись до тих пір, поки всі координати вектору приростів не стануть менше за абсолютною величиною заданої похибки
- ітераційний, та буде продовжуватись до тих пір, поки всі координати вектору приростів не стануть менше за абсолютною величиною заданої похибки 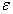 , тобто
, тобто 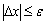 .
.
| Завдання 2 | |||
| Розв'язати систему нелінійних рівнянь з точністю до e=0,01 | |||
| методом простих ітерацій або Ньютона | |||

| |||
| Варіант | |||
| Розв'яжемо систему методом Ньютона-Рафсона | |||
| Для уточненя кореня перетворимо початкові рівняння до виду | |||

| |||
| Відділимо розв'язок системи шляхом табулювання функцій F1, F2 та побудови графіка | |||
| x | F1 | F2 | |
| 0,8 | 2,564901 | 1,28449 | |
| 0,9 | 2,353766 | 1,26231 | |
| 2,09009 | 1,23932 | ||
| 1,1 | 1,768036 | 1,21545 | |
| 1,2 | 1,381766 | 1,1906 | |
| 1,3 | 0,925441 | 1,16467 | |
| 1,4 | 0,393225 | 1,13753 | |
| 1,5 | -0,22072 | 1,10903 | |
| 1,6 | -0,92223 | 1,07898 | |
| 1,7 | -1,71715 | 1,04716 | |
| Наближений розв'язок системи в точці перетину графіків функції при | |||
| x= | 1,3 | y= | |
| Знайдемо | |||

| |||
| Наступні наближення для уточненя коренів рівнян підраховуємо за формулою | |||
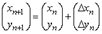
| |||
| Поправки знаходяться з розв'язку системи | |||
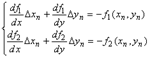
| |||
| Обчислення завершимо при виконанні наступної умови | |||
| max(|xn+1-xn|; |yn+1-yn|)< | e |
| Обчислення проводимо в табличній формі | |||||||||||
| i | xi | yi | df1/dx | df1/dy | df2/dx | df2/dy | -f1 | -f2 | Dx | Dy | max(|xn+1-xn|; |yn+1-yn|) |
| 1,3 | 1,16 | 5,4756 | 1,11 | 1,23 | 4,60195 | -0,26 | 0,0216 | -0,051 | 0,0184 | ||
| 1,249 | 1,18 | 5,05215 | 1,11 | 1,23 | 4,74906 | -0,01 | -0,001 | -0,002 | 0,0003 | 0,051278 |
Поиск по сайту: