 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Упрощенное вычисление ошибки среднего арифметического
При обработке данных по многочисленным вариантам опыта и небольшом количестве повторностей можно применить упрощенный способ вычисления ошибки среднего арифметического по Петерсу с использованием фактора Молденгауэра (константы К) по формуле

где  — сумма отклонений независимо от знака, а К - константа, изменяющаяся в зависимости от количества повторностей, вычисленная по формуле:
— сумма отклонений независимо от знака, а К - константа, изменяющаяся в зависимости от количества повторностей, вычисленная по формуле:

В книге П.Н Константинова «Методика полевых опытов (с элементами теории ошибок)», 1939, дана таблица констант К для ошибок среднего.
(При большем количестве повторностей использование упрощенного способа вычисления ошибки экономит немного времени). Допустим, мы изучали действие различных микроэлементов в разных дозах на урожайность пшеницы. У нас было 40 вариантов опытов. Каждый вариант испытывался в четырех повторностях.
В первом варианте (контроль) был получен следующий урожай (табл. 16).

Для проверки правильности вычисления среднего и отклонений мы сначала суммируем положительные и отрицательные отклонения:
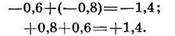
Эти вычисления нужны только для проверки и в дальнейших расчетах не участвуют.
Суммы положительных и отрицательных отклонений равны, значит, вычисления сделаны правильно. (В случае, когда среднее и отклонение вычисляются с округлением, между суммой положительных и отрицательных отклонений может быть небольшая разница, выражающаяся в десятых долях. Этой разнипой можно пренебречь).
Находим сумму отклонений независимо от знака (в нашем примере она равна <3,0) и умножаем ее на константу К для четырех повторностей, равную 0,1809.
3,0х0,1809 = 0.5427
Точность опыта имеет большое значение, так как она определяет степень надежности полученных данных. Точность опыта обозначается Р или m % и вычисляется по формуле
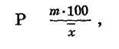
т.е. путем вычисления процентного отношения ошибки к средней величине.
Опыт считают достаточно точным, если Р меньше 3 %, и удовлетворительным при Р, равной 5%. При Р, равной 6-7% и более, к полученным выводам следует отнестись очень осторожно. Опыт следует повторить с соблюдением всех требований методики.
Основная литература: [1-7]
Дополнительная литература: [8-14; 15-17]
Тема 6. Определение достоверности различий между средними .
Конечной целью каждого опыта является установление достоверности различий между изучаемыми вариантами опыта (различие в урожайности сортов, возделывавшихся в производстве, и новыми, выведенными селекционерами; различие в урожайности культур под влиянием внесения удобрений; различие по количественным показателям между разными видами животных и растет и т. д.).
Средние арифметические для выборок всегда несколько колеблются и при указании среднего следует приводить ошибку среднего, показывающую возможные колебания:
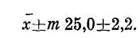
Видно, что среднее колеблется от 22,8 до 27,2. Но поскольку ошибка (m) вычисляется на основе квадратического отклонения (σ), то все возможные значения средней величины лежат в пределах х±3 m или, точнее, х±3,5 m, так же как все варианты ряда, лежат в пределах х-З σ или х+3,5 σ. Отсюда значение 3 m или 3,5 m называется предельной ошибкой среднего арифметического.
Достоверность разности между двумя средними величинами определяют по отношению этой разности к ее ошибке. Ошибка разности равна корню квадратному из суммы квадратов ошибок:
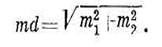
Например, в опыте по изучению влияния фосфорного удобрения на урожай яровой пшеницы в условиях недостатка влаги получены следующие данные (опыт проведен в четырехкратной повторности):
Контроль (без удобрения) — 11,5 ±0,2 ц/га.
При внесении суперфосфата — 13,1 ±0,3 ц/га.
Достоверно ли полученное превышение? Определяем разность между средними:

Вычисляем ошибку разности:

Находим отношение разности к ее ошибке:

В старых руководствах по биометрии указано, что разность достоверна в тех случаях, когда это отношение равно или более трех. Точнее, достоверность разности определяется по критерию Стьюдента t.. t равно отношению разности к ее ошибке.
Рассматриваемый опыт приведен в четырех повторностях. Следовательно, число степеней свободы равно 4+4-2 = 6. При 6 степенях свободы разность при вероятности 0,95 (на уровне 5%) достоверна при t, равном 2,45, при вероятности 0,99 (на уровне 1%) при t, равном 3,71. Следовательно, разность между урожаем контрольного и опытного вариантов достоверна при уровне вероятности, несколько превышающем 0,99.
Основная литература: [1-7]
Дополнительная литература: [8-14; 15-17]
Тема 7. Учение о корреляциях.
Слово корреляция происходит от латинского correlation, что означает связь, соотношение, сопряженность. В практике биологических исследований часто возникает необходимость изучить связи между признаками одного организма или зависимость между признаками организма и условиям внешней среды.
В курсе высшей математики излагаются основные положения функциональной зависимости между двумя переменными, при которой каждому значению одной переменной - аргументу соответствует тоже одно вполне определенное значение другой переменной — функции.
В качестве примера функциональной зависимости можно привести площадь треугольника, которая всегда определяется его высотой и основанием, площадь круга, определяющуюся его радиусом, и т.д.
При изучении живых объектов - растений, животных, микроорганизмов — связь между признаками проявляется в виде так называемой корреляционной связи или корреляции, при которой каждому значению одного признака соответствует не одно, а несколько значений другого признак; т.е. его распределение.
Например, хорошо известна связь между ростом человека и его весом, но при одинаковом росте (например, в 160 см) вес тела может колебаться в известных пределах и составлять, допустим, 55, 60, 65 кг. Задача исследования корреляционной связи заключается в том, чтобы определить xapaктер и измерить тесноту связи между отдельными признаками или развитием признаков и условиями среды.
При изучении корреляции решающее значение имеет всесторонний качественный анализ материала. Например изучая зависимость между содержанием белка в зерне и условиями возделывания культуры, необходимо сопоставить эти показатели в образцах одного сорта, выращенного при различных, но вполне определенных в каждом отдельном случае условиях. Так, если мы хотим установить зависимость содержания белка в зерне озимой пшеницы Безостая 1 от применения азотных удобрений, необходимо, чтобы остальные условия (тип почвы, предшественники, приемы обработки почвы, сроки посева и т.д.) были одинаковыми, а изменялась только доза внесения азотных удобрений.
Прежде чем приступить к вычислению корреляционной зависимости, необходимо проанализировать возможность связи между изучаемыми явлениями, иначе можно получить совершенно ложные результаты. Так, в работе Устинова была установлена корреляция между урожайностью и числом пожаров.
Известно, что засуха всегда снижает урожай, что опасность пожаров увеличивается в сухие годы. Таким образом, два совершенно независимых явления (пожары и урожай) определяются третьей величиной - количеством осадков, но сопоставлять эти два явления нет никаких оснований.
Зависимость урожая от количества осадков может быть различной в разных географических пунктах. В районах недостаточного увлажнения, при отсутствии орошения, уменьшение количества осадков всегда снижает урожай, хотя степень этого снижения может быть различной в зависимости от уровня агротехники; в районах избыточного увлажнения, наоборот, увеличение количества атмосферных осадков может быть неблагоприятным для урожая, особенно при недостатке тепла. Следовательно, установление корреляции между этими величинами представляет интерес в определенных географических условиях.
Для разработки рациональной системы орошения большое значение имеет установление связи между обеспеченностью растений влагой в определенные периоды развития и урожайностью и т. д.
Корреляция может быть прямой или положительной, если с возрастанием одного показателя увеличивается второй или, наоборот, с уменьшением одного показателя уменьшается второй.
Такая корреляция выражается словами «чем больше, тем больше» или «чем меньше, тем меньше». Например, чем больше вес клубней картофеля в одном гнезде, тем выше урожай; чем меньше длина туловища животного определенного вида, тем меньше его вес.
Корреляция является обратной или отрицательной, если с увеличением одного показателя уменьшается второй или с уменьшением первого показателя увеличивается второй. Такая зависимость выражается словами: «чем меньше, тем больше» или «чем больше, тем меньше». Например, чем больше растений кукурузы в гнезде, тем меньше початков на растении.
Как прямая, так и обратная корреляция может быть линейной, если с увеличением одного показателя планомерно увеличивается или уменьшается второй показатель, или криволинейной, если с увеличением одного показателя до известных пределов второй показатель также повышается, а затем начинает снижаться. Например, при увеличении нормы высева до определенного для конкретных условий уровня урожай повышается, но дальнейшее увеличение нормы высева вызывает излишнее загущение посева, и урожай снижается. Степень сопряженности выражается в виде отвлеченного числа, которое при корреляции называется коэффициентом корреляции, при криволинейном зависимости — корреляционным отношением.
Основная литература: [1-7]
Дополнительная литература: [8-14; 15-17]
Тема 8. Вычисление коэффициента корреляции.
Многие авторы рекомендуют располагать варианты горизонтального ряда в восходящем, и вертикального - в нисходящем порядке. В этом случае первый чертеж будет изображать отрицательную корреляцию, второй чертеж — положительную. О том, какой порядок расположения вариант принят данным автором, говорят цифры, стоящие сбоку и снизу корреляционной решетки в работах, где используется графическое изображение корреляционной зависимости.
Однако такой способ слишком громоздок и неприменим в случаях, когда надо показать корреляцию по ряду признаков. Кроме того, он дает лишь ориентировочное представление о тесноте связи между изучаемыми признаками, поэтому прибегают к вычислению коэффициента корреляции. Коэффициент корреляции обозначается г. Он является отвлеченным числом и имеет значение от 1 (полная положительная корреляция) до -1 (полная отрицательная корреляция) с переходом через 0 (отсутствие корреляции). Так же, как и для других биометрических показателей, вычисляется ошибка коэффициента корреляции — mr или -Sr.
Основная литература: [1-7]
Дополнительная литература: [8-14; 15-17]
Планы семинарских занятий.
Тема 1. Введение. Изменчивость и пути ее изучения .
Задание№1.
Опишите историю развития биометрии за последние 30 лет.
Задание № 2.
Опишите основные этапы развития применения математических методов в вбиологии.
Задание № 3.
Сравните биометрию и математику применяемую в биологии..
Задание № 4.
Раскройте смысл утверждения, что статистика является одним из самых могучих орудий социального познания.
Задание № 5.
Ответьте на следующие вопросы:
1. Когда и кем были применены методы математической статистически для изучения биологических явлений.?
2. Что такое изменчивость и назовите виды изменчивости?
Тема 2. Разбивка вариант на классы. Составление гистограмм, замена гистограмм кривыми. Двухвершинные и многовершинные кривые, протуберанцы ошибок.
Задание№1.
Качественная и количественная изменчивость. Статистическая совокупность. Общие и частные статистические совокупности. Правила соблюдаемые при разбивке вариант на классы. Построение гистограмм.
.Двухвершинные и одновершинные кривые. Протуберанцы ошибок.
Задание№2. Найдите амплитуду изменчивости, составьте вариационный ряд, найдите частоту вариант.
Измерения высоты стеблей пшеницы сорта №41339 (см) дало следующие результаты:
65 75 62 58 69 64 66 65 65 62 69 73 71 69 73 71 61 79 64 66 63 60 73 76 65 64 65 66 70 54 78 79 71 60 59 66 74 50 71 73 66 79 69 77 64 64 62 72 83 74 69 73 65 61 64 58 68 56 66 64 n=60
Задание №3.
Изобразите вариационный ряд графически.
Тема Вычисление арифметического среднего, основного (квадратического) отклонения, коэффициента вариации .
Задание№1.
1. Найдите основное квадратическое отклонение (сигма) и ошибку арифметического среднего.
2. Найдите сумму положительных и отрицательных отклонений (по сортам).
3. Упрощенное вычисление ошибки среднего арифметического.
Задание №2.
1. Изобразите вариационный ряд графически.
2. Вычислите арифметическую среднюю, ошибку среднего арифметического, сигму, коэффициент вариации.
1 задача
21 28 25 32 38 42 31 32 26 22 24 39 35 40 32 34 21 24 31 30 35 37 27 28 32 31 28 30 33 26 25 36 37 39 29 27 28 30 21 28 36 26 33 28 31 38 35 n=50
2 задача
38 55 47 60 54 59 49 62 66 46 56 55 51 52 52 45 47 52 45 66 37 49 46 49 46 51 43 51 41 52 46 52 39 69 36 42 49 42 47 41 50 47 45 47 54 43 45 46 47 48 n=50
38 55 47 60 54 59 49 62 66 46 56 55 51 52 52 45 47 52 45 66 37 49 46 49 46 51 43 51 41 52 46 52 39 69 36 42 49 42 47 41 50 47 45 47 54 43 45 46 47 48 n=50
Тема 4. Показатели разнообразия признаков .
Задание№1.
1. Показатели разнообразия признаков (лимит, амплитуда варьирования, сигма және коэффициент вариации)
2. Значимость лимита и амплитуды варьирования в сельском хозяйстве.
Задание №2.
1. Нарисуйте вариационную кривую, гистограмму.
2. Вычислите арифметическую среднюю, ошибку среднего арифметического, сигму, коэффициент вариации.
1 задача
91 95 96 101 100 102 108 109 106 103 105 104 90 94 93 92 97 98 99 91 95 96 99 98 102 104 105 109 101 100 102 108 93 92 97 94 106 107 99 96 95 104 100 101 102 109 108 107 105 102 106 104 105 105 105 108 109 107 104 102 102 101 106 106 110 110 117 118 113 115 111 114 112 116 115 114 114 112 111 110 111 110 116 113 113 117 112 105 n =100
2 задача
21 28 25 32 38 42 31 32 26 22 24 39 35 40 32 34 21 24 31 30 35 37 27 28 32 31 28 30 33 26 25 36 37 39 29 27 28 30 21 28 36 26 33 28 31 38 35 n=50
Тема 5. Среднее квадратическое отклонение (сигма). Ошибка среднего арифметического .
Задание№1.
1. Средняя геометрическая.
2. Средняя квадратическая.
3. Средняя гармоническая.
4. Взвешенное среднее.
Задание №2.
1. Нарисуйте вариационную кривую, гистограмму.
2. Вычислите арифметическую среднюю, ошибку среднего арифметического, сигму, коэффициент вариации.
80 75 75 72 82 89 86 86 87 86 71 77 81 70 80 80 80 88 87 88 90 89 78 78 77 79 79 80 81 72 74 73 73 74 73 75 76 76 77 81 80 82 82 8\3 85 84 78 79 85 84 85 84 77 71 74 80 79 83 81 82 81 81 81 82 n=65
Тема 6. Определение достоверности различий между средними .
Задание№1.
1. Практическое значение вычисления ошибки среднего арифметического.
2. Достоверности различий между средними.
Задание№2.
Определите достоверность различий между средними двумя способами – классическим и по критерию Стьюдента (t):



Тема 7. Учение о корреляциях.
Задание № 1
1. Корреляционная связь.
2. Прямая и обратная корреляция.
3.Коэффициент корреляции и графическое изображение корреляции.
Задание №2
Определите коэффициент корреляции (г) и ошибку коэффициента корреляции (mr) между длиной лучевой кости человека (X) и длиной стопы (У):

Тема 8. Вычисление коэффициента корреляции.
1. Вычисление коэффициента корреляции.
2. Градации коэффициента корреляции.
Определите коэффициент корреляции (г) и ошибку коэффициента корреляции (mr) между кустистостью пшеницы сорта Қызылбас (X) и числа зерен (У):

8.Планы лабораторных занятий Не запланировано
Поиск по сайту: