Лекционный комплекс (тезисы лекций)

Различают прерывное варьирование и непрерывное. Прерыв­ное варьирование изучается путем подсчетов и называется так потому, что разница между отдельными особями всегда выражается в целых числах и не может быть меньше единицы. (В колосе пшеницы может быть 10, 15, 46 и т.д. зерен, но не может быть 10,5 зерна).

Непрерывное варьирование определяется путем измерения, взвешивания, химических анализов. В этих случаях изучаемые количественные признаки выражаются как целы­ми, так и дробными числами. Чем больше точность измере­ния, тем меньше возможная разница между близкими объек­тами. (Например, расстояние между двумя точками мы можем измерять километрами, метрами, сантиметрами, миллиметрами, и чем точнее будет измерение, тем меньше разница между соседними измерениями). Переход от мини­мального к максимальному значению постепенный.

Отбор выборок без преднамеренного подбора, случайно, называется рендомизированным отбором. К этой же категории отбора выборок относится взятие для анализа каждого 10-го, 20-го и т. д. экземпляра, например, при изу­чении изменчивости рыб или анализе початков кукурузы, а также в ряде других случаев.

Рассмотрим конкретный пример. Нам надо определить число колосков в колосьях пшеницы данного сорта. Размер выборки - 50 колосьев. Отобрав рендомизированно необхо­димое количество (50) колосьев, мы приступаем к подсчетам (табл. 1). Сначала пишем: «Число колосков и колосе (Казах­станской 126 или другого изучаемого сорта)».

Поскольку мы растения брали без выбора, то в таблице 1 цифры расположены без каких-либо закономерностей и из нее нельзя сделать никаких выводов.

Количественное выражение признака называется вари­антой или (у некоторых авторов) датой и изображается буквами V или х. Варианты, расположенные в восходящем или нисходящем порядке, образуют вариацион­ный ряд. Чтобы составить вариационный ряд, найдем и отме­тим максимальную и минимальную варианты. В нашем примере минимальная варианта - 12, максимальная - 20. Разность между минимальной и максимальной вариантами называется размахом варьирования или амплитудой измен­чивости.

Для составления вариационного ряда расположим вари­анты в восходящем порядке и определим, сколько раз каж­дая варианта встречается в нашей выборке.

Число, показывающее, сколько раз встречается в данной выборке каждая варианта, называется частотой и изобра­жается буквами f или р. Для определения частот произве­дем разноску: зачеркиваем первую цифру таблицы 2 и про­тив варианты 18 ставим точку, затем за­черкиваем вторую цифру – 13, ставим точку против варианты 13, зачеркиваем третью цифру и ставим точку против ва­рианты 20 и т. д. Числа 1, 2, 3, 4 изобра­жаются точками; 5 и 6 - диагоналями, 7, 8, 9, 10 - сторонами квадрата. Закон­чив разноску наших данных, заменим точки и черточки цифрами - узнаем частоты. Сумма частот должна быть рав­на количеству взятых для исследования объектов. В нашем примере 2+6+8+12+8...+1 = 50, следовательно, раз­носка произведена правильно. Правиль­ность разноски обязательно надо проверять, иначе допущен­ная и незамеченная своевременно ошибка при разноске сде­лает неверной всю дальнейшую работу. Сумма в вариацион­ной статистике изображается заглавной буквой «сигма» гре­ческого алфавита - Σ, количество объектов исследования — латинской буквой n. Запишем первую формулу:

Изобразим наш вариационный ряд графически (рис.1); на горизонтальной оси отложим варианты, на вертикаль­ной - частоты. Рабочие графики удобно делать на клетчатой или мил­лиметровой бумаге.

Таблица 2

Графическое изображение вариационного ряда называет­ся вариационной кривой, наиболее часто встречающаяся в ва­риационном ряду вари­анта - модой. В нашем примере мода равна 15. Варианта, расположен­ная в середине вариаци­онного ряда, называется медианой. Мода изобра­жается Мо, медиана - Me. В биологических исследованиях мода имеет большое значение.

Рис. 1. Число колосков в колосс пшеницы Казахстанская 126.

Разбивка вариант на классы. составление гистограмм. замена гистограмм кривыми. Двухвершинные и многовершинные кривые, протуберанцы ошибок.

Исследуя непрерывную изменчивость, а также анализи­руя данные, полученные при изучении npеpывной изменчи­вости при большом размахе варьирования, необходимо раз­бивать варианты на классы. Например, число икринок у рыб одного вида и возраста нередко изменяется более чем на 500. Совершенно ясно, что выписывать столбиком все вари­анты невозможно. При непрерывной изменчивости варианты чаще всего представлены смешанными числами: высота растений - 1,25; 2,15; 3,45 м и т. д. Содержание белка в зерне пшени­цы - 15,2; 16,01; 16,5% и т. д. Между двумя целыми чис­лами может располагаться 100 вариант, различающихся на 0,01 м или 0,01%.

В этих случаях варианты разбиваются на классы. При этом следует соблюдать следующие правила:

1. Границы классов должны быть такими, чтобы каждая варианта могла быть отнесена только к одному классу: 5-9, 10-14, 15-19 т.д., но не 5-10, 10-15,15-20 и т.д.

2. Размеры всех классов должны быть равными.

3. Первый и последний классы могут быть неполными. Например, при размере класса 10 и амплитуде изменчивости 76, размер последнего класса 70-79, хотя варианты 77-79 в нашем примере отсутствуют.

4. Количество классов должно быть не более 10-15 и не менее 6-7.

5. Для определения размера классов находят минималь­ную и максимальную варианты, определяют амплитуду изменчивости и делят ее на установленное количество клас­сов, округляя полученное число до целого. Например: изме­рения высоты стеблей кукурузы 25/VIII 1972 г. дало резуль­таты, приведенные в таблице 3.

Таблица 3

Амплитуда варьирования 100-179 = 79 см. Если при­мем размер класса за 10, то 79:10 = 7,9=8 классов. Наме­тим границы классов и составим таблицу 4.

При разноске мы зачеркиваем в нашей таблице очеред­ную цифру и ставим точку или черточку против соответст­вующего класса. Так, в класс 100-109 мы отнесем вари­анты 100, 102, 103, 105, 106, 108. Мы получили вариацион­ный ряд. Мода его - класс 130-139.

Графическое изображение вариационного ряда, разбито­го на классы, называется гистрограммой. При составлении гистрограммы на горизонтальной оси наносятся размеры классов, на вертикальной — частоты. Гистрограмму можно превратить в вариационную кривую. Для этого надо соеди­нить прямыми линиями середины классов. Изобразим при помощи гистрограммы полученные нами данные по высоте растений кукурузы (рис.2).

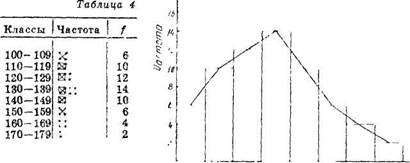
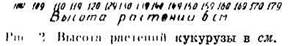
При анализе количественных данных исследователь обычно получает много чисел. Построение гистограмм и ва­риационных кривых помогает осмыслить эти числа, наме­тить определенные закономерности. Графики чисто поме­щают в печатных изданиях и в отчетах научно-исследова­тельской работе. Для удобства сравнения на одном чертеже помещают несколько кривых. На рабочих чертежах удобно эти кривые чертить цветной тушью или карандашами. Для печати кривые обычно чертят черной тушью, но разными шрифтами. Каждый чертеж сопровождается экспликацией, показывающей, как изображен тот или другой вариант опы­та. Например, мы провели измерение высоты пяти гибридов кукурузы. Экспликация будет выглядеть следующим обра­зом:

Гибрид ВИР156 (контроль) Юбилейный, Днепровский 56, Краснодарский 4, Южный 3

На одном чертеже неудобно располагать больше 5-6 ва­риантов опыта, поэтому если сравнивается большее коли­чество вариантов опыта, то составляется несколько графи­ков, причем вариант, служащий контролем, помещается на каждом чертеже. Чтобы на одном чертеже можно было по­местить несколько кривых, при разбивке вариант на классы надо границы классов устанавливать не по минимальной варианте каждого варианта опыта, а брать границы классов, общие для всех вариантов. Например, если минимальная высота растений в одном варианте опыта 100, в другом - 113, в третьем - 98 см, а размер класса принят за 10 см, то границы классов должны быть 90-99, 100-109, 110-119 и т.д. То, что первые классы могут отсутствовать или быть неполными, не имеет значения.

Для большинства признаков сельскохозяйственных и биологических объектов характерно нормальное распреде­ление. Его отличительной чертой является то, что, чем боль­ше отклоняется значение отдельной варианты от средней, тем реже она наблюдается. Например, большинство людей имеет средний рост. Великаны (более 200 см) и карлики (менее 100 см) встречаются крайне редко.

Наиболее часто отклоняются от нормального скошенное (асимметрия), крутовершинное (эксцесс), двух- и многовер­шинное распределения (рис. 3).

Рис. 3. Типы распределе­ний. Пунктиром показано нормальное распределение.

В практической работе иногда наблю­дается резкое снижение или возрастание частоты отдельных вариант. Такие выступы на кривых называются протуберанцами ошибок. Причины их возникновения:

1. Недостаточное количество объектов исследования.

2. Слишком мелкие градации изучаемых признаков.

3. Допущенные ошибки в измерениях или подсчетах.

Например, изучая количество зерен в колосьях пшеницы определенного сорта, мы получили данные, представленные в таблице 5. Если мы объединим количество зерен в классы по два, то кривая примет нормальный вид (рис. 5). Это естест­венно, так как разница в одно зерно может быть слу­чайной.

Основная литература: [1-7]

Дополнительная литература: [8-14; 15-17]

Одна из основных задач статистической обработки мате­риала - найти показатели, характеризующие особенности эмпирических совокупностей, дающие возможность сравни­вать их друг с другом.

Статистические совокупности с достаточной полнотой характеризуют два показателя:

1. Средняя величина признака;

2. Степень варьирования или рассеяния. Рассмотрим понятие «средняя величина признака». В статистике используются средняя арифметическая, средняя взвешенная, средняя гармоническая, средняя геометриче­ская. Наибольшее значение в биологических и сельскохозяй­ственных исследованиях имеет средняя арифметическая.

Средней арифметической называется такая величина, сумма отрицательных и положительных отклонений от кото­рой равна нулю. Например, количество плодов на растениях составляет 4; 5; 9. Среднее количество плодов - 6; 4 откло­няется от 6 на минус 2; 5 - на минус 1; 9 - на плюс 3:

Чтобы найти арифметическое среднее, надо сложить все варианты и разделить их на число наблюдений.

Средняя арифметическая в вариационной статистике обозначается как М или х (читается как икс покрытое). Фор­мула определения среднего арифметического:

При небольшом количестве наблюдений или при исполь­зовании электронных счетных машин вычисление среднего арифметического производится таким образом.

При обработке сложных вариационных рядов при боль­шом количестве вариант такой способ вычисления слишком трудоемок. Применяется способ вычисления среднего «по способу моментов», или «от произвольного начала». Рас­смотрим этот способ вычисления на примере простого вариа­ционного ряда (табл. 6). (Вариационный ряд, в котором каж­дая варианта встречается один раз называется простым, несколько раз - сложным).

Отклонения от произвольно взятого среднего обозна­чаются а или х-х. В качестве произвольно и взятого среднего (или условного среднего) берем любую варианту, лежащую в средине или близко к средине вариационного ряда. Отгра­ничиваем ее прямыми линиями. Мы взяли в нашем примере в качестве произвольного среднего варианту 13.

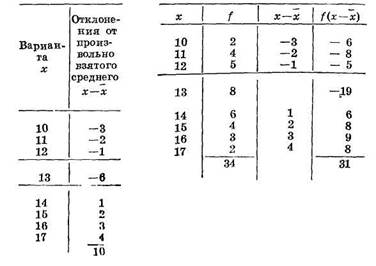
Таблица 6 Таблица 7

Вычислим отклонения от произвольной средней каждой варианты. По­скольку наш ряд построен в восходящем порядке, варианты, лежащие выше произвольного среднего, имеют знак -, ни­же его +

Найдем алгебраическую сумму отклонений:

Мы знаем, что сумма отрицательных и положительных отклонений от среднего равна 0. Разделив полученную нами сумму отклонений на число наблюдений (8), получаем поправку.

I

Формула поправки , а истинное среднее равно произвольно взятому среднему Мо + поправка.

Нельзя забывать, что речь идет об алгебраической сум­ме: если мы получили поправку с отрицательным знаком, то

В нашем примере М или Проверим наше вычисление:

Мы получили одинаковые результаты, что и при вычисле­нии с помощью произвольно взятой средней.

Если в качестве произвольного среднего мы возьмем варианту 14, то сумма отрицательных отклонений будет равна - 10; сумма положительных +6, поправка

b = -10+6/8= - 0,5. Среднее = 14+(-0,5) = 13,5.

Для проверки правильности вычисления среднего реко­мендуется повторить вычисление, взяв за произвольное сред­нее другую варианту.

В сложных вариационных рядах, где варианты встре­чаются по нескольку раз, также берут одну из вариант, лежащих в средине ряда, за произвольную среднюю, вычис­ляют отклонение от среднего (х—х или а), умножают откло­нения на соответствующие частоты, находят суммы положи­тельных и отрицательных отклонений (а х f), делят на количество наблюдений и найденную таким образом поправку добавляют или вычитают произвольно взятого среднего (в зависимости от знака). Рассмотрим пример (табл. 7).

Поправка b= -19+31/34=0,35, п=34. Вычисления производятся с точностью до 0,01. Средняя равна 13+0,35 = 13,35.

При вычислении среднего в рядах, разбитых на классы, во избежание получения слишком больших чисел при рас­четах, отклонения от произвольно взятого среднего каждого класса принимают за единицу, а затем полученную поправ­ку умножают на размер классового промежутка, обозначае­мого К или l, и добавляют или вычитают (в зависимости от знака) к центральному значению класса, взятого в качестве произвольного среднего. Центральное значение класса обоз­начается W, X или х. В качестве примера вычислим среднее по данным таблицы 8.

Сумма произведений частот на отклонение с отрицатель­ным знаком равна - 20, с положительным знаком 34. Алге­браическая сумма составляет 14. Найдем b, для этого 14 разделим на получим 0,34. W — центральное значение класса, принятого за среднее, равно 37. Отсюда М= 37 +0,34 х5= 38,70.

Таблица 8

Формула вычислении среднего вариационного ряда, раз­битого на классы:

M=W+bl

При исчислении следует следить за правильностью зна­ков gлюс или минус у b.

Основная литература: [1-7]

Дополнительная литература: [8-14; 15-17]

Квадратическое (основное) отклонение (сигма) используется для вычисления очень важного статистического показателя — ошибки среднего арифметического. Точное сред­нее арифметическое может быть определено, если мы иссле­дуем всю генеральную совокупность. Практически же мы имеем дело с более или менее большими по объему выборка­ми. В таких случаях среднее всегда бывает не вполне точ­ным.

Возьмем 100 растений, измерим их высоту, вычислим среднюю арифметическую. Допустим, что средний рост рас­тений данной выборки 50,5 см. Разобьем эти растения на группы по 20 экз. в каждой. Вновь проведем измерения и вычислим средние. Эти новые средние точно не совпадут с уже установленным средним 50,5, а будут в каждом отдель­ном случае отклоняться от него в ту или другую сторону: 49,8; 50,9; 50,1; 51,3; 50,4 в зависимости от того, попадут ли во взятую для измерения группу более высокие или более низкие растения. Поэтому, называя среднее арифметичес­кое, необходимо указать и возможные колебания этой сред­ней величины. Это достигается путем вычисления ошибки среднего арифметического, которая обозначается m или Sx и определяется по формуле

Приводя среднее арифметическое, указывают и его ошибку:

Это показывает, что среднее в исследованной выборке колеблется от 140 до 150.

Ошибка средней арифметической зависит от двух вели­чин: от степени разнообразия признака в генеральной сово­купности и от размера выборки: чем больше выборка, тем меньше ошибка. Поэтому при вычислении ошибки квадратическое отклонение делится на корень квадратный из числа наблюдений.

Часть никогда не может полностью характеризовать це­лое, поэтому характеристика генеральной совокупности на основе выборочных данных всегда будет иметь некоторую большую или меньшую ошибку. Такие ошибки являются ошибками обобщения, связанными с перенесением результатов, полученных при изучении выборки, на всю генераль­ную совокупность, и называются ошибками репрезентатив­ности. (Репрезентативность происходит от французского сло­ва representative - представительный).

Помимо ошибок репрезентативности при исследовании могут встретиться ошибки самого разнообразного характера. К ним относятся:

1. Методические ошибки (нарушение правильной мето­дики проведения фиксации материала для цитологических и биохимических исследований, невыравненность условий в опытных вариантах и контроле).

2. Ошибки точности (использование непроверенных изме­рительных приборов, расчеты с недостаточной точностью и т. д.).

3. Случайные ошибки (ошибки, просчеты, путаница в материале и т. д.).

4. Ошибки, связанные с неправильным отбором проб для изучения.

Все эти причины повлекут за собой очень сильное увели­чение ошибки среднего. (Иногда у начинающих работников ошибка бывает почти равна среднему. Ясно, что такие дан­ные должны выбраковываться).

Поиск по сайту: