АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Средняя арифметическая

Читайте также:
  1. Арифметическая середина и ее свойства.
  2. Взвешенная средняя арифметическая
  3. Вопрос 29. Средняя геометрическая и её определяющее свойство
  4. ГОРОДА НОВОСИБИРСКА «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 45» (МБОУ СОШ № 45)
  5. Деление дохода на потребление (C) и сбережения (S). Средняя и предельная склонность к потреблению (АРС, МРС) и сбережения (APS, MPS).
  6. Доход семьи составил 500 ден.ед., а потребительские расходы – 450 ден.ед. Чему равна в этом случае средняя склонность к сбережению?
  7. Иран и Средняя Азия в 1 веке.
  8. По этой формуле рассчитывается средняя квадратическая ошибка прогноза у0 с волной
  9. Потребление и сбережение, факторы их определяющие. Предельная склонность к потреблению и сбережению. Средняя склонность к потреблению и сбережению.
  10. Потребление: факторы и функция. Средняя и предельная склонность к потреблению.
  11. Производственное и непроизводственное потребление. Средняя и предельная склонности к потреблению. Функция и график потребления.
  12. Психологическая склонность к потреблению и сбережению. Средняя склонность к потреблению и сбережению. Предельная склонность к потреблению и сбережению, их взаимосвязь.

Средняя арифметическая представляет собой как бы точку равновесия вариационного ряда, отклонения от которой в сторону увеличения или уменьшения признака взаимно уравновешиваются. Средняя арифметическая показывает, какую величину признака имели бы особи данной группы, если бы эта величина была у всех одинаковой.

Простейший метод вычисления средней арифметической величины для небольшой выборки (n<30) – это простое суммирование, т.е. нахождение суммы вариант выборки и деление ее на объем выборки. Среднюю арифметическую обозначают Хср или М.

 
 

где X – величина варьирующего признака;

n – объем выборки;

S – знак суммирования.


Для больших выборок среднюю арифметическую удобнее вычислить косвенным методом по формуле:

 
 

где А – условное среднее значение нулевого класса;

р – частоты;

а – условное отклонение;

n – объем выборки;

i – величина классового промежутка.

Задание. Пользуясь вариационным рядом, представленным в таблице 1, составить таблицу 2 для вычисления средней арифметической косвенным методом.

Распределение вариант по весу Таблица 1

Границы классов (Wн – Wк) Частоты (р)
42 – 45  
46 – 48  
49– 51  
52 – 54  
55 – 57  
58 – 60  
61 – 63  
64 – 67  
  Sр = n = 50

 

Таблица 2

Рабочая таблица для вычисления средней арифметической

методом условных отклонений

№ класса Границы классов (Wн – Wк) Частоты (р) Условные отклонения (а) Произведение условных отклонений на частоты (ра)
  42 – 45   –3 –3
  46 – 48   –2 –10
  49 – 51   –1 –12
  52 – 54      
  55 – 57      
  58 – 60      
  61 – 63      
  64 – 67      
  Sр = n = 50     Sра = 9

 

Для вычисления средней арифметической необходимо:

1 Найти в построенном вариационном ряду условный средний класс. В качестве условного среднего класса рекомендуется брать класс, который занимает центральное место в данном вариационном ряду и имеет наибольшее по сравнению с другими классами значение частот (р). В нашем примере условным средним классом будет четвертый класс с наибольшей встречаемостью вариант (р = 14) и варьированием веса в пределах 52 – 54 кг.

2 Выделить условный средний класс линиями и принять за нулевой.

3 Вычислить условное среднее значение нулевого класса. Его обозначают буквой А.

В нашем примере

 

4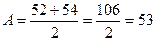
Определить условное отклонение (а) каждого класса от нулевого путем вычитания порядкового номера нулевого класса от порядкового номера других классов. Вверх от класса, принятого за условный нулевой, получим натуральный ряд отрицательных чисел (–1, –2, –3 и т.д.), вниз – натуральный ряд положительных числе (+1, +2, +3 и т.д. в зависимости от класса).

5 Найти произведение частоты на условное отклонение для каждого класса (ра) и заполнить графу.

6 Найти сумму частот (Sр = n = 50).

7 Вычислить сумму произведений частот на условное отклонение. Она равна:

Sра = –25+34 =9.

8 Вычислить среднее арифметическое по формуле:


где А – условное среднее значение нулевого класса;

i – величина классового промежутка.


Таким образом, средний вес равен 53,5 кг.

 

 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)