Подготовка к лабораторной работе

1. Повторить программирование в системе Mathcad.

2. Изучить соответствующие разделы в литературе [1-3].

Краткая теория

Описанный ниже код устраняет некоторые недостатки, присущие кодам NRZ и RZ. При передаче нуля он передаёт потенциал, который был установлен на предыдущем такте (то есть не меняет его), а при передаче единицы потенциал меняется на противоположный, таким образом достигается самосинхронизация при передаче длинных последовательностей единиц (рисунок 5.1). Этот код называется потенциальным кодом с инверсией на единице (NRZI - Non Return to Zero with ones Inverted). Этот метод, как и два предыдущих, удобен в тех случаях, когда наличие третьего (и более) уровня сигнала весьма нежелательно, например, в оптических кабелях, где устойчиво распознаются только два состояния сигнала – свет и темнота.

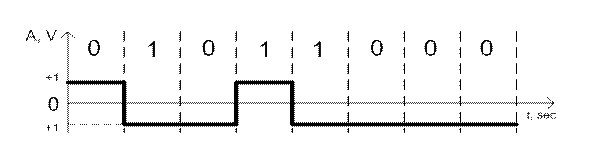
Рисунок 5.1 – Код NRZI

К достоинствам данного метода можно также отнести узкий спектр и отсутствие поляризации.

Недостатком является плохая синхронизация при передаче длинных последовательностей нулей.

Порядок выполнения:

1. Открыть рабочий лист Mathcad, созданный в предыдущих лабораторных работах.

2. Разработать Mathcad-функцию NRZI-кодер аналогично лабораторным работам 3, 4.

3. Разработать Mathcad-функцию NRZI -декодер.

4. Закодировать с помощью функции из п.2 поочередно входные последовательности данных, заданные в лабораторной работе №1:

· последовательность нулей;

· последовательность единиц;

· последовательность чередующихся нулей и единиц;

· текстовая строка.

5. Передать поочередно полученные кодовые последовательности с помощью модели канала, разработанной в лабораторной работе №2.

6. Декодировать поочередно полученные приемником сигналы с помощью функции из п.3.

7. С помощью Mathcad-функций berCalc() и serCalc() из лабораторной работы №1 вычислить интенсивность битовой (символьной) ошибки для каждой последовательности.

8. Свести результаты работы в таблицу (приложение 1).

9. Оформить отчет в виде Mathcad-файла.

10. Сдать и защитить работу.

Содержание отчёта по лабораторной работе:

1. Номер название и цель лабораторной работы.

2. Задание к лабораторной работе.

3. Разработанные в лабораторной работе функции.

4. Результаты выполнения с пояснениями.

5. Выводы по лабораторной работе.

Контрольные вопросы:

1. Опишите принцип NRZI-кодирования.

2. В чем заключается преимущество кода NRZI перед кодами NRZ и RZ, а в чем он им уступает?

3. Какие требования предъявляются к методам цифрового кодирования?

4. В чем разница между потенциальными и импульсными кодами?

5. Перечислите недостатки NRZI-кода.

6. Чем определяется ширина спектра закодированного сигнала?

Лабораторная работа №6

Биполярное кодирование с альтернативной инверсией AMI

Цель работы: Изучение методов цифрового кодирования сигналов на примере кода AMI. Исследование процесса передачи данных на физическом уровне.

Подготовка к лабораторной работе:

1. Повторить программирование в системе Mathcad.

2. Изучить соответствующие разделы в литературе [1-3].

Краткая теория:

Еще одной модификацией метода NRZ является метод биполярного кодирования с альтернативной инверсией (AMI - Alternate Mark Inversion). В нем применяются три уровня потенциала – +UВ, 0В и -UВ. Для кодирования логического нуля используется нулевой потенциал, а логическая единица кодируется либо положительным потенциалом, либо отрицательным, при этом потенциал каждой новой единицы противоположен потенциалу предыдущей (рисунок 6.1).

Рисунок 6.1 – Код AMI

Сравнительно простой в реализации код AMI частично решает проблемы наличия постоянной составляющей и отсутствия самосинхронизации, присущие коду NRZ при передаче длинных последовательностей единиц. В этом случае сигнал на линии представляет собой последовательность разнополярных импульсов с тем же спектром, что и у кода NRZ при передаче чередующихся нулей и единиц. Такой сигнал не имеет постоянной составляющей и его основная гармоника N/2 Гц (где N – битовая скорость передачи данных). Длинные же последовательности нулей так же нежелательны для кода AMI, как и для кодов NRZ, RZ и NRZI, т.к. при этом сигнал вырождается в постоянный потенциал с нулевой амплитудой.

При передаче различных последовательностей бит использование кода AMI приводит к более узкому спектру сигнала, чем для кода NRZ, а значит, и к более высокой пропускной способности линии. Например, при передаче чередующихся нулей и единиц основная гармоника f₀ имеет частоту N/4 Гц.

Кроме того код AMI предоставляет некоторые возможности по распознаванию ошибочных сигналов. Выявив нарушения очерёдности полярности сигналов, можно сделать вывод о ложном импульсе или исчезновении с линии корректного импульса.

Недостатком кода AMI является использование трех уровней сигнала, т.к. дополнительный уровень требует увеличения мощности передатчика примерно на 3 дБ для обеспечения достоверности приёма битов на линии. Данный недостаток присущ всем методам кодирования с несколькими (более двух) состояниями сигнала по сравнению с кодами, которые различают только два состояния.

Порядок выполнения:

1. Открыть рабочий лист Mathcad, созданный в предыдущих лабораторных работах.

2. Разработать Mathcad-функцию AMI-кодер.

3. Разработать Mathcad-функцию AMI-декодер.

4. Закодировать с помощью функции из п.2 поочередно входные последовательности данных, заданные в лабораторной работе №1:

· последовательность нулей;

· последовательность единиц;

· последовательность чередующихся нулей и единиц;

· текстовая строка.

5. Передать поочередно полученные кодовые последовательности с помощью модели канала, разработанной в лабораторной работе №2.

6. Декодировать поочередно полученные приемником сигналы с помощью функции из п.3.

7. С помощью Mathcad-функций berCalc() и serCalc() из лабораторной работы №1 вычислить интенсивность ошибки на бит (символ) для каждой последовательности.

8. Свести результаты работы в таблицу (приложение 1).

9. Оформить отчет в виде Mathcad-файла.

10. Сдать и защитить работу.

Содержание отчёта по лабораторной работе:

1. Номер название и цель лабораторной работы.

2. Задание к лабораторной работе.

3. Разработанные в лабораторной работе функции.

4. Результаты выполнения с пояснениями.

5. Выводы по лабораторной работе.

Контрольные вопросы:

1. Охарактеризуйте принцип AMI-кода.

2. Сравните код AMI поочередно с NRZ и NRZI.

3. В чем заключается основное преимущество кода AMI?

4. Как можно устранить недостатки, присущие описанным выше методам кодирования (NRZ, RZ, NRZI)?

5. Перечислите недостатки кода AMI.

Лабораторная работа №7

Биполярный импульсный метод кодирования

Цель работы: Изучение методов цифрового кодирования сигналов на примере биполярного импульсного кода. Исследование процесса передачи данных на физическом уровне.

Подготовка к лабораторной работе:

1. Повторить программирование в системе Mathcad.

2. Изучить соответствующие разделы в литературе [1-4].

Краткая теория:

Как уже было сказано выше, кроме потенциальных кодов в телекоммуникационных сетях используются и импульсные коды, в которых данные представлены полным импульсом или же его частью - фронтом. Наиболее простым случаем такого подхода является биполярный импульсный код, в котором единица представляется импульсом одной полярности, а ноль - другой (рисунок 7.1). Каждый импульс длится половину такта.

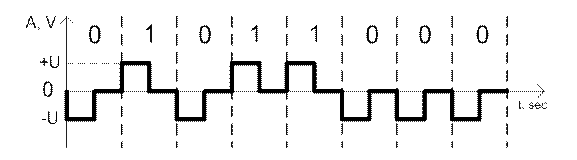
Рисунок 7.1 – Биполярный импульсный код

К достоинствам данного метода кодирования можно отнести отличную самосинхронизацию.

Недостатком является более широкий спектр по сравнению с потенциальными кодами (общий недостаток импульсных кодов). Например, при передаче всех нулей или единиц частота основной гармоники кода будет равна N Гц, что в два раза выше основной гармоники кода NRZ и в четыре раза выше основной гармоники кода AMI при передаче чередующихся единиц и нулей.

Из-за слишком широкого спектра биполярный импульсный код используется редко.

Порядок выполнения:

1. Открыть рабочий лист Mathcad, созданный в предыдущих лабораторных работах.

2. Разработать Mathcad-функцию Биполярный Импульсный кодер.

3. Разработать Mathcad-функцию Биполярный Импульсный декодер.

4. Закодировать с помощью функции из п.2 поочередно входные последовательности данных, заданные в лабораторной работе №1:

· последовательность нулей;

· последовательность единиц;

· последовательность чередующихся нулей и единиц;

· текстовая строка.

5. Передать поочередно полученные кодовые последовательности с помощью модели канала, разработанной в лабораторной работе №2.

6. Декодировать поочередно полученные приемником сигналы с помощью функции из п.3.

7. С помощью Mathcad-функций berCalc() и serCalc() из лабораторной работы №1 вычислить вероятность ошибки на бит (символ) для каждой последовательности.

8. Свести результаты работы в таблицу (приложение 1).

9. Оформить отчет в виде Mathcad-файла.

10. Сдать и защитить работу.

Содержание отчёта по лабораторной работе:

1. Номер название и цель лабораторной работы.

2. Задание к лабораторной работе.

3. Разработанные в лабораторной работе функции.

4. Результаты выполнения с пояснениями.

6. Выводы по лабораторной работе.

Контрольные вопросы:

1. Перечислите и кратко охарактеризуйте виды цифрового кодирования.

2. Какие требования предъявляются к цифровым кодам?

3. Опишите принцип биполярного импульсного кода.

4. Перечислите недостатки биполярного кода.

5. Каковы достоинства биполярного импульсного кода?

6. Сравните потенциальные и импульсные коды.

Лабораторная работа №8

Манчестерский метод кодирования

Цель работы: Изучение методов цифрового кодирования сигналов на примере манчестерского кода. Исследование процесса передачи данных на физическом уровне.

Подготовка к лабораторной работе:

1. Повторить программирование в системе Mathcad.

2. Изучить соответствующие разделы в литературе [1-3].

Краткая теория:

До недавнего времени наиболее распространенным в локальных сетях с технологией Ethernet или Token Ring был так называемый манчестерский код.

При манчестерском кодировании единиц и нулей используется перепад потенциала, то есть фронт импульса, таким образом, каждый такт делится на две части. Информация кодируется перепадами потенциала, происходящими в середине каждого такта, причем единица представляется перепадом от низкого уровня сигнала к высокому, а ноль – обратным перепадом (рисунок 8.1).

Рисунок 8.1 – Манчестерский код

В начале каждого такта может происходить служебный перепад сигнала, если нужно представить несколько единиц или нулей подряд.

Достоинства данного метода кодирования:

§ обладает хорошими самосинхронизирующими свойствами, так как сигнал изменяется, по крайней мере, один раз за такт передачи одного бита данных;

§ полоса пропускания манчестерского кода уже, чем у биполярного импульсного. В среднем ширина полосы манчестерского кода в полтора раза уже, чем у биполярного импульсного кода, а основная гармоника колеблется вблизи значения 3N/4;

§ нет постоянной составляющей, а основная гармоника в худшем случае (при передаче последовательностей нулей или единиц) имеет частоту N Гц, а в лучшем (при передаче чередующихся нулей и единиц) - N/2 Гц, как и у кодов AMI и NRZ.

Еще одно преимущество манчестерского кода перед биполярным импульсным кодом заключается в том, что в последнем для передачи данных используются три уровня сигнала, а в манчестерском – два.

Порядок выполнения:

1. Открыть рабочий лист Mathcad, созданный в предыдущих лабораторных работах.

2. Разработать Mathcad-функцию Манчестерский кодер.

3. Разработать Mathcad-функцию Манчестерский декодер.

4. Закодировать с помощью функции из п.2 поочередно входные последовательности данных, заданные в лабораторной работе №1:

· последовательность нулей;

· последовательность единиц;

· последовательность чередующихся нулей и единиц;

· текстовая строка.

5. Передать поочередно полученные кодовые последовательности с помощью модели канала, разработанной в лабораторной работе №2.

6. Декодировать поочередно полученные приемником сигналы с помощью функции из п.3.

7. С помощью Mathcad-функций berCalc() и serCalc() из лабораторной работы №1 вычислить вероятность ошибки на бит (символ) для каждой последовательности.

8. Свести результаты работы в таблицу (приложение 1).

9. Оформить отчет в виде Mathcad-файла.

10. Сдать и защитить работу.

Содержание отчёта по лабораторной работе:

1. Номер название и цель лабораторной работы.

2. Задание к лабораторной работе.

3. Разработанные в лабораторной работе функции.

4. Результаты выполнения с пояснениями.

5. Выводы по лабораторной работе.

Контрольные вопросы:

1. К какому виду кодов относится манчестерский?

2. Сравните потенциальные коды с импульсными.

3. Опишите принцип манчестерского кода.

4. Каковы достоинства и недостатки манчестерского кода?

5. Какова ширина полосы манчестерского кода?

6. Каким образом достигается самосинхронизация сигнала при манчестерском кодировании?

7. Какой метод кодирования предпочитается в сетях Ethernet в настоящее время?

Лабораторная работа №9

Дифференциальное Манчестерское кодирование

Цель работы: Изучение методов цифрового кодирования сигналов на примере дифференциального манчестерского кода. Исследование процесса передачи данных на физическом уровне.

Поиск по сайту: