 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Подготовка к лабораторной работе. 1. Повторить программирование в системе Mathcad
1. Повторить программирование в системе Mathcad.
2. Изучить соответствующие разделы в литературе [1-3].
Краткая теория
При дифференциальном манчестерском кодировании в течение битового интервала (времени передачи одного бита) уровень сигнала может меняться дважды. Обязательно происходит изменение уровня в середине интервала, этот перепад используется для синхронизации. Получается, что при передаче нуля в начале битового интервала происходит перепад уровней, а при передаче единицы такой перепад отсутствует. В этом случае единичный бит характеризуется отсутствием изменения напряжения по сравнению с уровнем напряжения во второй половине предшествующего бита. Изменение напряжения в начале бита означает, что это нулевой бит (рисунок 9.1).

Рисунок 9.1 – Дифференциальный манчестерский код
Данный метод обладает достоинствами и недостатками манчестерского кодирования.
Порядок выполнения:
1. Открыть рабочий лист Mathcad, созданный в предыдущих лабораторных работах.
2. Разработать Mathcad-функцию Дифференциальный манчестерский кодер.
3. Разработать Mathcad-функцию Дифференциальный манчестерский декодер.
4. Закодировать с помощью функции из п.2 поочередно входные последовательности данных, заданные в лабораторной работе №1:
· последовательность нулей;
· последовательность единиц;
· последовательность чередующихся нулей и единиц;
· текстовая строка.
5. Передать поочередно полученные кодовые последовательности с помощью модели канала, разработанной в лабораторной работе №2.
6. Декодировать поочередно полученные приемником сигналы с помощью функции из п.3.
7. С помощью Mathcad-функций berCalc() и serCalc() из лабораторной работы №1 вычислить интенсивность битовой (символьной) ошибки для каждой последовательности.
8. Свести результаты работы в таблицу (приложение 1).
9. Оформить отчет в виде Mathcad-файла.
10. Сдать и защитить работу.
Содержание отчёта по лабораторной работе:
1. Номер название и цель лабораторной работы.
2. Задание к лабораторной работе.
3. Разработанные в лабораторной работе функции.
4. Результаты выполнения с пояснениями.
5. Выводы по лабораторной работе.
Контрольные вопросы:
1. Опишите принцип дифференциального манчестерского кода.
2. В чем разница между манчестерским и дифференциальным манчестерским кодами?
3. К какому виду кодирования относится дифференциальный манчестерский код?
4. Каковы достоинства дифференциального манчестерского кода?
5. Каким образом достигается самосинхронизация сигнала при дифференциальном манчестерском кодировании?
Лабораторная работа №10
2B1Q метод кодирования
Цель работы: Изучение методов цифрового кодирования сигналов на примере кода 2B1Q. Исследование процесса передачи данных на физическом уровне.
Подготовка к лабораторной работе:
1. Повторить программирование в системе Mathcad.
2. Изучить соответствующие разделы в литературе [1-3].
Краткая теория:
На рисунке 10.1 представлен потенциальный код с четырьмя уровнями сигнала. Это код 2B1Q, название которого отражает его суть – каждые два бита (2B) передаются за один такт (1) сигналом, имеющим четыре состояния (Q - Quadra). Паре битов 00 соответствует потенциал -2,5B, паре 01 – потенциал
-0,833B, паре 11 – потенциал +0,833B, а паре 10 – потенциал +2,5B.
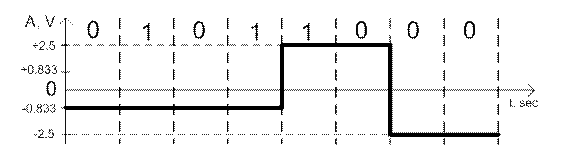
Рисунок 10.1 – Метод кодирования 2B1Q
При этом способе кодирования требуются дополнительные меры по борьбе с длинными последовательностями одинаковых пар битов, так как при этом сигнал превращается в постоянную составляющую. При случайном чередовании битов спектр сигнала в два раза уже, чем у кода NRZ, так как при той же битовой скорости длительность такта увеличивается в два раза. Таким образом, с помощью кода 2B1Q можно по одной и той же линии передавать данные в два раза быстрее, чем с помощью кода NRZI или AMI. Однако для его реализации мощность передатчика должна быть выше, чтобы четыре уровня чётко различались приёмником на фоне помех.
Для улучшения потенциальных кодов, типа 2B1Q, NRZI или AMI используются два метода. Первый метод основан на добавлении в исходный код избыточных битов, содержащих логические единицы. Очевидно, что в этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных. Исчезает также постоянная составляющая, а значит, ещё более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии, так как избыточные единицы пользовательской информации не несут.
Другой метод основан на предварительном «перемешивании» исходной информации таким образом, чтобы вероятности появления нулей и единиц на линии становились близкими по значению. Устройства, выполняющие такую операцию, называются скремблерами. При скремблировании используется известный алгоритм, поэтому приёмник, получив двоичные данные, передаёт их на дескремблер, который восстанавливает исходную последовательность битов.
Порядок выполнения:
1. Открыть рабочий лист Mathcad, созданный в предыдущих лабораторных работах.
2. Разработать Mathcad-функцию 2B1Q-кодер.
3. Разработать Mathcad-функцию 2B1Q-декодер.
4. Закодировать с помощью функции из п.2 поочередно входные последовательности данных, заданные в лабораторной работе №1:
· последовательность нулей;
· последовательность единиц;
· последовательность чередующихся нулей и единиц;
· текстовая строка.
5. Передать поочередно полученные кодовые последовательности с помощью модели канала, разработанной в лабораторной работе №2.
6. Декодировать поочередно полученные приемником сигналы с помощью функции из п.3.
7. С помощью Mathcad-функций berCalc() и serCalc() из лабораторной работы №1 вычислить интенсивность битовой (символьной) ошибки для каждой последовательности.
8. Свести результаты работы в таблицу (приложение 1).
9. Оформить отчет в виде Mathcad-файла.
10. Сдать и защитить работу.
Содержание отчёта по лабораторной работе:
1. Номер название и цель лабораторной работы.
2. Задание к лабораторной работе.
3. Разработанные в лабораторной работе функции.
4. Результаты выполнения с пояснениями.
5. Выводы по лабораторной работе.
Контрольные вопросы:
1. Перечислите и кратко охарактеризуйте способы представления информации в канале передачи данных.
2. Какие требования предъявляются к цифровым кодам?
3. Опишите принцип кода 2B1Q.
4. К какому виду кодирования 2B1Q относится?
5. Перечислите недостатки кода 2B1Q.
6. Как можно улучшить потенциальные коды?
7. Что представляют собой скремблер и дескремблер?
8. Насколько по сравнению с другими кодами необходимо увеличивать мощность передатчика для уверенного приема сигнала?
Лабораторная работа №11
MLT-3 метод кодирования
Цель работы: Изучение методов цифрового кодирования сигналов на примере кода MLT-3. Исследование процесса передачи данных на физическом уровне.
Подготовка к лабораторной работе:
1. Повторить программирование в системе Mathcad.
2. Изучить соответствующие разделы в литературе [1-3].
Краткая теория:
Код MLT-3 (Multi-Level Transition-3) – метод кодирования, использующий три уровня сигнала. Метод основывается на циклическом переключении потенциала. При передаче нулевого битового интервала уровень сигнала не меняется, а при передаче единицы меняется на следующий уровень по такой цепочке: +U, 0, –U, 0, +U, 0, –U и т.д. (рисунок 11.1).

Рисунок 11.1 – Кодирование MLT-3
Таким образом, максимальная частота смены уровней получается вчетверо меньше скорости передачи в битах (при последовательности сплошных единиц). Требуемая полоса пропускания оказывается меньше, чем при коде NRZ.
Порядок выполнения:
1. Открыть рабочий лист Mathcad, созданный в предыдущих лабораторных работах.
2. Разработать Mathcad-функцию MLT-3-кодер.
3. Разработать Mathcad-функцию MLT-3-декодер.
4. Закодировать с помощью функции из п.2 поочередно входные последовательности данных, заданные в лабораторной работе №1:
· последовательность нулей;
· последовательность единиц;
· последовательность чередующихся нулей и единиц;
· текстовая строка.
5. Передать поочередно полученные кодовые последовательности с помощью модели канала, разработанной в лабораторной работе №2.
6. Декодировать поочередно полученные приемником сигналы с помощью функции из п.3.
7. С помощью Mathcad-функций berCalc() и serCalc() из лабораторной работы №1 вычислить вероятность битовой (символьной) ошибки для каждой последовательности.
8. Свести результаты работы в таблицу (приложение 1).
9. Оформить отчет в виде Mathcad-файла.
10. Сдать и защитить работу.
Содержание отчёта по лабораторной работе:
1. Номер название и цель лабораторной работы.
2. Задание к лабораторной работе.
3. Разработанные в лабораторной работе функции.
4. Результаты выполнения с пояснениями.
5. Выводы по лабораторной работе.
Контрольные вопросы:
1. Сравните данный вид кодирования со всеми предыдущими.
2. Опишите принцип MLT-3-кода.
3. Перечислите достоинства и недостатки кода MLT-3.
4. Обладает ли код MLT-3 хорошими самосинхронизирующими свойствами? Если да, то, каким образом это достигается?
5. Какова ширина спектра сигнала при данном виде кодирования?
6. Сравните корректирующую способность описанных выше кодов. Поясните результаты сравнения.
Литература
1. Олифер В.Г., Олифер Н.А. Компьютерные сети. Принципы, технологии, протоколы: Учебник для вузов. 3-е изд. – СПб.: Питер, 2006. – 958 с.
2. Столлингс В. Компьютерные системы передачи данных, 6-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2002. – 928 с.
3. Блэк Ю. Сети ЭВМ: Протоколы, стандарты, интерфейсы: Пер. с англ. – М.: Мир, 1990. – 506 с.
ПРИЛОЖЕНИЕ 1
Таблица 1 – Вероятность ошибки на бит и на символ для различных методов кодирования
| Код | BER | SymbolER “txt” | |||
| “0” | “1” | “01” | “txt” | ||
| NRZ | |||||
| RZ | |||||
| NRZI | |||||
| AMI | |||||
| MLT-3 | |||||
| 2B1Q | |||||
| Биполярный импульсный | |||||
| Манчестерский | |||||
| Дифференциальный манчестерский |
Елена Викторовна Кокорева
Александр Федорович Ярославцев
Поиск по сайту: