АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение адсорбции Гиббса

Читайте также:
  1. Адсорбция на границе газ-жидкость. Изотерма Гиббса.
  2. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  3. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  4. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  5. Волна вероятности. Уравнение Шредингера
  6. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  7. Временное и стационарное уравнение Шредингера. Решения.
  8. Вязкость жидкости. Уравнение Ньютона. Закон Пуазейля
  9. Гармонические колебания и их характеристики. Дифференциальное уравнение свободных гармонических колебаний.
  10. Гипербола. Каноническое уравнение гиперболы и его свойства.
  11. Давление газа с точки зрения молекулярно-кинетической теории. Уравнение состояния идеального газа.
  12. Давление газа. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона). Изопроцессы.

Исходя из второго закона термодинамики американский ученый Гиббс в 70-х г. XIX в. вывел важное уравнение, связывающее величину адсорбции со способностью растворенного вещества изменять поверхностное натяжение раствора. Характеризует избыточную адсорбцию в зависимости от концентрации, температуры, изменении поверхностного натяжения.

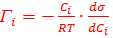- развернутая форма адсорбционного уравнения.

Где

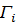- избыточная адсорбция i-го компонента,

– молярная концентрация в растворе,

- температура, при которой происходит адсорбция,

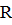- универсальная газовая постоянная,

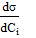- изменение поверхностного натяжения раствора при изменении концентрации на .

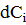В такой форме уравнение Гиббса применяется для разбавленных растворов.

Для концентрированных растворов концентрацию (С) заменяют на активность (а):

Он вывел его теоретически, в дальнейшем оно было подтверждено экспериментально Мак - Беном, Сазаки.

Проанализируем уравнение Гиббса.

Из уравнения видно, что влияние природы на адсорбцию заключено, в величине и знаке :

если то , т.е. наблюдается положительная адсорбция, т.е. i-тое вещество концентрируется на поверхности раствора,

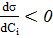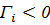если , то , т.е. наблюдается отрицательная адсорбция – вещество уходит с поверхности в раствор.

Для того чтобы рассчитать 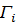по уравнению адсорбции Гиббса, надо знать , т.е. производную поверхностного натяжения от концентрации i-го компонента.

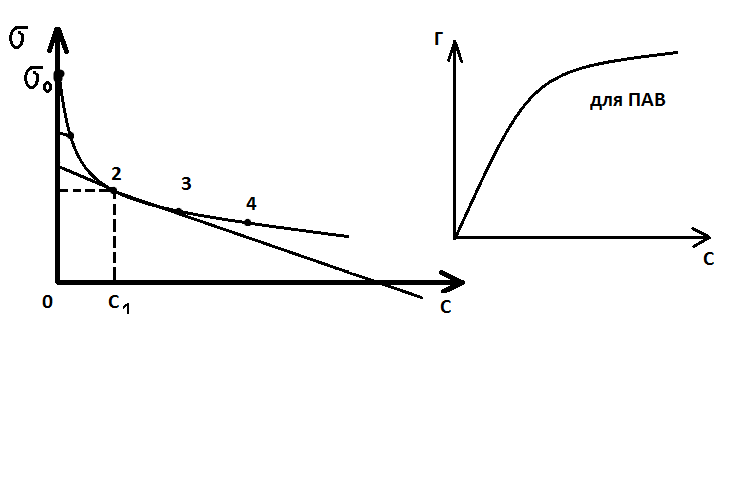
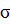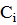Следовательно имея зависимость от С можно получить изотерму адсорбции данного компонента. Для этого нужно определить значение (при концентрации касательная в точке 1) в различных точках и подставить значения производных в уравнении адсорбции.

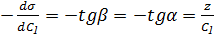, отсюда

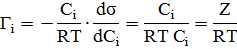
Так можно рассчитать значение адсорбции для любой концентрации и заполнить таблицу:

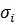
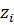
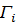
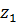
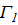
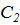
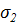
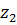
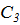
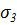
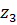
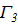
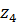
Эти данные позволяют построить изотерму адсорбции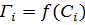

 

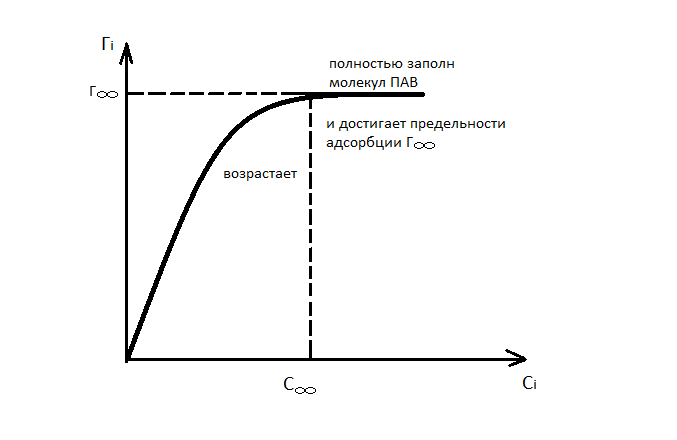
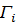– избыточная или Гиббсовская адсорбция представляет избыток вещества в поверхностном слое, на единицу поверхности по сравнению с его концентрацией в объеме фазы.


1 | 2 | 3 | 4 | 5 | 6 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.152 сек.)