 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ЭЛЕМЕНТЫ ТЕОРИИ ПОЗНАНИЯ
1.1. РОЛЬ ИЗМЕРЕНИЙ В ТЕОРИИ ПОЗНАНИЯ
Материалистическая концепция в естествознании, развивавшаяся великими представителями всех времен и народов, состоит в том, что объекты и явления окружающего мира существуют независимо от нас, от нашего сознания и восприятия этих объектов и явлений. Исходной материалистической предпосылкой является признание того, что материя, материальный мир первичны, а сознание, мысль вторичны. Это фундаментальное положение отнюдь не тривиально. Его утверждение проходило в острейшей борьбе философских течений и школ, не вполне завершившейся по настоящее время. Отстаивая материализм, В.И. Ленин в работе "Материализм и эмпириокритицизм" писал: "... в основе... материализма лежит признание внешнего мира..." Советской наукой, основанной на материалистических представлениях, это положение рассматривается как постулат, краеугольный камень марксистско-ленинского мировоззрения.
Объекты и явления окружающего мира являются для нас предметами познания. Познавательная деятельность ведется по линии многих наук, но, как было показано В.И. Лениным на примере физики, никакая наука не может двигаться вперед, отступая от материалистического понимания познания как отражения объективной природы, реально существующего материального мира.
Познавательная деятельность имеет свои законы. Суть их — в ленинском определении процесса познания: "От живого созерцания к абстрактному мышлению и от него к практике — таков диалектический путь познания истины, познания объективной реальности"*. Эта ленинская формула теории познания справедлива для всех наук, всех направлений познавательной деятельности. Но если, следуя ей, начать "разбирать, каким образом из незнания является знание, каким образом неполное неточное знание становится более полным и более точным"**, то мы неизбежно придем к пониманию важности получения количественной информации об изучаемых объетах.Она обеспечивает конкретность абстрактного мышления ивыход его результатов в практику.
Получают количественную информацию посредством измерений. Таким образом, измерения входят в процесс познания, а процедура получения измерительной информации является познавательной процедурой.
На получении точной измерительной информации, питающей абстрактное мышление, зиждутся успехи всех естественных наук. Д.И. Менделеев отмечал, что любая "наука начинается... с тех пор, как начинают измерять; точная наука немыслима без меры". Ему же принадлежит и другое важное замечание: "В природе мера и вес суть главные орудия познания".
В научной литературе теория познания называется ГНОСЕОЛОГИЕЙ (от древнегреческого yvosis — знание, познание и лoyos — речь, слово, учение или наука). Поскольку измерения являются инструментом познания, постольку наука об измерениях—МЕТРОЛОГИЯ (от древнегреческого нe т роv — мера и лoyos) относится к гносеологии, а исходные понятия метрологии являются элементами теории познания.
* Ленин В.И. Соч. - Т. 29. - С. 152, 153. ** ЛенинВ.И. Соч.—Т. 14.—С. 91.
1.2. ИЗМЕРЯЕМЫЕ ВЕЛИЧИНЫ
Предметом познания, как уже говорилось, являются объекты, свойства и явления окружающего мира. Таким объектом, например, является окружающее нас пространство, а его свойством — протяженность. Последняя может характеризоваться различными способами. Общепринятой характеристикой (мерой) пространственной протяженности служит длина. Однако протяженность реального физического пространства является сложным свойством, которое не может характеризоваться только длиной. Для полного описания пространства рассматривается его протяженность по нескольким направлениям (координатам) или используются еще такие меры, как угол, площадь, объем. Таким образом, пространство является многомерным.
Любые события и явления в реальном мире происходят не мгновенно, а имеют некоторую длительность. Это свойство окружающего нас мира качественно отличается от пространственной протяженности. Его также можно характеризовать по-разному, но общепринятой мерой здесь является время:
Свойство тел сохранять в отсутствии внешних воздействий состояние покоя или равномерного прямолинейного движения называется инертностью. Мерой инертности является масса.
Свойство тел, состоящее в том, что они нагреты до некоторого состояния, качественно отличается от предыдущего. Оно могло бы характеризоваться средней скоростью теплового движения молекул, но распространение получила мера нагретости тел, называемая термодинамической температурой.
Общепринятые или установленные законодательным путем характеристики (меры) различных свойств, общих в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальных для каждого из них называются физическими величинами. Кроме длины, времени, температуры, массы к физическим величинам относятся плоский и телесный угол, сила, давление, скорость, ускорение, электрическое напряжение, сила электрического тока, индуктивность, освещенность и многие другие. Все они определяют некоторые общие в качественном отношении физические свойства, количественные характеристики которых могут быть совершенно различными. Получение сведений об этих количественных характеристиках как раз и является задачей измерений.
Объектами измерений являются не только физические величины. Например, в экономике существует понятие стоимости — свойства, общего для всех видов товарной продукции, но в количественном отношении индивидуального для каждого из них. Другой пример — цена. В эпоху зарождения товарного обмена она имела натуральное выражение и определялась эквивалентным количеством продуктов питания, поголовьем рогатого скота и т.п. С появлением всеобщего эквивалента — денег — и переходом к товарно-денежным отношениям цена стала выражаться в денежных знаках. И стоимость, и цена являются мерами различных свойств товарной продукции. Они относятся не к физическим, а к экономическим величинам или, как их называют, экономическим показателям.
В сфере промышленного производства и в различных видах народнохозяйственной деятельности большое внимание уделяется качеству продукции. Оно определяется как совокупность ее свойств, обусловливающих удовлетворение определенных потребностей в соответствии с назначением продукции. Мерами этих свойств служат показатели качества. В КВАЛИМЕТРИИ (от латинского qualis — какой по качеству, и греческого mе т рio — измеряю) — разделе метрологии, посвященном измерению качества, различают следующие виды показателей качества продукции:
1. Показатели назначения характеризуют свойства продукции, определяющие основные функции, для выполнения которых она предназначена, и обусловливают область ее применения.
2. Показатели надежности характеризуют свойства безотказности, долговечности, ремонтопригодности и сохраняемости.
3. Показатели экономного использования сырья, материалов, топлива, энергии и трудовых ресурсов характеризуют свойства изделия, отражающие его техническое совершенство по уровню или степени потребляемых им сырья, материалов, топлива и трудовых ресурсов при эксплуатации.
4. Эргономические показатели характеризуют систему "человек — изделие" (в частности, "человек — машина") и учитывают комплекс гигиенических, антропометрических, физиологических и психологических свойств человека, проявляющихся в производственных и бытовых процессах.
5. Эстетические показатели характеризуют информационную выразительность, рациональность формы, целостность «композиции и совершенство производственного исполнения.
6. Показатели технологичности характеризуют свойства состава и структуры или конструкции продукции, определяющие ее приспособленность к достижению минимальных затрат при производстве, эксплуатации и восстановлении для заданных значений показателей качества продукции, объема ее выпуска и условий выполнения работ.
7. Показатели транспортабельности характеризуют приспособленность продукции к перемещению в пространстве (транспортировке), не сопровождающемуся ее использованием или потреблением.
8. Показатели стандартизации и унификации характеризуют насыщенность продукции стандартными, унифицированными и оригинальными составными частями, а также уровень унификации с другими изделиями.
9. Патентно-правовые показатели характеризуют степень обновления технических решений, использованных в продукции, их патентную защиту, а также возможность беспрепятственной реализации продукции в стране и за рубежом.
10. Экологические показатели характеризуют уровень вредных воздействий на окружающую среду, возникающих при эксплуатации или потреблении продукции.
11. Показатели безопасности характеризуют особенности продукции, обусловливающие при ее использовании безопасность обслуживающего персонала.
12. Обобщенным показателем эффективности использования продукции является интегральный показатель качества, который определяют как соотношение суммарного полезного эффекта от эксплуатации или потребления продукции и суммарных затрат на ее создание и эксплуатацию или потребление.
Внутри каждого вида можно выделить группы и отдельные показатели качества. Таким образом, качество, как и пространство, многомерно.
Переход к количественным методам исследований на основе измерительной информации в биологии, психологии, спорте, искусстве, медицине, педагогике, социологии и т. д. стал отличительной чертой нашего времени. Привычным стало измерение знаний учащихся, мастерства спортсменов и исполнителей художественных произведений, вдохновения, красоты, таланта и других свойств, общих в качественном, но индивидуальных в количественном отношении. В абстрактной математике широкое распространение получили меры неопределенности, значимости и многие другие.
Между измеряемыми величинами существуют связи и зависимости, выражаемые математическими соотношениями и формулами. Эти формулы и соотношения могут отражать законы природы, как, например, закон Ома

или второй закон Ньютона
F = т а,
могут быть определениями некоторых величин, например, плотности
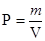
или интегрального показателя качества
Ки = ПS
3c+3п,
где ПS — суммарный полезный эффект от потребления продукции, а Зс и Зп — суммарные затраты на ее создание и потребление, либо, наконец, экспериментально или теоретически установленными соотношениями между несколькими величинами.
В подобных зависимостях одни величины выступают как основные, а другие — как производные от них. Опыт показал, что всю механику, например, можно изложить, используя всего три основных величины; всю теплотехнику —с помощью четырех основных величин; для изложения всей молекулярной физики достаточно пяти основных величин и т.д. Вся современная физика может быть построена на семи основных величинах. Выбор их в известном смысле является произвольным, но наиболее рационально основными физическими величинами выбрать такие, которые характеризуют фундаментальные свойства материального мира. В качестве гаковых в настоящее время установлены длина, масса, время, сила электрического тока, термодинамическая температура, количество вещества и сила света. С помощью этих и двух дополнительных величин — плоского и телесного углов — введенных исключительно для удобства, образуется все многообразие производных физических величин и обеспечивается описание любых свойств физических объектов и явлений.
В квалиметрии не принято деление показателей качества на основные и производные, Идея выражения одних показателей через другие воплощается здесь за счет выделения единичных показателей качества, каждый из которых относится только к одному из свойств продукции, и комплексных показателей, характеризующих сразу несколько ее свойств. Комплексные показатели выражаются через единичные подобно тому, как производные физические величины выражаются через основные.
1.3. КАЧЕСТВЕННАЯ ХАРАКРИСТИКА ИЗМЕРЯЕМЫХ ВЕЛИЧИН
Формализованным отражением качественного различия измеряемых величин является их размерность. Размерность обозначается символом dim, происходящим от слова dimension, которое в зависимости от контекста может переводиться, и как размерность.
Размерность основных физических величин обозначается соответствующими заглавными буквами. Для длинны, массы и времени, например,
dim l=L; dim m=M; dim t=T
При определении размерности производных величин руководствуются следующими правилами:
1. Размерности левой и правой частей уравнений не могут не совпадать, т.к. сравниваться между собой могут только одинаковые свойства. Объединяя левые и правые части уравнений, отсюда можно прийти к выводу, что алгебраически суммироваться могут только величины, имеющие одинаковые размерности.
2. Алгебра размерностей мультипликативна; т.е. состоит из одного единственного действия — умножения.
2.1. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость междузначениями величин Q, А, В, С имеет вид Q= A·B·C, то
dim Q= dim A · dim В · dimC.
2.2. Размерность частного при делении одной величины на другую равна отношению их размерностей, т.е. если Q = А/В, то
dim Q = dim A/dim В
2.3. Размерность любой величины, возведенной в некоторую степень, равна ее размерности в той же степени. Так, если Q =Аn, то

Например, если скорость определять по формуле v = 1/t, то dim v = dim I/dim t = L/T = LT-1. Если сила по второму закону Ньютона F = mа, где а = v/t — ускорение тела, то dim F = dim m · dim a = ML/Т2 = LMT -2.
Таким образом, всегда можно выразить размерность производной физической величины через размерности основных физических величин с помощью степенного одночлена:
dim Q= LaMbTg
где L, М, Т,... — размерности соответствующих основных физических величин; a, b, g,.. - показатели размерности. Каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, нулем. Если все показатели размерности равны нулю, то такая величина называется безразмерной. Она может быть относительной, определяемой как отношение одноименных величин (например, относительная диэлектрическая проницаемость), и логарифмической, определяемой как логарифм отношения этих величин (например, логарифм отношения мощностей или напряжений).
Итак, размерность является качественной характеристикой измеряемой величины. Она отражает ее связь с основными величинами и зависит от выбора последних. Как указывал М. Планк, вопрос об "истинной" размерности любой величины "имеет не более смысла, чем вопрос об "истинном" названии какого-либо предмета". По этой причине в гуманитарных науках, искусстве, спорте, квалиметрии, где номенклатура основных величин не определена, теория размерностей не находит пока эффективного применения. В физике, напротив, методами теории размерностей нередко удается получать важные самостоятельные результаты. Формальное применение алгебры размерностей иногда позволяет определить неизвестную зависимость между физическими величинами.
Пример 1. В результате наблюдений установлено, что при движении по окружности сила Р, прижимающая тело к опоре (рис. 1), в какой-то степени зависит от его скорости v, массы m и радиуса окружности г:
F= m a vвrу
Каков вид этой зависимости?
Решение. На основании алгебры размерностей
dimF = dimа m · dim в v · dimу r,
 но dim F = LMT-2;dim m = M; dim v = LT -1;dim r = L. Отсюда
но dim F = LMT-2;dim m = M; dim v = LT -1;dim r = L. Отсюда
LMT-2 = Mа (LT-1)ву= Lв+у MaT-в
Следовательно, показатели размерности удовлетворяют уравнениям:
в + у = 1; a = 1; — в= — 2,
решение которых: a = 1; в = 2; у = — 1. Таким образом,
F=mv2: r
К выводу этой зависимости на основе законов механики был близок Галилей но первым ее установил Гюйгенс.
Теория размерностей повсеместно применяется для оперативной проверки правильности сложных формул. Если размерности левой и правой частей уравнения не совпадают, т.е. не выполняется правило 1, то в выводе формулы, к какой бы области знаний она ни относилась, следует искать ошибку.
1.4. КОЛИЧЕСТВЕННАЯ ХАРАКТЕРИСТИКА ИЗМЕРЯЕМЫХ ВЕЛИЧИН
 Количественной характеристикой измеряемой величины служит ее размер. Получение информации о размере физической или нефизической величины является содержанием любого измерения. Простейший способ получения такой информации, позволяющий составить некоторое представление о размере измеряемой величины, состоит в сравнении его с другим по принципу "что больше (меньше)?" или "что лучше (хуже)?". Более подробная информация о том, на сколько больше (меньше) или во сколько раз лучше (хуже) иногда даже не требуется. Например, масса m1 на рис. 2 может быть намного, а может быть немного больше массы m2, но для решения вопроса о том, что легче, получаемой таким путем измерительной информации вполне достаточно. Подобным образом решаются многие задачи выбора: кто сильнее? что нагляднее? как проще? и т.п. При этом число сравниваемых между собой размеров может быть достаточно большим. Расположенные в порядке возрастания или убывания размеры измеряемых величин образуют шкалу порядка. Так, например, на многих конкурсах и соревнованиях мастерство исполнителей и спортсменов (или целых команд) определяется их местом, занятым в итоговой таблице. Последняя таким образом является шкалой порядка — формой представления измерительной информации, отражающей тот факт, что мастерство одних выше мастерства других, хотя и неизвестно, в какой степени (на сколько, или во сколько раз). Построив людей по росту, можно, пользуясь шкалой порядка, сделать вывод о том, кто выше кого, однако сказать на сколько выше, или во сколько раз — нельзя. Расстановка размеров в порядке их возрастания или убывания с целью получения измерительной информации по шкале порядка называется ранжированием.
Количественной характеристикой измеряемой величины служит ее размер. Получение информации о размере физической или нефизической величины является содержанием любого измерения. Простейший способ получения такой информации, позволяющий составить некоторое представление о размере измеряемой величины, состоит в сравнении его с другим по принципу "что больше (меньше)?" или "что лучше (хуже)?". Более подробная информация о том, на сколько больше (меньше) или во сколько раз лучше (хуже) иногда даже не требуется. Например, масса m1 на рис. 2 может быть намного, а может быть немного больше массы m2, но для решения вопроса о том, что легче, получаемой таким путем измерительной информации вполне достаточно. Подобным образом решаются многие задачи выбора: кто сильнее? что нагляднее? как проще? и т.п. При этом число сравниваемых между собой размеров может быть достаточно большим. Расположенные в порядке возрастания или убывания размеры измеряемых величин образуют шкалу порядка. Так, например, на многих конкурсах и соревнованиях мастерство исполнителей и спортсменов (или целых команд) определяется их местом, занятым в итоговой таблице. Последняя таким образом является шкалой порядка — формой представления измерительной информации, отражающей тот факт, что мастерство одних выше мастерства других, хотя и неизвестно, в какой степени (на сколько, или во сколько раз). Построив людей по росту, можно, пользуясь шкалой порядка, сделать вывод о том, кто выше кого, однако сказать на сколько выше, или во сколько раз — нельзя. Расстановка размеров в порядке их возрастания или убывания с целью получения измерительной информации по шкале порядка называется ранжированием.
Для облегчения измерений по шкале порядка некоторые точки на ней можно зафиксировать в качестве опорных {реперных). Знания, например, измеряют по ретерной шкале порядка, имеющей следующий вид: неудовлетворительно, удовлетворительно, хооошо, отлично. Точкам реперной шкалы могут быть поставлены в соответствие цифры, называемые баллами. Например, интенсивность землетрясений измеряется по двенадцатибалльной международной сейсмической шкале MSK-64 (табл. 1, шкала приведена с некоторыми сокращениями), сила ветра — по шкале Бофорта (табл. 2). По реперным шкалам измеряются сила морского волнения, степень торошения льда, чувствительность фотопленок, твердость минералов (минералогическая шкала твердости приведена в табл. 3) и многие другие величины. Особенно широкое распространение реперные шкалы получили в гуманитарных науках, спорте, искусстве и других областях. Где измерения еще не достигли высокого совершенства.
Недостатком реперных шкал является неопределенность интервалов между реперными точками. Поэтому баллы нельзя складывать, вычитать, перемножать, делить и т.п. Более совершенными в этом отношении являются шкалы, составленные из строго определенных интервалов. Общепринятым, например, является измерение времени по шкале, разбитой на интервалы равные периоду обращения Земли вокруг Солнца
Таблица 1
| Балл | Название землетрясения | Признаки |
| Незаметное Очень слабое | Отмечается только сейсмическими приборами Ощущается отдельными людьми, находящимися в состоянии покоя | |
| Слабое | Ощущается лишь небольшой частью населения | |
| Умеренное | Распознается по мелкому дребезжанию и колебанию предметов, посуды и оконных стекол, скрипу дверей и стен | |
| Довольно сильное | Общее сотрясение зданий, колебание мебели,трещины оконных стекол и штукатурки, пробуждение спящих | |
| Сильное | Ощущается всеми. Картины падают со стен,откалываются куски штукатурки, легкое повреждение зданий | |
| Очень сильное | Трещины в стенах каменных домов. Антисейсмические, а также деревянные постройки остаются невредимы | |
| Разрушительное | Трещины на крутых склонах и на сырой почве. Памятники сдвигаются с места или опрокидываются. Дома сильно повреждаются | |
| Опустошительное | Сильное повреждение и разрушение каменных домов | |
| Уничтожающее | Крупные трещины в почве. Оползни и обвалы. Разрушение каменных построек, искривление железнодорожных рельсов | |
| Катастрофа | Широкие трещины в земле. Многочисленные оползни и обвалы. Каменные дома совершенно разрушаются | |
| Сильная катастрофа | Изменения в почве достигают огромных размеров. Многочисленные обвалы, оползни, трещины. Возникновение водопадов, подпруд на озерах. Отклонение течения рек. Ни одно сооруже ние не выдерживает |
Таблица 2
| Балл | Название ветра | Признаки |
| Штиль | Дым идет вертикально | |
| Тихий | Дым идет слегка наклонно | |
| Легкий | Ощущается лицом, шелестят листья | |
| з | Слабый | Развеваются флаги |
| Умеренный | Поднимается пыль | |
| Свежий | Bызывает волны на воде | |
| сильный | Свистит в вантах, гудят провода | |
| Крепкий | На волнах образуется пена | |
| Очень крепкий | Трудно идти нротив вегра | |
| Шторм | ||
| Сильный шторм | Вырывает деревья с корнем | |
| Жестокий шторм | Большие разрушения | |
| Ураган | Опустошительное действие |
| Балл | Твердость |
| Меньше твердости талька Равна твердости талька или больше твердости талька, но меньше твердости гтпса. Равна твердости гипса или Больше твердости гипса, но меньше твердости известкового шпата. Равна твердости известкового шпата или больше твердости известкового шпата, но меньше твердости плавикового шпата. Равна твердости плавикового шпата или больше твердости плавикового шпата, на меньше твердости апатита. Равна твердости апатита или больше твердости апатита, но меньше твердости полевого шпата. Равна твердости полевого шпата или больше твердости полевого шпата, но меньше твердости кварца. Равна твердости кварца или больше твердости кварца, но меньше твердости топаза. Равна твердости топаза или больше твердости топаза, но меньше твердости корунда. Равна твердости корунда или больше твердости корунда, но меньше твердости алмеза. Равна твердости алмаза или больше твердости алмаза. |
(летоисчисление). Эти интервалы (годы) делятся на более мелкие (сутки), равные периоду обращения Земли вокруг своей оси. Сутки в свою очередь делятся на часы, часы на минуты, минуты на секунды. Такая шкала называется шкалой интервалов. По шкале интервалов можно уже судить не только о том, что один размер больше другого, но и о том, на сколько больше, т.е. на шкале интервалов определены такие математические действия, как сложение и вычитание.
При любом летоисчислении коренной перелом в ходе второй мировой войны произошел под Сталинградом спустя 700 лет после разгрома Александром Невским немецких рыцарей Ливонского ордена на льду Чудского озера. Но если поставить вопрос о том, "во сколько раз" позже наступило это событие, то окажется, что по нашему григорианскому стилю в  раза, по юлианскому календарю, отсчитываю щему время от "сотворения мира", — в
раза, по юлианскому календарю, отсчитываю щему время от "сотворения мира", — в  раза, по иудейскому, где время отсчитывается от "сотворения Адама”, - в
раза, по иудейскому, где время отсчитывается от "сотворения Адама”, - в  раза, а по магометанскому летоисчислению, начатому с даты бегства Магомета из Мекки в священный город Медину, где была основана первая мусульманская община, — в
раза, а по магометанскому летоисчислению, начатому с даты бегства Магомета из Мекки в священный город Медину, где была основана первая мусульманская община, — в 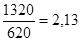 раза.
раза.
Следовательно, сказать по шкале интервалов во сколько раз один размер больше другого нельзя. Это объясняется тем, что на шкале интервалов известен масштаб, а начало отсчета может быть выбрано произвольно. Поэтому определить по шкале интервалов, чему равен тот или иной размер, невозможно.
Шкалы интервалов иногда получают путем пропорционального деления интервала между двумя реперными точками. Так, в температурной шкале Цельсия один градус является сотой частью интервала между температурой таяния льда, принимаемой за начало отсчета, и температурой кипения воды. В температурной шкале Реомюра этот же интервал разбит на 80 градусов, а в температурной шкале Фаренгейта — на 180 градусов, причем начало отсчета сдвинуто на 32° F в сторону низких температур. Соотношение между этими шкалами показано на рис. 3.
 Если в качестве одной из двух реперных точек выбрать такую, в которой размер не принимается равным нулю (что приводит к появлению отрицательных значений), а равен нулю на самом деле, то по такой шкале уже можно отсчитывать абсолютное значение размера и определять не только, на сколько один размер больше или меньше другого, но и во сколько раз он больше или меньше. Эта шкала называется шкалой отношений. Примером может служить температурная шкала Кельвина. В ней за начало отсчета принят абсолютный ноль температуры, при котором прекращается тепловое движение молекул. Более низкой температуры быть не может. Второй реперной точкой служит температура таяния льда. По шкале Цельсия интервал между этими реперами равен 273, 16° С (см, рис. 3). Поэтому на шкале Кельвина его делят, на равные, части, составляющие
Если в качестве одной из двух реперных точек выбрать такую, в которой размер не принимается равным нулю (что приводит к появлению отрицательных значений), а равен нулю на самом деле, то по такой шкале уже можно отсчитывать абсолютное значение размера и определять не только, на сколько один размер больше или меньше другого, но и во сколько раз он больше или меньше. Эта шкала называется шкалой отношений. Примером может служить температурная шкала Кельвина. В ней за начало отсчета принят абсолютный ноль температуры, при котором прекращается тепловое движение молекул. Более низкой температуры быть не может. Второй реперной точкой служит температура таяния льда. По шкале Цельсия интервал между этими реперами равен 273, 16° С (см, рис. 3). Поэтому на шкале Кельвина его делят, на равные, части, составляющие  интервала. Каждая такая часть называется Кельвином и равна градусу Цельсия, что значительно облегчает переход от одной шкалы к другой.
интервала. Каждая такая часть называется Кельвином и равна градусу Цельсия, что значительно облегчает переход от одной шкалы к другой.
Шкала отношений является наиболее совершенной из всех рассмотренных шкал. На ней определено наибольшее число математических операций: сложение, вычитание, умножение, деление. Но, к сожалению, построение шкалы отношений возможно не всегда. Время, например, может измеряться только по шкале интервалов.
В зависимости от того, на какие интервалы разбита шкала, один и тот же размер представляется ino-разному. Например, 0,001 км; 1 м; 100 см; 1000 мм — четыре варианта представления одного и того же размера. Их называют значениями измеряемой величины. Таким образом, значение измеряемой величины — это выражение ее размера в определенных единицах измерения. Входящее в него отвлеченное число называется числовым значением. Оно показывает, на сколько единиц измеряемый размер больше нуля или во сколько раз он больше единицы (измерения). Если0,5 кГд20 м, 8,12 руб., 6 баллов, 400 кормовых единиц, 100 т условного; топлива — некоторые значения измеряемых величин, то фигурирующие в них отвлеченные числа — числовые значения; этих величин. Таким образом, значение измеряемой величины Q определяется ее числовым значением q и некоторымразмером [Q], принятым за единицу измерения:
Q= q [Q]. (1)
Увеличение или уменьшение [Q] влечет за собой обратно пропорциональное изменение q. Поэтому значение, как и размер измеряемой величины, от выбора единиц измерения не зависит.
Словосочетания типа "размер длины'' или "размер массы" в метрологии не применяются. Не говорят и "величина длины" или "величина массы", так как длина и масса сами являются величинами. Принято говорить просто длина, масса, время, скорость. Например, масса составляет (или равна) 3кг, скорость 15 м/с.
1.5. ЕДИНИЦЫ ИЗМЕРЕНИЙ
Числовые значения измеряемых величин зависят от того, какие используются единицы измерений. Поэтому роль последних очень велика. Если допустить произвол в выборе единиц, то результаты измерений окажутся несопоставимыми между собой, т.е. нарушится единство измерений. Чтобы этого не произошло, единицы измерений устанавливаются по определенным правилам и закрепляются законодательным путем. Наличие законодательной метрологии отличает эту науку от других естественных наук (математики, физики, химии и др.) и направленно на борьбу с произволом в выборе таких решений, которые не диктуются объективными закономерностями, а принимаются по соглашению.
Совокупность единиц измерений основных и производных величин называется системой единиц. Не во всех областях измерений системы единиц сформировались окончательно и закреплены соответствующими законодательными актами. Наилучшим образом в этом отношении обстоят дела в области измерения физических величин.
В физике общие правили конструирования систем единиц были сформулированы Гауссом в 1832 г. Они сводятся к следующему:
1) выбираются основные физические величины,
2) устанавливаются единицы основных физических величин. Для этого какому-либо размеру каждой основной физической величины приписывается числовое значение, равное 1. Выбор этого размера является произвольным и определяется исключительно соображениями удобства его использовання в обиходе. Для обеспечения единства измерений все эти размеры, называемые единицами основных физических величин, должны быть закреплены законодательным путем. Обычно их называют просто основными единицами;
3) устанавливаются единицы производных физических величин, также называемые обычно просто производными единицами.
Пусть, например, производная физическая величина Q образуется путем перемножения двух основных величин А и В. Тогда, согласно выражению (1), значение Q можно выразить через значения А и В:
q[Q]=a[A]b[B],
а производная единица может быть выражена через основные единицы с помощью соотношения
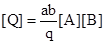
Если же производная величина Q образуется посредством деления основных величин А и В, то

и производная единица выражается через основные следующим образом:

В общем случае производные единицы выражаются через основные с помощью степенного одночлена
[Q]=k [A] a [B] b […] y …,
где коэффициент пропорциональности k полагается безразмерным, а а, b, y,... оказываются тогда уже известными показателями размерности. В последнее время к коэффициенту k стали предъявлять еще одно требование: он должен равняться 1. Получаемые при этом условии так называемые когерентные или согласованные системы единиц являются наиболее простыми и удобными в обращении.
В 1832 г. Гауссом была разработана система единиц, названная им абсолютной, с основными, единицами—миллиметр, миллиграмм, секунда. В дальнейшем по мере развития науки и техники возникали все новые и новые системы, пока их обилие не стало тормозом научно-технического прогресса. В этих условиях XI Генеральная конференция по мерам и весам в 1960 г. приняла Международную систему единиц физических величин, получившую у нас в стране сокращенное обозначение СИ (от начальных букв SI в словах Systeme international). Последующими Генеральными конференциями по мерам и весам в первоначальный вариант СИ внесены некоторые изменения, В Советском Союзе и странах Восточной Европы Международная система единиц является обязательной с 1 января 1980 г.
Основными единицами Международной системы являются:
метр (международное обозначение m; русское — м) — единица длины, равная пути, проходимому в вакууме светом за 1/299792458 долю секунды*;
килограмм (международное обозначение kg; русское — кг) — единица массы, равная массе международного прототипа килограмма;
секунда (международное обозначение s; русское — с) — единица времени, равная 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133;
ампер (международное обозначение А; русское — А) — единица силы электрического тока. Ампер равен силе неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызывал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2 · 107 Н;
кельвин (международное обозначение К; русское — К)— единица термодинамической температуры, равная 1/273,16 части термодинамической температуры тройной точки воды;
кандела (международное обозначение cd; русское—кд)— единица силы света. Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540 · 1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср;
моль (международное обозначение mol; русское—моль)— единица количества вещества. Моль равен количеству вещества, содержащему столько же структурных элементов (атомов, молекул или других частиц), сколько атомов содержится в 0,012 кг углерода-12.
Предусмотрены также две дополнительные единицы:
радиан (международное обозначение rad; русское — рад) — единица плоского угла, равная "внутреннему углу между двумя радиусами окружности, длина дуги между которыми равна радиусу;
стерадиан (международное обозначение sr; русское — ср) — единица телесного угла. Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности этой сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.
Производные единицы СИ образуются из основных и дополнительных по правилам образования когерентных производных единиц, т.е. связаны с ними соотношением
[Q]= мa · кг b -сg....
Некоторым из них даны названия в честь великих ученых: ньютон, герц, паскалъ, кулон, ом, сименс, тесла, беккерель и другие. Обозначения таких единиц, как международные, так и русские, пишутся с заглавной буквы.
Пример 2. Образовать производные единицы силы, давления, работы, мощности, электрических напряжения, сопротивления и проводимости.
Решение. 1. Так как dim F = LM Т'2 (см. 11), то [F] = м · кг · с2. Эта единица называется ньютон (Н):
Н = м · кг · с 2.
2. Давление р определяется силой, действующей при равномерной нагрузке на единицу поверхности. Поэтому dim р = L-1 МТ -2 и, следовательно, [р]=м-1 · кг · с. Эта единица называется паскаль (Па):
Па = м -1 · кг · с -2.
3. Работа А, совершаемая в направлении силы F, определяется по формуле: А = FL. Отсюда dim А = L2 МТ -2, а [А] = м2 · кг · с-2. Такая единица называется джоуль (Дж):
Дж = м2 · кг · с-2.
4. Мощность Р — это работа, совершаемая в единицу времени. Поэтому dimP = L2MT-3, a [P] = м2 · кг · с -3 Эта единица называется ватт (Вт):
Вт = м2 · кг · с -3.
5. Если электрическое напряжение U определить через мощность Р и силу I постоянного электрического тока, то dim U =L2MT-3I-1 и [U] = м2 · кг · с -3 · А-1. Единица электрического напряжения называется вольт (В):
В= м2 · кг · с-3 · А-1.
* При таком определении метра, принятом XVII Генеральной конференцией по мерам и весам в 1983 г., длина не может считаться основной физической величиной, так как выражается через скорость и время. По всей вероятности за этим решением XVII Генеральной конференции по мерам и весам должно последовать изменение структуры Международной системы единиц.
6. На основании закона Ома dim R = L2 МТ –3I-2. Отсюда [R] = м2 · кг · с -3 · А-2. Эта единица называется ом (Ом):
Ом = м2 · кг · с-3 · А-2.
7. Электрическая проводимость G — величина, обратная электрическому сопротивлению R. Поэтому dim G = L -2 М -1 Т3I2, а [G] = м -2 · кг-1 · с3 · А2. Единица электрической проводимости называется сименс (См):
См = м-2 · кг·с3 · А2.
Десятичные кратные и дольные единицы образуются с помощью множителей и приставок, наименования, происхождение и обозначения которых приведены в табл. 4.
К наименованию единицы допускается присоединять только одну приставку (например, пикофарада, а не микромикро-фарада). У единиц, образованных как произведение или отношениенескольких единиц, приставку присоединяют, как правило, к наименованию первой единицы, например, килопаскаль — секунда на метр (кПа · с/м), а не паскаль—килосекунда на метр. Кратные и дольные единицы выбирают обычно таким образом, чтобы числовое значение величины находилось в диапазоне от 0,1 до 1000 (например, для длины L = 7,5 Х 10 -s м = 75 мкм = 0,075 мм = 75000 нм следует выбрать 75 мкм, так как в других случаях числовое значение выходит за пределы указанного диапазона). От этого правила отступают только при составлении таблиц числовых значений одной и той же величины или при сопоставлении этих значений в одном тексте, а также в тех областях, где традиционно применяется конкретная единица (например, линейные размеры на машиностроительных чертежах всегда выражаются в миллиметрах).
Поиск по сайту: