Параметры акустических свойств горных пород

Скорости распространения упругих волн зависят в первую очередь от упругих параметров горной породы и от характера деформирования среды.

Если

< 0,2 ¸ 0,3 (6.1)

где d – поперечный размер образца горной породы и λ – длина волны) – в породе распространяются только продольные волны (случай «идеального стержня»). В этом случае скорость продольной волны

, (6.2)

где Е_д – модуль упругости Юнга, измеренный динамическим методом, Па;

r – плотность породы, кг/м³.

Если

> 0,8 ¸ 1 (6.3)

– в породах распространяются только продольные и поперечные волны (случай «массива»). Тогда

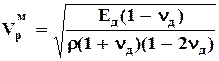, (6.4)

где n_д – коэффициент Пуассона, измеренный динамическим методом, ед.;

, (6.5)

где G_д – модуль всестороннего сжатия, измеренный динамическим методом, Па;

Если

= 0,3 ¸ 0,8 (6.6)

– в породах распространяются продольные, поперечные и поверхностные волны, причем при небольших удалениях от источника колебаний – продольные «стержневые», а с удалением – они исчезают и формируются продольные «массива».

В этом случае скорость поверхностной волны Рэлея

(6.7)

При n_д=0,25 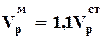, 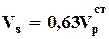и , т.е. можем констатировать, что

На величину скорости распространения волн влияют: пористость и трещиноватость породы (с увеличением пористости скорости уменьшаются), температура (у сухих пород с ростом температуры скорость монотонно возрастает, а у влажных пород при замерзании воды скорость резко возрастает), слоистость (скорость распространения волн вдоль слоистости на 10 ¸ 30% больше, чем перпендикулярно слоистости).

Приведем значения скорости продольных волн, м/с для некоторых веществ и пород: вода – 1485, воздух – 331, лед – 3200 ¸3300, известняк – @5000, песчаник – 2000 ¸3500, сланцы – @2000, масло трансформаторное – 1420.

Акустическое сопротивление

z = р×V, кг/м²·с (6.8)

определяет способность горных пород отражать и преломлять упругие волны и является отношением давления волны р к мгновенной скорости колебания частиц V.

Коэффициент поглощения. Амплитуда колебаний частиц в горной породе по мере удаления от источника акустических волн уменьшается по причине поглощения энергии на трение частиц, рассеивание энергии на порах, трещинах и других неоднородностях породы.

, (6.9)

где А_i и А₀ соответственно амплитуда волны на удалении r_i от источника;

Q – коэффициент поглощения.

Для однородных тел поглощение акустических волн определяется вязкостью и теплопроводностью тел. Как и для жидкостей, в этом случае зависимость коэффициента поглощения Q упругой продольной волны от частоты ω = 2 πf

, (6.10)

где – коэффициент вязкости (внутреннее трение породы), Па·с.

Коэффициент поглощения всегда больше в тех породах, в которых скорость упругих колебаний меньше.

Вообще для горных пород Q = (0,05 ¸ 0,3) 1/м, т.е. на расстоянии 3 ¸ 20 м от источника амплитуда (энергия) волны уменьшается в e = 2,7 раз.

Коэффициент отражения. Коэффициентом отражения К_э называют отношение амплитуды (энергии) отраженной волны А₀ к амплитуде (энергии) падающей волны А_п на границе раздела двух сред.

(6.11)

Например, на границе раздела воздух – порода теряется 99,98% энергии волны; вода – порода – 68%; порода – порода – около 14%.

На рисунке 6.1 представлены различные случаи преломления и отражения упругих волн на границе раздела двух сред.

Угол падения δ_п и угол преломления ψ упругой волны, проникшей в горную породу подчиняются закону Снеллиуса, согласно которому эти углы находятся в определенном соотношении со скоростью упругой волны в первой V₁ и второй V₂ средах

= (6.12)

Отношение V₁/V₂ = n называется коэффициентом преломления упругой волны.

Так как скорости различных типов волн различны, в результате прохождения упругой волны в породе происходит ее разделение по направлениям на продольные и поперечные.

Если упругая волна падает на границу раздела перпендикулярно, происходит только отражение. При угле падения δ_п > 0 происходит как отражение, так и преломление упругой волны. Постепенно увеличивая угол δ_п , можно добиться такого момента, когда произойдет полное внутреннее отражение сначала продольной, а затем и поперечной волны.

Поиск по сайту: