Теории прочности пород

Прочность породы определяется величиной критических напряжений, при которых происходит ее разрушение. Эти напряжения различны для разных пород и разных способов приложения нагрузки. Они называются пределы прочности (временное сопротивление). Различают пределы прочности пород при сжатии σ_вс, растяжении σ_вр, сдвиге τ_сдв, изгибе σ_изг и т.д.

Разрушение – это разрыв связей между атомами в кристаллической решетке.

Как показывают расчеты, предел прочности при растяжении должен быть равен 1 · 10⁴ МПа.

Однако в связи с тем, что реальные тела обладают множеством дефектов, значения предела прочности в сотни тысяч раз меньше теоретического значения.

Дефекты могут быть различные. В кристалле – это точечные (вакансии) и линейные (дислокации) искажение кристаллической решетки. В породе – границы зерен (плоскостные) и поры (объемные искажения) и нарушения строения породы.

В зависимости от масштаба разрушения породы преобладают те или иные дефекты.

Существует несколько масштабов (уровней) разрушения пород. Мегаскопический уровень разрушения характерен для взрывания массивов пород, сдвижений и обвалов их. В том случае наиболее сильно на разрушаемости сказываются крупные трещины.

Более мелкие трещины, поры, контакты между агрегатами зерен предопределяет разрушение макроскопическое – выемочными агрегатами (экскаваторами, комбайнами), буровыми инструментами.

Микроскопический уровень разрушения характерен для измельчения полезных ископаемых в мельницах и, частично, при бурении скважин. На этой стадии происходит разрыв связей в кристаллах и зернах. При этом существенную роль играют дислокации и вакансии.

Разрушение пород имеет либо хрупкий, либо пластичный характер. При хрупком разрушении происходит отрыв атомов друг от друга по всей плоскости разрушения, на что требуются большие усилия, чем при пластическом.

Мелкие трещины, поры, неоднородности, плоскости ослабления предопределяют преобладающий хрупкий характер разрушения горных пород, поэтому механизм их разрушения может быть описан посредством теории хрупкого разрушения, согласно которой решающее значение для начала разрушения имеют критические трещины в объеме твердого тела.

На краях трещины обычно возникают напряжения, значительно превышающие средние напряжения σ. Это явление называется концентрацией напряжений. Так, при длине трещины 2ℓ и радиусе ее закрепления на конце r (рисунок 4.16) напряжения на краю трещины равны

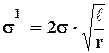
Рисунок 4.16 – Концентрация напряжений на краях трещины длиной 2ℓ и с радиусом закругления r (числа указывают кратность превышения напряжений σ¹ над σ):

а – при нагружении перпендикулярно трещине;

б – при нагружении параллельно ей.

Как только напряжение σ¹ достигнет определенного значения, трещина начнет развиваться, преодолевая при этом молекулярные силы сцепления (производя работу W_s, пропорциональную удельной поверхностной энергии е_s данного тела)

,

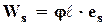где φℓ – площадь двух поверхностей трещины, приходящаяся на единицу поперечного размера породы.

Упругая энергия, запасенная в породе в результате действия внешней нагрузки и необходимая для образования трещины

, (4.24)

Трещина будет расти, если

. (4.25)

Отсюда предел прочности при растяжении

. (4.26)

При действии сжимающей нагрузки трещины смыкаются и на их поверхности появляются силы трения. В том случае предел прочности на сжатие больше предела прочности при растяжении σ_вс > σ_вр и их отношение подчиняется уравнению

, (4.27)

где tqφ – коэффициент внутреннего трения (tqφ = 0,2…2).

Например, для гранита σ_вс = 141 МПа, σ_вр = 11 МПа, 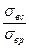= 13, песчаника кварцевого σ_вс = 164 МПа, σ_вр = 6,6 МПа, 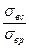= 26.

На основании теории хрупкого разрушения получаем 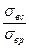= 5…17, что в ряде случаев близко к значениям, полученным экспериментально.

Кинетическая (термофлуктуационная) теория разрушения твердых тел, разработанная академиком С.Н. Журковым построена на том, что разрушение в некоторой зоне не является каким-то критическим состоянием тела. В соответствии с этой теорией в твердых телах непрерывно идет процесс накопления повреждений, которое приводит к полному разрушению тел. Время существования тела при действии нагрузки в не разрушенном состоянии определяется по следующей формуле

, (4.28)

где t_o – константа, совпадающая по порядку с периодом колебаний атомов и не зависящая от химического состава и структуры тела (t_o≈10^-12с);

U_o – энергия активации процесса разрушения, структурно-нечувствительная величина (для гранитов U_o ≈ 2,9 ∙ 10^-19 Дж; для кварцитов U_o ≈ 5,8 ∙ 10^-19 Дж);

V – активационный объем, зависящий от структуры тела и составляющий 10³…10⁴ атомных объемов (для гранитов V = 1,5 ∙ 10^{-27 м3}, для кварцитов V = 1,9 ∙ 10^{-27 м3});

kТ –- мера энергии тепловых флуктуаций;

k – постоянная Больцмана k = 1,38 ∙ 10^-23 Дж/к;

Т – абсолютная температура тела.

Предел прочности при растяжении равен

, (4.29)

т.е. предел прочности зависит от параметров U_o и V, температуры тела и длительности действия на него нагрузки.

Эксперименты, проведенные на породах, подтверждают снижение прочности с увеличением длительности действия нагрузки (рисунок 4.17).

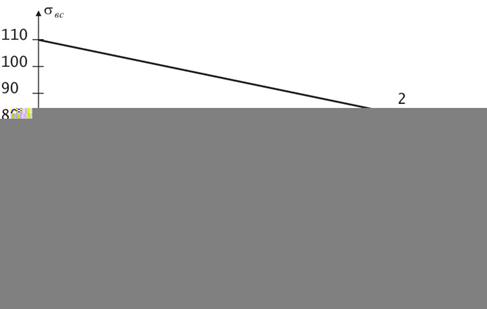Рисунок 4.17 – Кривые длительной прочности песчанистого сланца Донбасса (1) и известняка (2)

Прочность пород, соответствующая той или иной длительности действия нагрузки, называется их длительной прочностью σ_дл. С увеличением времени действия нагрузки величина длительной прочности σ_дл падает по кривой, асимметрически приближаясь к некоторому предельному значению, называемому пределом длительной прочности σ_∞. Предел длительной прочности для многих пород равен σ_∞ = (0,7…0,8) σ_вс.

Для оценки прочности горных пород в случае сложного напряженного состояния используют критерии, позволяющие заменить сложное напряженное состояние одноосным напряженным состоянием, для которого пределы прочности могут быть определены путем теоретических исследований, либо путем эксперимента.

Горные породы в подавляющем большинстве можно отнести к хрупким, поэтому при расчетах можно использовать теорию Сен-Венана (2 теория прочности) – теорию наибольших линейных деформаций. Если наибольшая линейная деформация достигла предельного значения, то напряженное состояние считается опасным.

, (4.30)

где μ – коэффициент Пуассона.

Для оценки разрушения пластичных можно применять теорию наибольших касательных напряжений (теория Кулона; третья теория прочности).

Напряженное состояние считается опасным, если наибольшие касательные напряжения достигли предельного значения.

(4.31)

Экспериментальная проверка этой гипотезы показала, что для пластичных материалов она приводит, в общем, к удовлетворительным результатам. Переход от упругого состояния к пластическому действительно с достаточной точностью определяется разностью между наибольшим и наименьшим из главных напряжений и слабо зависит от промежуточного главного напряжения σ₂. Наложение всестороннего давления на любое напряженное состояние не меняет величины наибольших касательных напряжений τ_max и, следовательно, не оказывает влияние на возникновение пластических деформаций. В частности, при всестороннем гидростатическом давлении τ_max обращается в нуль, следовательно, в материале не возникают пластические деформации. Наложение всестороннего давления влияет не на условие пластичности, а на условия разрушения. Граница разрушения отодвигается, и материал приобретает способность пластически деформироваться без разрушения, что объясняет поведение горных пород при определенных условиях.

Рассмотрим э нергетическую теорию прочности (4 теория прочности) Представим напряженное состояние (рисунок 4.19)в виде двух напряженных состояний: всестороннее растяжение, где и во втором напряженном состоянии, где по граням элемента действуют напряжения σ₁ – σ_о, σ₂ – σ_о, σ₃ – σ_о.

Первое напряженное состояние вызывает изменение объема элемента без изменения формы (куб до деформации остается кубом и после деформации), второе напряженное состояние вызывает изменение формы элемента (куб превращается в параллелепипед) без изменения объема.

Напряженное состояние считается опасным, если удельная потенциальная энергия изменения формы достигла предельного значения.

Эквивалентные напряжения определяются по формуле

(4.32)

Эта теория хорошо согласуется с экспериментом. Кроме того, перестановка местами индексов напряжений 1, 2, 3 в выражении не меняет величины эквивалентных напряжений.

К вопросу прочности, согласно теории прочности Мора, можно подойти и с других позиций – с позиций упрощенной систематизации экспериментальных данных.

Для хрупких тел, к которым относятся стекло, бетон, горные породы, критерий разрушения может быть сформулирован в принципе так же, как и критерий пластичности, в виде некоторого соотношения между компонентами тензора напряжений

. (4.33)

Если , то материал не разрушается. При выполнении условия (4.33) хотя бы в одной точке – происходит локальное разрушение. Под локальным разрушением понимают либо разрыв, разрушение и срез некоторых структурных элементов, либо появление зародышевой трещины или слияние с трещинами, возникшими в соседних точках, где выполняется условие (4.33). Область локального разрушения служит источником концентрации напряжений, поэтому вероятно использование новых очагов разрушения по соседству с уже возникшими.

Условие Мора: разрушение происходит тогда, когда на некоторой площадке величина касательного напряжения достигает критического значения, зависимо от действующего на этой площадке нормального напряжения

. (4.34)

Это условие (4.34) необходимо записать в зависимости от главных напряжений. Для этого воспользуемся геометрическим представлением напряженного состояния в виде круговой диаграммы Мора. При объемном напряженном состоянии, с учетом принятых обозначений, можно построить три окружности Мора (рисунок 4.18).

Точка, соответствующая определенному напряженному состоянию, с координатами σ_n, τ_n лежит в заштрихованной области, т.е. не может выйти за пределы большого круга, построенного на напряжениях σ₂ и σ_4.

Рисунок 4.18 – Круговая диаграмма для объемного напряженного состояния

Предположим, что мы располагаем испытательной машиной, на которой в образце можно создавать любые напряженные состояния с пропорциональным изменением всех компонент. Выберем некоторое напряженное состояние и будем одновременно увеличивать все компоненты. При некоторых значениях напряжений напряженное состояние станет предельным. Образец либо разрушится, либо в нем возникнут пластические деформации. Начертим один из наибольших кругов Мора для этого напряженного состояния (круг 1, рисунок 4.19).

На образце из того же материала проводим испытание при другом напряженном состоянии, добиваемся, что напряженное состояние становятся предельным (круг 2, рисунок 4.19).

В результате испытаний получаем семейство кругов Мора для различных предельных состояний. Вычеркиваем их общую огибающую кривую (рисунок 4.19). Эта огибающая кривая является единственной, независимо от главных напряжений σ₂. Это основное допущение в этой теории прочности.

Форма огибающей предельных кругов Мора зависит от свойств материала и является механической характеристикой материала. Проверка прочности проводится достаточно просто. Если окружность большого круга Мора не касается предельной кривой, разрушение не произойдет. Если круг Мора коснется огибающей кривой, то происходит локальное разрушение.

Часто проводят испытания на растяжение, сжатие, строят аппроксимирующую предельную огибающую в виде касательной к двум окружностям и тогда условие прочности принимает вид

, (4.35)

где σ_вр – временное сопротивление (предел прочности) при растяжении;

σ_вс – временное сопротивление (предел прочности) при сжатии.

Рисунок 4.19 – Огибающая кривая

Основное ограничение, которое накладывается на применение теории Мора, связано с неточностью определения огибающей кривой в условиях всестороннего растяжения. Это ограничение не столь существенно, поскольку напряженное состояние такого рода при решении практических задач встречается редко. Недостаточно известен вид огибающей кривой в области всестороннего сжатия. Здесь вследствие принятых упрощений возможны погрешности. Наилучшие результаты расчетная формула (4.35) дает для напряженных состояний при σ₁ > 0, σ₃ < 0. Тогда предельный круг Мора располагается в интервале между предельными кругами при растяжении и сжатии.

Подход Мора хорош тем, что позволяет объяснить относительную условность деления материалов на пластичные и хрупкие.

Для одного и того же материала можно построить две огибающие предельных кругов Мора. Первая огибающая характеризует переход от упругого состояния к пластическому. Эта огибающая представляет собой прямую, параллельную оси σ (рисунок 4.20). Вторая огибающая соответствует разрушению образца (кривая 2).

Для пластичного материала прямая 1 в правой части диаграммы (рисунок 4.20, а) проходит ниже кривой 2. Это означает, что при обычном испытании образца на растяжение круг Мора 3 по мере увеличения растягивающего напряжения σ, сначала пересечет прямую 1. В образце возникнут пластические деформации. Затем круг 3 коснется кривой 2. Образец разрушится.

Рисунок 4.20 – Огибающие кривые для пластичных (а) и хрупких (б) материалов

В настоящее время паспортом прочности горных пород называют кривую, огибающая все круги напряжений для предельных состояний (рисунок 4.21). При исследовании напряженного состояния в горном массиве сжимающие напряжения считают положительными.

Рисунок 4.21 – Огибающая кривая предельных напряженных состояний: 1 – всестороннее неравномерное растяжение; 2 – одноосное растяжение; 3 – чистый сдвиг; 4 – одноосное сжатие; 5 – всестороннее неравномерное сжатие; σ_вс – всестороннее равномерное сжатие; σ_вр – всестороннее равномерное растяжение

Положение огибающей кривой относительно начала координат характеризует степень хрупкости или вязкости пород.

Рисунок 4.22 – Огибающие кривые для различных материалов: а – сыпучих; б – хрупких; в – пластичных.

Проводят испытание образца на растяжение, сжатие и при объемном сжатии, строят огибающую кривую (рисунок 4.23). Основные параметры, определяемые по паспорту прочности:

- предельное сопротивление чистому сдвигу (срезу) τ_с (сцепление С_о) и соответствующий угол внутреннего трения φ_о (коэффициент внутреннего трения tqφ_o);

- условное сцепление С при различных напряжениях σ, τ и соответствующий угол внутреннего трения (коэффициент внутреннего трения tqφ), эти параметры – переменные величины.

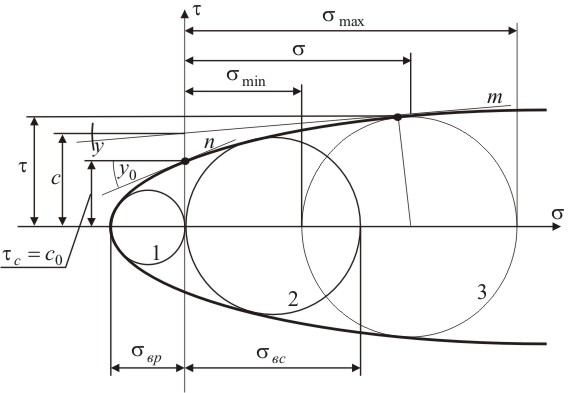
К огибающей кривой в точке ее пересечения с осью τ переводим касательную nn. Координата точки пересечения касательной nn с осью τ определяет предельное сопротивление материала при чистом сдвиге, угол между горизонтальной линией и касательной nn – угол внутреннего трения.

Рисунок 4.23 – Паспорт прочности горной породы: 1 – круг одноосного растяжения; 2 – круг одноосного сжатия; 3 – круг при объемном сжатии.

Касательная mm к огибающей в любой точке с координатами (σ; τ) составляет с горизонталью угол φ – угол внутреннего трения, координата точки пересечения касательной с осью τ, С – условное сцепление.

Метод построения паспорта прочности по данным определения пределов прочности при объемном сжатии, одноосном сжатии и растяжении следующий.

Для построения паспорта используют результаты определения пределов прочности при объемном сжатии не менее чем при трех различных значениях бокового давления. По значению и бокового давления строят семейство полуокружностей радиусами с координатами центров ().

Строят круги напряжений при одноосном растяжении и сжатии радиусами с координатами центров () и (). Проводят плавную кривую, огибающую все пять полуокружностей (рисунок 4.23).

Метод построения паспорта прочности по данным определения пределов прочности при срезе со сжатием, одноосном сжатии и растяжении таков: по совокупности парных значений нормальных σ_α и касательных τ_α напряжений, определенных при испытании на срез в координатах σ, τ отмечают точки 1, 2, 3 соответствующие углам α = 25⁰, 35⁰, 45⁰ наклона призм (рисунок 4.24).

Рисунок 4.24 – Паспорт прочности при испытании на растяжение, сжатие, сдвиг

Строят круги напряжений при растяжении и сжатии, проводят плавную кривую, огибающую полуокружности и проходящую через точки 1, 2, 4.

Расчетный метод построения паспорта прочности по данным определения пределов прочности при одноосном сжатии и растяжении предусматривает определение координат точек огибающей кривой расчетным путем по результатам испытаний при одноосном растяжении и сжатии по эмпирическому уравнению

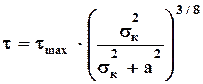, (4.36)

где τ_max – максимальное сопротивление породы срезу (сдвигу), при гипотетически полностью закрывшихся под действием нормального давления трещинах и порах;

σ_к – нормальное напряжение относительно начала координат, перенесенного в точку пересечения огибающей кривой;

а – параметр формы огибающей кривой.

Для удобства расчета и табулирования, уравнение огибающей кривой представляют в безразмерных координатах ℓ и К

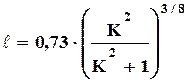, (4.37)

где ℓ – безразмерная координата соответствующая касательным напряжениям, ;

К – безразмерная координата, соответствующая нормальному напряжению.

, (4.38)

σ_о – значение параметра переноса начала координат.

Вводятся безразмерные радиусы предельных кругов Мора для одноосного растяжения q₁ и одноосного сжатия q₂, которые связаны отношением

Значение параметра огибающей кривой определяется по формуле

Параметр переноса начала координат

. (4.39)

Координаты σ и τ точек огибающей кривой определяют по формулам

; (4.40)

Для построения кривой вычисляют координаты не менее 10 точек, строят кривую.

Рисунок 4.25 – Паспорт прочности, построенный расчетным способом

Предельное сопротивление срезу τ_о (сцепление С_о) определяют как ординату точки пересечения огибающей с осью τ, а соответствующий угол трения φ_о, как угол наклона касательной nn к кривой в этой точке.

Условное сцепление С в любой точке огибающей кривой определяют как ординату точки пересечения касательной к огибающей в точке (σ, τ) с осью τ; угол внутреннего трения

. (4.41)

Условное сцепление С_1-2 в заданном диапазоне напряжений (σ₁…, σ₂) или (τ₁, …, τ₂) определяют как ординату точки пересечения прямой, проведенной через соответствующие точки огибающей, с осью τ и соответствующий угол внутреннего трения φ_1-2 как угол между этой прямой и осью σ.

. (4.42)

Рисунок 4.26 – Упрощенный метод построения паспорта прочности горных пород

К этим окружностям проводим касательную, которая будет являться огибающей предельных кругов Мора.

Уравнение этой прямой и есть паспорт прочности

. (4.43)

Поиск по сайту: