 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
по теоии вероятностей
Опр.: Распределение называется абсолютно непрерывным, если её ф.р. представима в виде Fx(x)= 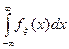 , где fx (x)≥ 0 и
, где fx (x)≥ 0 и 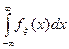 =1, fx (x) – плотность распределения
=1, fx (x) – плотность распределения
Свойства:
1.  Fx(x) – является непрерывной, п.в. дифференцируемой, при этом F’x(x)= f x(x), т.о., ф.р. является первообразной для плотности.
Fx(x) – является непрерывной, п.в. дифференцируемой, при этом F’x(x)= f x(x), т.о., ф.р. является первообразной для плотности.
2. P(x=x)=0 "xÛ P(a≤x≤b)= P(a<x≤b)= P(a≤x<b)= P(a<x<b).
3. P(a≤x<b)= Fx(b)-Fx(a)= 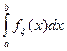 - площадь криволинейной трапеции (Геометрический смысл вероятности)
- площадь криволинейной трапеции (Геометрический смысл вероятности)
4. "BÌ B, P(x=B)= 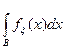 , dx – мера Лебега.
, dx – мера Лебега.
(Продолжение на след листочке)
Индивидуальные задания
по теоии вероятностей
Учебно–методическое пособие
для студентов факультета математики и информатики
Вариант1
1. Внутри отрезка MN случайным образом выбирается точка Х. Найдите вероятность того, что точка Х ближе к точке N, чем к M.
2. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найдите вероятность того, что при аварии сработает только один сигнализатор.
3. Из урны, содержащей 2 белых и 6 черных шаров, наудачу выбирается с возвращением 5 раз подряд один шар. Найдите вероятность того, что 4 раза появится белый шар.
4. На заводе, изготовляющем металлические линейки, первая машина производит 22%, вторая-43%, третья-35% всех изделий. В их продукции брак составляет соответственно 3:2:4. Случайно выбранное изделие оказалось дефектным. Какова вероятность того, что линейка была произведена первой машиной?
5. Среди шариковых авторучек, в среднем, при упаковке, отгрузке и доставке в магазин повреждаются 0,02%. Найдите вероятность того, что среди 5000 авторучек не более трех окажутся поврежденными.
6. В денежной лотерее выпущено 1000 билетов. Разыгрывается один выигрыш в 1000 руб., четыре – по 500 руб., пять – по 400 руб. и десять выигрышей по 100 руб. Найдите ряд распределения стоимости выигрыша для владельца одного лотерейного билета.
7. Найдите математическое ожидание дискретной случайной величины Х, распределенной по закону Пуассона.
8. Плотность вероятности случайной величины  имеет вид:
имеет вид: 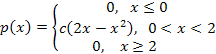
Найдите: 1) значение с; 2) функцию распределения; 3) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану.
9. Случайная величина 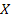 распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найдите вероятность того, что
распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найдите вероятность того, что 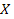 примет значение, принадлежащее интервалу (10,50).
примет значение, принадлежащее интервалу (10,50).
10. При стрельбе по мишени, представляющей собой круг радиуса 30 см, средняя величина отклонения от центра мишени равна 6 см. Пользуясь неравенством Чебышева, оцените вероятность поражения мишени при одном выстреле.
Вариант 2
1. На окружности даны точки А и В, причем эти точки не являются диаметрально противоположными. На этой же окружности выбирается точка С. Найти вероятность того, что отрезок ВС пересечет диаметр окружности, проходящий через точку А.
2. Каждый день акции корпорации поднимаются в цене или падают в цене на один пункт с вероятностями соответственно 0,75 и 0,25. Найти вероятность того, что акции после шести дней вернутся к своей первоначальной цене. Принять условие, что изменения цены акции вверх и вниз – независимые события.
3. Компьютер состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
4. В результате подбрасывания двух игральных костей на верхних гранях появляются некоторые числа. Составьте ряд распределения суммы выпавших очков.
5. Случайная величина Х задана рядом распределения
| Xi | -2 | ||
| Pi | 0,5 | 0,3 | 0,2 |
| y | -2 | ||
| P | 0,35 | 0,42 | 0,23 |
Найдите закон распределения случайных величин:
а) Y=3X; в) H=X+Y
6. Плотность распределения непрерывной случайной величины имеет вид:
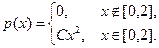
Определите: 1) константу C, 2) найдите функцию распределения F(x) и посторойте ее график; 3) вычислите вероятность 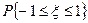 .
.
7. Случайная величина задана функцией распределения. Найдите числовые характеристики случайной величины X: M(X), D(X), 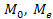

8. Событие, состоящее из мгновенного сигнала должно произойти между одним и пятью часами. Время ожидания сигнала есть случайная величина Х, имеющая равномерное распределение. Какова вероятность того, что сигнал будет зафиксирован в течение 20 мин после двух часов?
9. Случайная величина 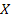 распределена нормально. Математическое ожидание и среднее квадратическое отклонение
распределена нормально. Математическое ожидание и среднее квадратическое отклонение 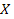 соответственно равны 20 и 10. Найдите вероятность того, что отклонение по абсолютной величине будет меньше трёх.
соответственно равны 20 и 10. Найдите вероятность того, что отклонение по абсолютной величине будет меньше трёх.
10. Изготовлена партия деталей. Среднее значение длины детали равно 50 см, а среднее квадратическое отклонение равно 0,2 см. Оцените снизу вероятность того, что длина наудачу взятой детали окажется не менее 49,5 см и не более 50,5 см.
Вариант 3
1. В круг радиуса R наудачу брошена точка. Найдите вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника.
2.. В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найдите вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.
3. Группа студентов состоит из 5 отличников, 12 хорошо успевающих и 4 занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найдите вероятность того, что он получит хорошую или отличную оценку.
4. Вероятность выигрыша приза на новогоднем вечере в университете АлтГПА по одному входному билету р=0,01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью Р, не меньшей, чем 0,98?
5. Три стрелка сделали по одному выстрелу в мишень. Вероятности попадания равны 0,6; 0,7; 0,8 соответственно. Составьте ряд распределения числа попаданий в мишень. Найдите математическое ожидание и дисперсию этой величины.
6. Дискретные случайные величины заданы рядами распределения:
| xi | -2 | ||
| P | 0,35 | 0,42 | 0,23 |
| y | -2 | ||
| Pi | 0,5 | 0,3 | 0,2 |
Составьте ряд распределения случайных величин 1) Y=X2; 2) В=Х-Y.
7. Дискретная случайная величина X имеет следующий ряд распределения вероятностей. Найдите интегральную функцию распределения и постройте ее график.
| Xi | |||||
| Pi | 0,1 | 0,15 | 0,2 | 0,35 | 0,2 |
8. Случайная величина X задана функцией плотности вероятностей
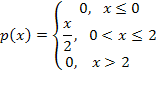 Найдите функцию распределения случайной величины X, постройте ее график. Вычислите для X ее математическое ожидание, дисперсию, моду и медиану.
Найдите функцию распределения случайной величины X, постройте ее график. Вычислите для X ее математическое ожидание, дисперсию, моду и медиану.
9. Случайная величина равномерно распределена на [a, b]. Дано ее математическое ожидание равно 1 и дисперсия равна 3. Найдите вероятность попадания случайной величины в отрезок [-3, 2].
10. Дисперсия каждой из 1000 независимых случайных величин равна 4. Оцените вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий по абсолютной величине не превысит 0,2.
Вариант 4
1. Из отрезка [0, 2] на удачу выбраны два числа х и у. Найдите вероятность того, что эти числа удовлетворяют неравенствам х²≤4у≤4х.
2. Три электрических лампочки последовательно включены в цепь. Вероятность того, что одна любая лампочка перегорит, если напряжение в цепи превысит номинальное, равна 0,6. Найдите вероятность того, что при повышенном напряжении тока в цепи не будет.
3. Определите вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
4. Имеются две урны: в первой 5 белых шаров и 7 черных; во второй 4 белых и 6 черных. Из первой урны во вторую перекладывают, не глядя, один шар. После этого - из второй урны берут один шар. Найдите вероятность того, что этот шар будет белым.
5. В связке из 3 ключей только один ключ подходит к двери. Ключи перебирают до тех пор, пока не найдется подходящий ключ. Постройте ряд распределения случайной величины X – числа перепробованных ключей. Постройте полигон распределения.
6. Даны ряды распределения двух независимых случайных величин:
| xi | |||
| pi | 0,5 | 0,2 | 0,3 |
| yj | -2 | ||
| pj | 0,1 | 0,6 | 0,2 |
Найдите ряд распределения случайной величины Z=X-Y, ее дисперсию.
7. Случайная величина Х задана функцией распределения F(x):
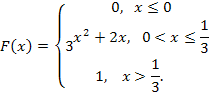
Найдите: а) плотность распределения вероятностей, б) математическое ожидание, дисперсию, среднее квадратичное отклонение, медиану и моду случайной величины Х; в) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу (1/6; 1/3).
8. Найдите функцию распределения случайной величины Х, распределенной равномерно на отрезке [a,b].(вывести формулу)
9. На станке изготавливается некоторая деталь. Ее длина Х - случайная величина, распределенная по нормальному закону со средним значением 20 см и дисперсией 0,2. Найдите вероятность того, что длина детали отклонится от средней длины менее, чем на 0,3?
10. Автомат изготавливает шарики. Шарик считается годным, оклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина распределена нормально с параметрами а=0 и  . Найдите сколько, в среднем, будет годных шариков среди 100 изготовленных.
. Найдите сколько, в среднем, будет годных шариков среди 100 изготовленных.
Вариант 5
1. В коробке лежат 5 синих, 4 красных, 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Найдите вероятность того, что это будут карандаши разного цвета.
2. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найдите вероятность того, что в цель попали не менее трех раз.
3. Известно, что в среднем, 95% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98, если она стандартна, и с вероятностью 0,06, если она не стандартна. Какова вероятность того, что взятое наудачу изделие пройдет упрощенный контроль.
4. Учитель проверяет в среднем за четверть 500 тетрадей. Вероятность того, что он допустит ошибку при проверке тетради, равна 0,008. Определите вероятность того, что учитель допустит ошибку при проверке 5 тетрадей.
5. Три пассажира наугад рассаживаются в двух вагонах. Найдите ряд распределения числа пассажиров, севших в первый вагон. Вычислите математическое ожидание и дисперсию этой случайной величины.
6. Найдите математическое ожидание случайной величины Z = 4X-2Y, если известны математические ожидания M(X) = 5, M(Y) = 3.
7. Задана непрерывная случайная величина Х функцией распределения F(Х). Найдите:
1) плотность распределения вероятностей f(x), постройте ее график;
2) математическое ожидание, дисперсию и среднее квадратическое отклонение, моду и медиану непрерывной случайной величины Х.
3) вероятность того, что Х примет значение из интервала (- 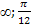 )
)
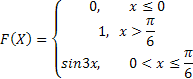
8. Найдите дисперсию случайной величины Х, равномерно распределенной в интервале (a,b).(вывести формулу)
9. Полагая, что рост мужчин определённой возрастной группы есть нормально распределённая случайная величина 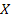 с параметрами
с параметрами 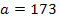 и
и 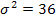 . Найдите
. Найдите
функцию плотности вероятности и функцию распределения случайной величины 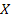 .
.
10. Оцените вероятность того, что в результате подбрасывания игральной кости в течении 320 раз относительная частота появления на верхней грани пяти очков отклонится от вероятности этого события (по абсолютной величине) не более чем на 0,03.
Вариант 6
1. На шахматную доску с шириной клетки 5 см брошена монета радиуса 1,5 см. Найдите вероятность того, что монета не попадет ни на одну границу.
2. На кафедре работают 12 преподавателей. При существующем расписании вероятность, что преподаватель в данный момент на занятии, равна 0,8. Какова вероятность того, что в данный момент не менее 10 преподавателей заняты на парах.
3. В некоторой отрасли 30% продукции производится фабрикой 1-ой, 25% продукции – фабрикой 2-ой, а остальная часть продукции – фабрикой 3-ей. На фабрике 1 в брак идет 1% всей производимой ею продукции, на фабрике 2 – 1,5%, на фабрике 3 – 2%. Купленная покупателем единица продукции оказалась браком. Какова вероятность того, что она произведена фабрикой 1?
4. В сельской школе учатся 100 учеников, которые учатся независимо друг от друга. Вероятность получения двойки любым из учеников в течение времени T равна 0,02. Найти вероятность того, что за время Т получат двойки ровно 7 учеников. 0,003
5. Контрольная работа состоит из четырех вопросов. На каждый вопрос дано по 5 ответов, среди которых имеется один правильный. Составьте ряд распределения вероятностей случайного числа X правильных ответов, полученных при простом угадывании, и найдите интегральную функцию распределения вероятностей этой случайной величины.
6. Даны законы распределения двух независимых случайных величин:
| xi | -1 | ||
| pi | 0,4 | 0,24 | 0,36 |
| yj | -3 | ||
| pj | 0,01 | 0,8 | 0,19 |
Найдите ряд распределения случайной величины Z=XY
7. Плотность распределения непрерывной случайной величины X имеет вид:
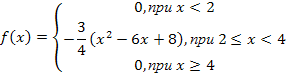
Найдите математическое ожидание, дисперсию, среднее квадратичное отклонение, моду и медиану.
8. Цена деления шкалы амперметра равна 0,1 А. Показания амперметра округляют до ближайшего целого деления. Найдите вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.
9. Пусть случайная величина 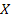 распределена по нормальному закону с плотностью 4. Найдите вероятность попадания величины
распределена по нормальному закону с плотностью 4. Найдите вероятность попадания величины 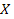 в произвольный отрезок
в произвольный отрезок 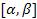 .(вывести формулу)
.(вывести формулу)
10. Устройство состоит из 100 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,03. Оцените вероятность того, что абсолютная величина разности между средним числом отказов (математическим ожиданием) и числом отказов за время Т окажется меньше двух.
Вариант 7
1. Набирая номер телефона, абонент забыл последние 3 цифры и, помня лишь, что эти цифры различны, набрал их на удачу. Найдите вероятность того, что набраны нужные цифры.
2. Из колоды в 36 карт вынимаются одна за другой без возвращения 6 карт. Какова вероятность того, что три них будут «черви»?
3. Вероятность сдать экзамен для каждого из 6 студентов равна 0,8. Найдите вероятность того, что сдадут экзамен пять студентов.
4. Прибор выходит из строя при отказе (неисправности) его микросхемы. Вероятность отказа в течение 1 ч работы прибора 0,02. С какой вероятностью за 100 ч эксплуатации прибора микросхему придется менять три раза?
5. Из 800 учебников хранящихся в библиотеке вероятность того, что книга испорчена, составляет 0,5%. Чему равна вероятность того, что испорчено ровно 6 учебников?
6. Дан ряд распределения случайной величины X:
| Xi | -2 | -1 | |||
| Pi | 0,1 | 0,2 | 0,2 | 0,4 | 0,1 |
Требуется: а) построить многоугольник распределения; б) построить функцию распределения F(x) и начертить ее график; в) найти вероятность того, что величина X примет значение, непревосходящее по абсолютной величине 1.
7. Составьте ряд распределения дискретной случайной величины Х, принимающей значения х1=1, х2=3, х3=4, если известно, что М(Х)=2,3, а D(X)=1,21.
8. Найдите вероятность того, что в результате испытания случайная величина примет значение в интервале (-2;2). Вычислите математическое ожидание, дисперсию и среднее квадратичное отклонение, моду, медиану непрерывной случайной величины:
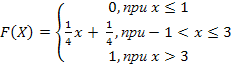 (
(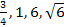 )
)
9. Поезда метрополитена идут регулярно с интервалом 2 мин. Какова вероятность того, что ждать пассажиру придется не больше полминуты. Найдите математическое ожидание и среднее квадратичное отклонение случайной величины Х – время ожидания поезда.
10. Производится измерение диаметра вала без симметрических (одного значения) ошибок. Случайные ошибки измерения 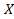 подчинены нормальному закону со средним квадратическим отклонением
подчинены нормальному закону со средним квадратическим отклонением 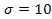 мм. Найдите вероятность того, что измерение будет произведено с ошибкой, непревосходящей по абсолютной величине 15 мм. 0,866 4
мм. Найдите вероятность того, что измерение будет произведено с ошибкой, непревосходящей по абсолютной величине 15 мм. 0,866 4
Вариант 8
1. В секретном замке на общей оси 4 диска, каждый из которых разделен на 5 секторов, на которых написаны различные цифры. Замок открывается, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найдите вероятность того, что при произвольной установке дисков замок будет открыт.
2. В мешке смешаны нити трех цветов: 30% белых, 50% красных, остальные зеленые. Определите вероятность того, что при последовательном вытягивании наугад трех нитей окажется, что все они одного цвета.
3. Имеются три одинаковых по виду ящика. В первом 20 белых шаров, во втором – 10 белых и 10 черных шаров, в третьем – 20 черных шаров. Из выбранного наугад ящика вынули белый шар. Вычислите вероятность того, что шар вынут из первого ящика.
4. Вероятность того что студент не получит зачет по физкультуре равна 0,05. Какова вероятность того, что из 100 студентов зачет не получит 20 студентов?
5. Составьте ряд распределения числа мальчиков в семье из 3 детей. Вероятность рождения мальчика равна 0,515. Постройте многоугольник распределения.
6. Даны законы распределения двух независимых случайных величин:
| xi | -1 | ||
| pi | 0,4 | 0,24 | 0,36 |
| yj | -3 | ||
| pj | 0,01 | 0,8 | 0,19 |
Найдите ряд распределения случайной величины Z=X-Y, ее дисперсию.
7. Функция распределения задана следующим выражением:
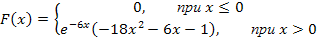
Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение, моду и медиану Х.
8. Найдите математическое ожидание случайной величины Х, имеющей нормальное распределение. (вывести формулу)
9. Срок службы прибора представляет собой случайную величину, подчинённую нормальному закону распределения, с гарантией на 15 лет и средним квадратическим отклонением равным 3 года. Определите вероятность того, что прибор прослужит от 10 до 20 лет.
10. Средний расход воды на животноводческой ферме составляет 1000 л. в день, а среднее квадратичное отклонение этой случайной величины не превышает 200 л. Оцените вероятность того, что расход воды на ферме в любой выбранный день не превзойдет 2000 л, используя неравенство Чебышева.
Вариант 9
1. Набирая номер телефона, абонент забыл последние 3 цифры и, помня лишь, что эти цифры различны, набрал их на удачу. Найдите вероятность того, что набраны нужные цифры.
2. В ящике находится 20 деталей. Известно, что 5 из них являются стандартными. Из этих деталей выбирают 3. Сколько существует способов выбора трех деталей таких, чтобы среди них была, по крайней мере, одна стандартная?
3. Ведется доказательство двух теорем. Каждая из теорем, независимо от другой, может быть доказана в течение суток с вероятностью 0,5. После доказательства одной из теорем, в связи с увеличением количества студентов, занятых в доказательстве, вероятность доказать вторую теорему возрастает до 0,7. Какова вероятность того, что в течение суток будут доказаны обе теоремы.
4. Небольшой город ежедневно посещают 100 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы c вероятностью приблизительно 0,99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно для этого быть в его ресторане?
5. Найдите вероятность того, что среди 200 учеников школы №42 окажется 4 левшей, если, в среднем, левши составляют 1%.
6. В стопке из 6 тетрадей имеется четыре с оценкой отлично. Наудачу отобраны три тетради. Составьте ряд распределения числа работ с оценкой «отлично», оказавшихся в выборке. Найдите дисперсию.
7. Функция плотности вероятности 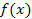 задана в виде:
задана в виде:
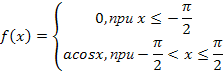
Найдите: а) значение постоянной А, при которой функция будет плотностью вероятности некоторой случайной величины Х; б) вероятность попадания в интервал 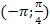 , в) моду и медиану.
, в) моду и медиану.
8. Найдите вероятность попадания равномерно распределенной на (а, b) случайной величины Х в промежуток [ 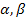 ]
] 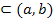 .(вывести формулу)
.(вывести формулу)
9. Распределение веса консервных банок, выпускаемых заводом, подчиняется закону нормального распределения со средним весом 250 г. и средним квадратическим отклонением равным 5 г. Определите вероятность того, что отклонение веса банок от среднего веса по абсолютной величине не превысит 8 г. 0,8904
10. Пусть случайная величина Х имеет D(X)=0,001. Какова вероятность того, что она отличается от M(X) более чем на 0,1? 0,1
Вариант 10
1. В почтовом отделении имеются открытки 6 видов. Какова вероятность того, что среди 4 проданных открыток все открытки различны?
2. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность того, что оба шара окажутся белыми?
3. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе - 0,9, в третье - 0,8. Найдите вероятность того, что хотя бы одно отделение получит газеты с опозданием.
4. Три экзаменатора принимают экзамен по некоторой дисциплине у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студента, а третий — 21 студентов (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Найдите вероятность того, что слабо подготовившийся студент сдаст экзамен.
5. Вероятность того, что студент опоздает на пару, равна 0,01. Какова вероятность того, что из 1000 студентов опоздает ровно 4 студента.
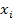
| ||||
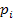
| 0,4 | 0,1 | 0,3 | 0,2 |
6. Дан ряд распределения случайной величины X. Найдите ее функцию распределения, постройте график.
7. Функция 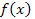 задана в виде:
задана в виде: 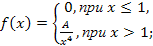
Найдите: а) значение постоянной А; б) выражение функции распределения F(х); в) вероятность того, что случайная величина Х примет значение на отрезке [2;3]; г) математическое ожидание, дисперсию, моду и медиану случайной величины Х.
8. Найдите дисперсию случайной величины, имеющей равномерное распределение на [a, b]. (вывести формулу)
9. Исследуйте функцию плотности вероятности случайной величины, имеющей нормальное распределение. Постройте ее график.(с помощью производной).
10. Систематическая ошибка высотомера равна нулю, а случайные ошибки распределены по нормальному закону. Какую среднеквадратическую ошибку должен иметь высотомер, чтобы с вероятностью 0,9 ошибка измерения высоты по абсолютной величине была меньше 100 метров?
Вариант 11
1. В денежно-вещевой лотерее из 1000 билетов на 24 выдают денежные выигрыши и на 10 вещевые. Вы приобрели 2 билета. Какова вероятность выигрыша хотя бы по 1 билету?
2. В аудитории стоят компьютеры трех заводов, причем доля компьютеров первого завода - 60%, второго- 25%, а остальная часть продукции – доля компьютеров третьего завода. Брак их продукции составляет соответственно 1%, 1,5%, 2%. Купленная покупателем единица продукции оказалась бракованной. Какова вероятность того, что она произведена первым заводом?
3. Производится залп из шести орудий по некоторому объекту. Вероятность попадания в объект из каждого орудия равна 0,6. Найдите вероятность ликвидации объекта, если для этого необходимо не менее четырех попаданий.
4. Найдите вероятность того, что при 3600 независимых бросаниях игральной кости число появлений 6 очков будет не меньше 900.
5. Страховая компания заключила 40000 договоров. Вероятность страхового случая по каждому из них в течение года составляет 2%. Найдите вероятность, что таких случаев будет не более 870.
6. Вероятность поражения вирусным заболеванием куста земляники равна 0,2. Составьте закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов. Вычислите основные числовые характеристики.
7. Непрерывная случайная величина задана интегральной функцией F(x). F(x)= 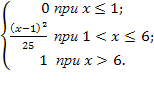
Найдите: а) вероятность попадания случайной величины в интервал (2;4);
б) дифференциальную функцию распределения; в) M(x), D(x), 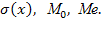
8. В продукции цеха детали отличного качества составляют 50%. Детали укладываются в коробки по 200 шт. в каждой. Какова вероятность того, что число деталей отличного качества в коробке отличаться от 100 не более, чем на 5?
- Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 10 и 2. Найдите вероятность того, что в результате испытания X примет значение, заключенное в интервале (12, 14).
10. Вероятность наступления события А в каждом из 1000 независимых опытов равна 0,8. Найдите вероятность того, что число наступлений события А в этих 1000 опытах отклонится от своего математического ожидания по абсолютной величине меньше чем на 50. 0,963
Вариант 12
1. Для поражения цели необходимо попасть в нее дважды. Вероятность первого попадания равна 0,2, затем она не меняется при промахах, но после первого попадания увеличивается вдвое. Найти вероятность того, что цель будет поражена первыми двумя выстрелами. 0,08
2. Группа студентов состоит из 5 отличников, 12 хорошо успевающих и 4 занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найдите вероятность того, что он получит хорошую или отличную оценку.
3. В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найдите вероятности событий:
В – наудачу взятая коробка содержит 13 бракованных изделий;
С – число бракованных изделий в коробке не превосходит 20.
4. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определите наивероятнейшее число попаданий в цель и вероятность этого события.
5. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают 1 шар и возвращают назад и перемешивают.Приняв за случайную величину Х число извлеченных белых шаров, составьте ряд распределения Х, найдите М(Х)и D(X).
6. Непрерывная случайная величина задана интегральной функцией F(x). Найдите а) вероятность попадания случайной величины в интервал(1;2); б) дифференциальную функцию f(x); в) M(x), D(x), 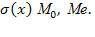 F(x)=
F(x)= 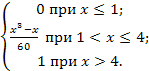
7. Автомат изготовляет шарики. Шарик считается годным, если отклонение X диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением а = 0,4 мм. Найдите, сколько в среднем, будет годных шариков среди ста изготовленных.
8. Телефонная станция обслуживает 2000 абонентов, в час пик каждый абонент использует связь в среднем в течение 2 минут, т.е. мы считаем, что абонент с вероятностью  использует связь. Какое наименьшее число линий необходимо, чтобы только один из 100 вызовов получал отказ? 86 линий
использует связь. Какое наименьшее число линий необходимо, чтобы только один из 100 вызовов получал отказ? 86 линий
9. Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найдите вероятность того, что длина наудачу взятой детали больше 55 мм.
10. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 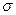 = 20 мм и математическим ожиданием а = 0. Найдите вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.
= 20 мм и математическим ожиданием а = 0. Найдите вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.
Вариант 13
1. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найдите вероятность того, что откажут не менее четырех элементов.
2. Для приема зачета преподаватель приготовил 50 задач: 20 задач по дифференциальному и 30 задач по интегральному исчислению. Для получения зачета студент должен решить первую попавшуюся ему задачу. Какова вероятность для студента получить зачет, если он знает решение 18 задач по дифференциальному и 15 по интегральному исчислению?
3. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найдите вероятность того, что случайно купленная новая продукция окажется высшего сорта.
4. Вероятность рождения мальчика в регионе составляет р = 0.51. Какова вероятность того, что из 500 новорожденных в регионе мальчиков не менее 250?
- Тест по теории вероятностей состоит из 10 вопросов. На каждый вопрос в тесте предлагается 4 варианта ответа, из которых надо выбрать один правильный. Какова вероятность того, что, совершенно не готовясь к тесту, студенту удастся угадать правильные ответы по крайней мере на 6 вопросов?
6. Три стрелка делают по одному выстрелу в мишень. Вероятности попадания равны 0,6; 0,7; 0,8 соответственно. Составьте ряд распределения числа попаданий в мишень. Найдите математическое ожидание и дисперсию.
7. Найдите математическое ожидание, дисперсию, медиану и моду непрерывной случайной величины Х, заданной плотностью распределения.
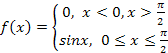
8. Устройство состоит из 100 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,03. Оцените вероятность того, что абсолютная величина разности между числом (математическим ожиданием) отказов за время Т окажется не меньше двух.
9. Случайная величина 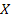 распределена нормально. Математическое ожидание и среднее квадратическое отклонение
распределена нормально. Математическое ожидание и среднее квадратическое отклонение 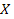 соответственно равны 20 и 10. Найдите вероятность того, что отклонение по абсолютной величине будет меньше трёх.
соответственно равны 20 и 10. Найдите вероятность того, что отклонение по абсолютной величине будет меньше трёх.
10. Изготовлена партия деталей. Среднее значение длины детали равно 50 см, а среднее квадратическое отклонение равно 0,2 см. Оцените снизу вероятность того, что длина наудачу взятой детали окажется не менее 49,5 см и не более 50,5 см
Вариант 14
1. Найдите вероятность попадания в паутину бабочки оказавшейся в колодце различной формы?

2. Имеются две урны: в первой 5 белых шаров и 7 черных; во второй 4 белых и 6 черных. Из первой урны во вторую перекладывают, не глядя, один шар. После этого из второй урны берут один шар. Найдите вероятность того, что этот шар будет белым.
3. Проверкой установлено, что 96% изделий служат не меньше гарантируемого срока. Наугад выбирают 15000 изделий. Найдите вероятность того, что со сроком службы менее гарантируемого будет от 570 до 630 изделий.
4. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найдите вероятность того, что откажут:
а) три элемента; б) не менее четырех элементов; в) хотя бы один элемент.
5. Три экзаменатора принимают экзамен по некоторой дисциплине у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студента, а третий — 21 студентов (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Известно, что студент сдавал экзамен, но получил «неудовлетворительно». Кому из трех преподавателей вероятнее всего он отвечал?
6. Составьте ряд распределения числа девочек в семье их четырех детей, если вероятность рождения мальчика равна 0,515. Найдите математическое ожидание и дисперсию.
7. Непрерывная случайная величина X задана функцией распределения:
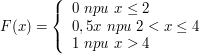
Найдите: а) вероятность того, что в результате испытания X примет значение меньшее 0,2; б) математическое ожидание, дисперсию, медиану и моду непрерывной случайной величины Х
8. Выведите формулу для дисперсии случайной непрерывной величины, имеющей нормальное распределение.
9. Проведённое исследование показало, что вклады населения в данном банке могут быть описаны случайной величиной 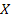 , распределённой по нормальному закону с параметрами
, распределённой по нормальному закону с параметрами 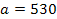 ,
, 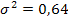 . Найдите средний размер вклада.
. Найдите средний размер вклада.
10. Дисперсия каждой из 1000 независимых случайных величин xk (k = 1, 2,..., 1000) равна 4. Оцените вероятность того, что отклонение средней арифметической этих величин от средней арифметической их математических ожиданий по абсолютной величине не превзойдет 0,1.
Вариант 15
1. Студент знает 20 из 25 вопросов программы. Зачёт сдан, если студент ответит не менее чем на 3 из 4-х вопросов в билете. Взглянув на первый вопрос, студент обнаружил, что знает его. Какова вероятность, что студент сдаст зачёт?
2. Известно, что в среднем 95% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98, если она стандартна, и с вероятностью 0,06, если она не стандартна. Определите вероятность того, что взятое наудачу изделие пройдет упрощенный контроль.
3. Вероятность наступления события А в каждом из одинаковых и независимых испытаний равна 0,7. Найдите вероятность того, что в 1600 испытаниях событие А наступит ровно 1100 раз.
4. В магазин поступили шариковые ручки одного типа, изготовленные на четырех заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что ручка пропишет более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина ручки были перемешаны. Какова вероятность того, что купленная ручка пропишет более 1500 часов?
5. Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5?
- Школьник при подготовке к ГИА по математике использует сборник 2011 года, который может купить в четырех книжных магазинах города. Составьте ряд распределения числа посещенных магазинов для приобретения нужного источника, если вероятность того, что книга имеется в продаже 0,3. Вычислите математическое ожидание и дисперсию.
7. Непрерывная случайная величина X задана интегральной функцией:
F(x)= 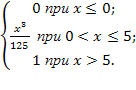 Постройте график этой функции. Определите: a) вероятность попадания случайной величины в интервал (2;3); б) математическое ожидание, дисперсию, медиану и моду непрерывной случайной величины Х.
Постройте график этой функции. Определите: a) вероятность попадания случайной величины в интервал (2;3); б) математическое ожидание, дисперсию, медиану и моду непрерывной случайной величины Х.
8. Случайная величина 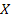 распределена нормально. Математическое ожидание и среднее квадратическое отклонение
распределена нормально. Математическое ожидание и среднее квадратическое отклонение 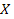 соответственно равны 20 и 10. Найдите вероятность того, что отклонение по абсолютной величине будет меньше трёх.
соответственно равны 20 и 10. Найдите вероятность того, что отклонение по абсолютной величине будет меньше трёх.
9. Изготовлена партия деталей. Среднее значение длины детали равно 50 см, а среднее квадратическое отклонение равно 0,2 см. Оцените снизу вероятность того, что длина наудачу взятой детали окажется не менее 49,5 см и не более 50,5 см.
10. Оцените вероятность того, что в результате подбрасывания игральной кости в течении 320 раз относительная частота появления на верхней грани пяти очков отклонится от вероятности этого события (по абсолютной величине) не более чем на 0,03.
Вариант 16
1. На отрезок [0, 4] случайно бросаются две точки. Найдите вероятность того, что одна из них находится от левого конца отрезка на расстоянии меньшем 2, а другая от правого конца отрезка на расстоянии меньшем 1. Сделать чертеж.
2. В урне 10 белых и 6 черных шаров. Наудачу извлекается 4 шара. Определите вероятность того, что а) все шары белого цвета; б) 1 шар белый, а остальные черные; в) все шары одного цвета.
3. Вступительные экзамены на специальность «менеджмент» сдают 200 абитуриентов, а на специальность «финансы и кредит» - 300 абитуриентов. Вероятность успешной сдачи экзаменов на «менеджмент» равна 0,6, а на «финансы и кредит» - 0,7.
а) Какова вероятность, того что наудачу выбранный абитуриент успешно сдал экзамены.
б) Наудачу выбранный абитуриент успешно сдал экзамены. Какова вероятность того, что он со специальности «финансы и кредит».
4. Вероятность того, что год урожайный равна 0,7. Какова вероятность того, что из пяти рассматриваемых лет менее трех лет будут неурожайными?
5. В результате многолетних наблюдений установлено, что вероятность выпадения дождя 1 сентября в данном городе равна  . Определите наивероятнейшее число дождливых дней 1 сентября в данном городе за 40 лет. Найдите вероятность этого события.
. Определите наивероятнейшее число дождливых дней 1 сентября в данном городе за 40 лет. Найдите вероятность этого события.
6. В лотерее на каждые 100 билетов приходится 1билет с вы-игрышем 20тыс. рублей, 2билета с выигрышем 10тыс. рублей, 8билетов с выигрышем 5тыс. рублей и т.д. Остальные билеты из сот-ни не выигрывают. Составьте закон распределения величины выигрыша для вла-дельца одного билета и найти его основные характеристики: матема-тическое ожидание, дисперсию и среднее квадратическое отклоне-ние. Поясните смысл указанных характеристик.
7. Дана плотность распределения вероятностей непрерывной случайной величины 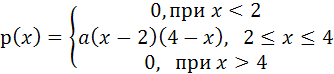
Определите значение параметра a, математическое ожидание, дисперсию, моду и медиану распределения.
8. Найдите среднее квадратическое отклонение случайной величины, имеющей равномерное распределение. (вывести формулу).
9. Мастерская изготавливает стержни, длина которых L представляет собой случайную величину, распределенную по нормальному закону с математическим ожиданием 25 см и средним квадратическим отклонением 0,1 см. Определите вероятность того, что отклонение длины стержня от математического ожидания по абсолютной величине, не превзойдет 0,25 см.
10. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 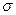 = 20 мм и математическим ожиданием а = 0. Найти вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм. 0,57809
= 20 мм и математическим ожиданием а = 0. Найти вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм. 0,57809
Поиск по сайту: