Система предпочтительных чисел и требования, предъявляемые к рядам предпочтительных чисел

Предпочтительные числа и ряды предпочтительных чисел являются основанием для выбора величин и градаций параметров всех видов про­дукции, что позволяет наилучшим образом согласовать и увязать между собой изделия, полуфабрикаты, материалы, транспортные средства, тех­нологическое, контрольно-измерительное и другое оборудование.

Использование предпочтительных чисел при конструировании обеспечивает предпосылки для обеспечения взаимозаменяемости деталей и сборочных единиц, для унификации конструкций машин.

Ряды предпочтительных чисел удовлетворяют следующим требо­ваниям:

1. предоставляют рациональную систему градаций, которая отвечает потребности производства и эксплуатации

2. являются неограни­ченными как в направлении уменьшения, так и в направлений увели­чения чисел, т. е. допускают неограниченное развитие параметров или размеров в направлении увеличения и направлении уменьшения;

3. вклю­чают все десятичные кратные или дробные значения любого числа, а также единицу; являются простыми и легко запоминаются.

Перечисленными свойствами обладают числа, которые являют­ся геометрическими прогрессиями.

Ряды таких чисел включают це­лые степени десяти и имеют знаменатели прогрессии, равные

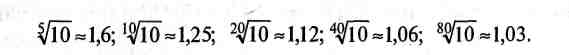
Основные, производные, ограниченные и составные ряды. Установ­лено четыре основных десятичных ряда предпочтительных чисел:

R5--φ= 1,6 (1,00; 1,60; 2,50; 4,00; 6,30; 10;...);

R10--φ= 1,25 (1,00; 1,25; 1,60; 2,00; 2,25;...);

R20--φ= 1,12 (1,00; 1,12; 1,25; 1,40;...);

К40--φ = 1,06 (1,00; 1,06; 1,12; 1,18; 1,25;...).

Каждый член ряда получают путем умножения предыдущего члена на знаменатель прогрессии φ

В некоторых технически обоснованных случаях допускается исполь­зование дополнительного ряда предпочтительных чисел R80 — φ= 1,03.

Номер ряда предпочтительных чисел R5, R10, R20, R40, R80 указывает на количество чисел в десятичном интервале (интервал, в котором числа ряда увеличиваются в десять раз). Так, ряд R10 содержит в десятичном интервале 10 чисел.

Например, ряд R5 составляют числа с номерами 0-8-16-24-32-40; ряд R10 числа: 0-4-8-12-16-20-24-28-32-36-40 и т. д.

В ряды предпочтительных чисел входит округленное значение чис­ла «Пи» число 3,15 (номер 20 в табл.). Число Пи(отношение длинны окружности к диаметру), выражается бесконечной непериодической десятичной дробью:П = 3,141 592 653 589 793 238 462 643...

14 марта - Всемирный день числа ПИ. По давней традиции, именно в этот день каждый год проходит торжественная конференция, посвященная проблеме числа ПИ в математике.

Предпочтительные числа ряда R40