Регулярный режим охлаждения (нагрева). Теоремы Кондратьева. В нестационарном процессе охлаждения (нагрева) как однородных, так и неоднородных тел любой формы и размеров в жидкой сре­де с постоянной температурой Тж

В нестационарном процессе охлаждения (нагрева) как однородных, так и неоднородных тел любой формы и размеров в жидкой сре­де с постоянной температурой Т_ж можно вы­делить три характерных режима:

1) неупорядоченный (0 < τ < τ_р) — начальное распределение температур оказы­вает заметное влияние на развитие процесса. Температурное поле одномерных тел на этой стадии описывается рядом:

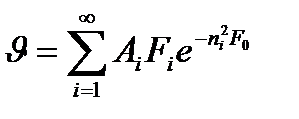, (10.1)

где A_i – постоянные коэффициенты, зависящие от заданных начальных условий и не зависящие ни от координат, ни от времени; F_i – функция, зависящая от координат и начальных условий.

2) регулярный (τ_р < τ < ∞) — при котором поле избыточной температуры θ автомодельно по времени, т.е. остается подобным при изменении времени. Характерен тем, что влияние начального распределения температур исчезает. Для описания поля температур достаточно первого члена ряда (10.1).

3) стационарный (τ → ∞) – температура во всех точках тела становится равной температуре окружающей жидкости Т_ж.

В стадии регулярного режима относительная скорость изменения избыточной температуры 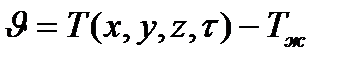в любой точке тела остается постоянной и одинаковой:

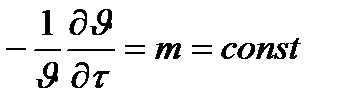. (10.2)

Эта скорость, имеющая размерность 1/с, называется темпом охлаждения (нагрева). Величина m зависит от физических свойств тела, его формы и размеров, коэффициента теплопередачи α.

В регулярном режиме изменение во времени носит линейный характер (рис. 10.1).

Это позволяет легко обнаружить в эксперименте наступление регулярного режима и, фиксируя температуру в произвольной точке тела для двух моментов времени τ₁ и τ₂ рассчитать темп охлаждения:

Теория регулярного режима разработана Г.М. Кондратьевым. Ее основное содержание составляют две теоремы.

Рис. 10.1 – Изменение во времени температуры

тела при его охлаждении

Первая теорема Кондратьева. Согласно этой теореме для однородных тел при конечном значении α выполняется соотношение:

, (10.3)

где с, ρ – удельная теплоемкость и плотность материала тела; F, V – площадь поверхности и объем тела; - коэффициент неравномерности температурного поля, равный отношению средней по поверхности избыточной температуры к средней по объему .

Коэффициент ψ остается постоянным в течении всего периода регулярного режима, причем , и рассчитывается по формуле:

, (10.4)

где - модифицированная форма записи числа Био; К – коэффициент формы, который определяется формой и размерами тела.

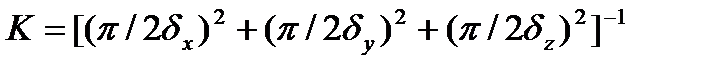- для параллелепипеда;

- для цилиндра конечной длины;

- для шара радиусом R.

Вторая теорема Кондратьева. Она уста­навливает пропорциональность между тем­пом охлаждения т и температуропровод­ностью а материала однородного тела при высокой интенсивности теплоотдачи (коэф­фициент теплоотдачи α → ∞)

т = а/К (10.5)

На основе теории регулярною режима разработаны методы экспериментального определения теплофизических свойств ве­ществ, коэффициента теплоотдачи и др.

Поиск по сайту: