Уравнение теплопроводности. Предположим, что температурное поле изменяется только в направлении х (рис

Предположим, что температурное поле изменяется только в направлении х (рис. 4.1). Пусть q₁ — плотность теплового потока в сечении х, а q₂ — в сечении x+dx,если dх мало, то в первом приближении изменение теп­лового потока в направлении оси х описывается двумя членами разложения q₁ в ряд Тейлора:

. (4.1)

Найдем разность Q₁ между входящим и выходящим количествами теплоты с единичной поверхности S = 1 за время dτ:

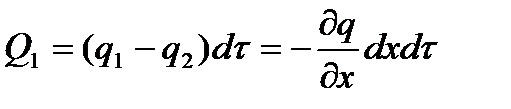. (4.2)

Сформулируем закон сохранения энергии для рассматриваемого элемента.

Количество теплоты Q₁ вместе с энергией q_vdxdτ внутренних источников расходуется на изменение температуры dt объема Adx:

, (4.3)

где q_v — объемная плотность теплового потока, Вт/м³; с_р — удель­ная теплоемкость при постоянном давлении; ρ — плотность материа­ла. Подставим в последнее уравнение значение q из формулы Фурье (); после преобразований получим уравнение теплопро­водности:

. (4.4)

Для анизотропного тела в направлении осей х, у, z теплопро­водности λ_х, λ_у, λ_я имеют различные значения и дифференциальное уравнение принимает вид:

, (4.5)

при этом тело должно быть ограничено плоскостями, перпендику­лярными осям х, у, z.

Для изотропного тела λ_х= λ_у= λ_z= λ уравнение примет вид:

, (4.6)

где a = λ/(c_pρ) – температуропроводность материала, характеризующая способность материала повышать свою температуру с большей или меньшей скоростью при аккумулировании теплоты; - оператор Лапласа. В декартовых координатах:

, (4.7)

В стационарном режиме ( =0) уравнение теплопроводности примет вид:

. (4.8)

Поиск по сайту: