Вынужденная конвекция в трубах и каналах. Гладкие трубы и каналы. В качестве определяющего размера для круглых труб принимают диаметр, а для некруглых – эквивалентный диаметр

Гладкие трубы и каналы. В качестве определяющего размера для круглых труб принимают диаметр, а для некруглых – эквивалентный диаметр, рассчитываемый по формуле:

d_эк = 4A/U. (16.1)

где А — площадь поперечного сечения канала; U — полный пери­метр сечения независимо от того, какая часть этого периметра уча­ствует в теплообмене.

Скорость определяют по формуле (15.5). При постоянной плотности q локальное число Нуссельта Nu_∞ для канала шириной h равно:

Nu_∞ = αh/λ_f = 4,12; α = q/(t_w – t), (16.2)

где t_w, t – температура стенки и средняя расходная температура жидкости на расстоянии х; λ_f – теплопроводность жидкости.

При x ≤ l_н и Pr ≈ 1 (газы) локальное число Нуссельта равно (рис. 16.1):

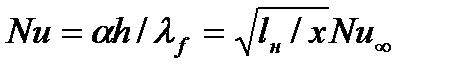. (16.3)

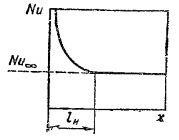На рис. 16.1 показан в соответствии с формулой (16.3) характер изменения локального числа Nu с расстоянием x от входа в канал. Для воздуха (Pr ≈ 0,7) длина l_н участка стабилизации может быть оценена по формуле:

l_н = 0,01 h Re, Re = v h/ν. (16.4)

Среднее на участке х число Нуссельта 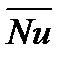для гладкого канала при ламинарном движении жидкости оценивается по формулам:

(16.5)

где l_н – длина участка стабилизации, рассчитываемая по формуле (16.4), а число Nu_∞ - по формуле (16.2).

В приведенных выше формулах предполагалось, что канал не­ограниченной длины без поворотов, поэтому явлением свободной конвекции в этом случае можно пренебречь. Однако исследования показывают, что при ламинарном движении теплообмен внутри трубы определяется факторами как вынужденного (Re), так и свободного движения (Gr). В частности, для воздуха среднее чис­ло 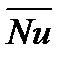по всей длине трубы:

; ,

где 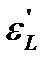- поправочный коэффициент на ограниченность трубы.

При значениях числа Рейнольдса Re>2200 ламинарный режим течения нарушается, наступает переходный режим, который при Re>10⁴ становится турбулентным. Установле­но, что коэффициент теплоотдачи при турбулентном течении мало зависит от граничных условий на поверхности стенок, но зато на теплообмен существенно влияют начальная турбулизация потока и форма входной кромки канала. Многообразие этих условий при­водит к большому числу частных эмпирических зависимостей, однако можно указать на следующую закономерность: длина l_н участка тепловой стабилизации равна примерно (15-30) d (будем полагать l_н ≈20 d). Значение среднего числа (Nu_∞)_T на стабилизи­рованном участке в турбулентном режиме течения в неограничен­ной прямой трубе диметром d:

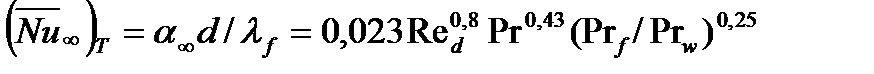, Re _d = v d/ν.

Если труба изогнута (радиус кривизны R)и ограничена, то для воды и воздуха последняя, формула может быть представлена в виде:

,

где Z – параметр, учитывающий физические свойства жидкости; ε_L – поправка на ограниченность трубы; 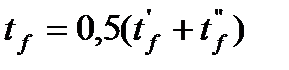- определяющая температура, равная средней между температурами входа и выхода; R – радиус кривизны изогнутой трубы.

Значения локального числа Nu_d на расстоянии х, а так­же осредненного по длине х числа при турбулентном режиме на участке нестабилизированного движения х ≤ l_н=20d:

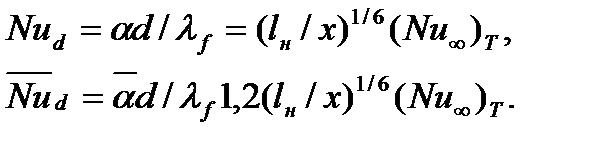(16.6)

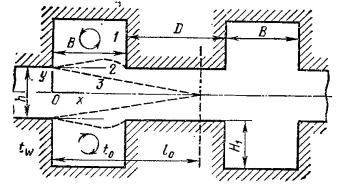Движение жидкости в каналах с впадинами и выступами. Рас­смотрим движение жидкости через каналы, имеющие впадины и выступы, соизмеримые с шириной канала. Последние могут быть образованы при монтаже на платах элементов, микромодулей, интегральных схем (ИС), больших интегральных схем (БИС) и т.д. Упрощенная схема движения жидкости через каналы с поперечными впадинами представлена на рис. 6.2. Если ширина канала h существенно меньше длины участка D, то такой участок можно представить как плоский канал с гладкими стенка­ми. На участке В движе­ние становится более сложным и можно выде­лить три зоны: зону 1 циркуляционного движе­ния во впадине, зону 3 струйного движения и промежуточную зону 2 между ними. На начальном участке х = 0 в ядре струи скорость частиц v, а длина струи l_o ≈ 5 h. Толщина прмежуточной зоны при х ≤ l_o может быть оценена по формуле δ = 0,1х при х ≤ В.

Рис. 6.2 – Характер течения жидкости в каналах

с впадинами

За пределами струи возникают зоны замкнутого циркуляцион­ного движения. Для глубоких или широких впадин характерно образование вто­ричных циркуляционных токов. Используя зависимости для тепло­обмена в гладких каналах, некоторые выводы из теории струйных течений, а также результаты экспериментальных исследований, можно предложить упрощенную схему расчета среднего числа Нуссельта 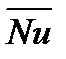для канала со впадинами и выступами; при этом число обозначает безразмерный комплекс:

; ; ,

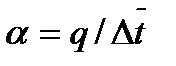где h_э – эквивалентная схема канала; t, t_w – средняя массовая температура жидкости и температура стенок канала на расстоянии x; q – средняя плотность теплового потока, отнесенная к размеру L = B + D канала.

Если канал образован одинаковыми платами с поперечными впадинами на обеих сторонах, то согласно формуле (16.1) для эквивалентного диаметра d_э=2h_э:

h_э = [2H b + h (b + d)]/(2H + b + d).

Если одна стенка канала гладкая, а другая имеет впадины и выступы, то:

h_э = [H b + h (b + d)]/(H + b + d).

Среднее значение числа в таких каналах:

,

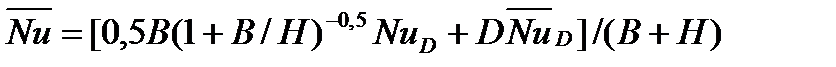где Nu_D и 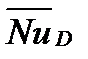- локальное при x = D и осредненное по длине числа Нуссельта, определяемые по формулам (16.5) и (16.6).

Начальная длина l_н определяется по формулам:

при B≥5hl_н= 00,1 h Re; при B<5hl_н = 4·10^-3 B Re.

Для каналов с продольными и поперечными впадинами и 0≤ b/d ≤2:

l_н = 2·10^-3 h (1+4 b/h_э)(B/H)Re.

Предлагаемая схема расчета числа не применима для кана­лов, у которых D<<B. Для каналов только с поперечными впадина­ми при B≤D расхождение данных расчета и опыта 5—10%; для каналов с поперечными и продольными впадинами — не более 20%.

При числах Re>3000 впади­ны интенсифицируют теплообмен и при расчете α нельзя пользо­ваться формулами для гладкого канала с введением в них, как при­нято, эквивалентного диаметра по формуле (16.1), так как ошибка может превысить 100%. При Re<2·10³, несмотря на увеличение площади теплоотдающей поверхности каналов с выступами, интен­сивность теплообмена не отличается от гладких каналов с тем же эквивалентным диаметром.

Поиск по сайту: