Вынужденная конвекция при внешнем обтекании тела. Продольное движение потока жидкости

Продольное движение потока жидкости. Пусть внешняя поверх­ность тела омывается потоком жидкости, имеющим на удалении от тела скорость v. Существует три режима движения жидкости — ламинарный, переходный и турбулентный. Переходный режим занимает малую область, и расчеты, как прави­ло, ведутся на два режима движения жидкости — ламинарный и турбулентный.

Коэффициент теплоотдачи при вынужденном движении жидко­сти представляются обычно в виде зависимости между числами Нуссельта Nu_f, Рейнольдса Re_f и Прандтля Pr_f или Рr_w:

Nu_f = αl/λ_f, Re_f = vl/ν_f, Pr_f = ν_f/a_f, Pr_w = ν_w/a_w. (15.1)

где индексы f и w означают, что соответствующие параметры рассматриваются при температурах жидкости t_f и стенки t_w; l – длина тела по направлению потока.

Переход от ламинарного к турбулентному определяется критическим значением числа Re_кр, которое при продольном обтекании плоской стенки обычно принимают Re_кр = 5·10⁵.

При ламинарном движении жидкости, т.е. Re_f < 5·10⁵, критериальное уравнение для среднего коэффициента теплоотдачи имеет следующий вид:

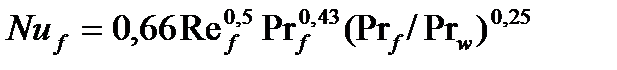. (15.2)

За определяющую температуру здесь принята температура набега­ющего потока t_f,за определяющий размер — длина теплоотдающей стенки по направлению потока. Влияние физических свойств жид­кости и их зависимость от температуры учитываются параметром Рr_f^0,43, а влияние направления теплового потока (от жидкости к стенке или наоборот) и род жидкости — параметром (Pr_f/Pr_w)^0,25, для газов этот параметр равен единице.

Для воздуха в интервале температур (от 0 до 1000^оС) можно считать Pr_f = Pr_w = 0,70, а (Pr_fw)^0,43 = 0,86 и тогда формула (15.2) примет вид:

.

При значениях Re, превышающих критическое или равное ему (Re_f ≥ 5·10⁵), возникает турбулентное течение и критериальное уравнение для среднего коэффициента теплоотдачи имеет вид:

(15.3)

Или в более простой форме:

/

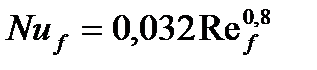Определяющая температура и размер как и в предыдущем случае.

Приведенные выше формулы были получены при исследовании теплообмена плоской плиты, омываемой потоком жидкости. В приближенных расчетах можно использовать эти формулы и для оп­ределения теплообмена цилиндрических поверхностей, омываемых продольным потоком жидкости.

Поперечное движение потока воздуха. Ниже рассмотрен метод определения коэффициента теплоотдачи тел различной формы, омываемых поперечным потоком воздуха. Для тел разнообразной конфигурации целесообразно ввести характерный размер, опреде­ляемый по какому-нибудь единому принципу, а именно в качестве характерного размера выбирается длина обтекания l’ тела потоком воздуха. Длина обтекания для цилиндра и шара составляет l' = 0,5πd,а для пластины — l' = l (рис.15.1). В этом случае числа Рейнольдса и Нуссельта определяют следующим образом:

Re’ = vl’/ν_f, Nu’ = αl’/λ_f.

При значениях числа Рейнольдса 10 < Re’ < 10⁵ уравнение подобия для теплоотдачи тел, омываемых поперечным потоком воздуха, с ошибкой не более 20% может быть представлено в виде:

. (15.4)

Формулу (15.4) можно использовать также для оценки коэф­фициента теплоотдачи тел, находящихся в замкнутом пространст­ве и омываемых поперечным потоком воздуха. Определяющим раз­мером в этом случае также будет l', а скорость движения воздуха около тела можно определить по формуле:

, (15.5)

где G_V — объемный расход воздуха, протекающего через ограни­ченное пространство; А_ср — площадь среднего сечения потока, т. е. средняя площадь пространства между телом и ограничивающей его оболочкой (корпусом).

Для электронных аппаратов с хаотическим расположением де­талей параметры A_cр и l могут быть оценены по формулам:

, , (15.6)

где А_ап – площадь сечения пустого корпуса аппарата в направлении, нормальном к потоку; V и V_д – объем пустого корпуса и суммарный объем всех деталей, шасси и других твердых тел в нагретой зоне; l_j, A_j – длина траектории потока около детали j и площадь теплоотдающей поверхности этой детали.

Поиск по сайту: