Свободная конвекция в ограниченном пространстве

Сложный процесс теплообме­на в ограниченном замкнутом пространстве принято рассматри­вать по аналогии с передачей теплоты путем теплопроводности, что позволяет избежать определения коэффициентов теплоотдачи на­гретой и холодной поверхностей. С этой целью вводится понятие об эквивалентной теплопроводности λ_эксреды между поверхностями теплообмена. Описание процесса проводят с помощью критериаль­ного уравнения:

ε_к = λ_эк/λ_f = f(Gr·Pr)_f, (14.1)

где ε_к – коэффициент конвекции; λ_f – теплопроводность жидкости в прослойке при среднеарифметической температуре t_m стенок.

Тепловой поток для прослоек различной формы, заполненных твердым материалом, можно найти из формулы:

Ф = Δt/F = α_12пAΔt, Δt = t₁ – t₂, (14.2)

Применим её для описания процесса переноса теплоты через прослойку, заполненную жидкостью или газом. Здесь через α_12п обозначен эффективный коэффициент теплоотдачи, объединяющий коэффициенты теплоотдачи на нагретой и холодной поверхностях.

Выражения для эффективных коэффициентов теплоотдачи в прослойках различной конфигурации имеют вид:

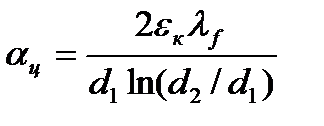, , . (14.3)

Если средой является сухой воздух, то анализ приведенных выше формул приводит к следующим практическим выводам. В узких прослойках при не­больших перепадах темпе­ратур Δt между поверхно­стями свободная конвекция отсутствует и теплота пере­носится через среду только теплопроводностью. Например, в воздуш­ных прослойках, когда δ > 10 мм, конвекция начина­ется даже при Δt = 0,3 К; в прослойках до δ = 10 мм на­чало конвекции имеет место при Δt >5 К, а в слоях с δ < 5 мм конвекция отсутствует вплоть до Δt = 100 К.

Рассмотрим процесс конвективного теплообмена внутри ограниченного объема, имеющего форму параллелепипеда, одна грань которого с размерами l₁, l₂ находится при температуре t₁ а остальные — при t₂,причем t₁>t₂ (рис. 14.1, а).Эффективный ко­эффициент теплоотдачи через такую заполненную воздухом про­слойку:

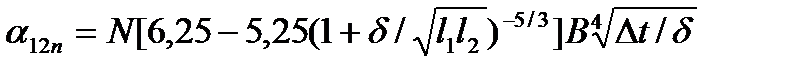, (14.4)

где δ – толщина прослойки; N = 1 и N = 1,3 – коэффициенты для вертикальной и горизонтальной ориентации соответственно; при горизонтальной – нагретая грань находится снизу. Коэффициент В зависит от средней температуры воздуха t_m = 0,5(t₁+t₂).

Интенсивность теплообме­на в замкнутых прослойках можно более детально описать с по­мощью локального коэффициента конвекции:

ε_кл = (q – q_л)q_т, (14.5)

где q – суммарная плотность теплового потока; q_л, q_т – плотности тепловых потоков вследствие излучения и молекулярной теплопроводности.

Установлено, что интенсив­ность локального теплообмена в замкнутых вертикальных про­слойках высотой h с изотерми­ческими стенками может изме­няться по высоте почти в 10 раз. При этом характерны три зоны (рис 14.2): в нижней час­ти прослойки (x/h) < 0,2 ε_кл имеет максимальное значение, далее с ростом' отношения x/h ε_кл уменьшается до едини­цы, потом остается неизмен­ным и, наконец, в верхней зоне (x/h) < 0,7 может достигать значений ε_кл < 1, доходя до 0,2. Движение газа вдоль нагретой пластины вызвано повышением его температуры. С ростом х увеличивается толщина погра­ничного слоя и падает перепад температур между пластиной и воздухом, что приводит к уменьшению плотности тепло­вого потока q. В верхней зоне эта разность может оказаться столь малой, что передача энергии от нагретой пластины к холодной будет проходить в основном за счет плотности по­тока излучения q_л и может оказаться, что (q – q_л) < q_т. Обработка результатов измерений для прослойки высотой h и шириной δ привела к уравнениям подобия, связывающим локальный коэффициент конвекции ε_кл с числом Рэлея Ra = Gr·Pr и отношением δ/h при нормальном давлении р = 10⁵ Па:

ε_кл = 2,25 lg Ra_m – 4,8x/h – 5,57; Ra_m = Gr_m·Pr_m,(14.6)

1 ≤ Ra_m ≤ 10⁵, 0,025 ≤ (δ/h) ≤ 0,175, p = 10⁵ Па, ε_кл ≥ 1.

Значения , начиная с которого ε_кл < 1, равно

х_кр = 1 для 0 < lg Ra_m ≤ 3; х_кр = 0,77 для 3 < lg Ra_m < 4,5.

Значения физических параметров среды в формулах берутся для средней температуры

t_m = 0,5(t₁+t₂).

Участки с пониженной интенсивностью теплообмена могут занимать до 25% общей высоты прослойки и располагаться в верхней части нагретой и нижней части холодной пластин.

Вертикальный канал. Возьмем плоский вертикальный незамкнутый канал, высота и глубина которого h и B, ширина b; стенки канала одинаково нагреты и имеют на расстоянии х от входа в канал температуру t_w(x). Из-за разности температур между воздухом внутри канала t_f(x) и вне его t_f(0) = t_c возникает свободная конвекция.

Для плоского вертикального канала с изотермическими стенками и воздушной средой рекомендуются следующие формулы для расчета среднего коэффициента теплоотдачи α и скорости воздуха v:

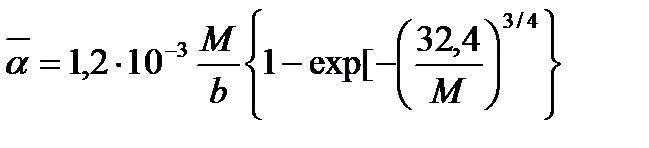; (14.7)

,

где - средние температуры стенки и среды;

; ,

где α = 0,115/b – локальный коэффициент теплоотдачи.

Теплообмен при давлениях, отличных от нормального. Конвек­ция в неограниченном пространстве, в ограниченных прослойках и незамкнутых каналах зависит от давления газа. Если конвектив­ные коэффициенты теплоотдачи и проводимости при нормальном давлении p_o обозначить через α_к и σ_к, а при давлении р — через α_кри σ_кр,то между этими параметрами при 10²<р<10⁶ Па суще­ствует следующая связь:

α_кр = α_к (p/p_o)²ⁿ, σ_кр = σ_к (p/p_o)²ⁿ, (14.8)

Эта зависимость справедлива также и для вынужденного движения газа.

Поиск по сайту: