Уравнение теплопроводности. Начальные и граничные условия

Дифференциальные уравнения теплопроводности имеет бесчисленное множество решений. Для выделения единственного решения этого уравнения, соответствующего единственному явлению теплопроводности, должны быть заданы следующие параметры:

1. Геометрические размеры и форма тела, а также время τ для нестационарного процесса. Заметим, что время процесса может быть задано неявно по какому-либо дополнительному условию, например, нагрев или охлаждение тела до достижения теплового равновесия с окружающей средой;

2. Физические свойства вещества (коэффициент теплопроводности λ, удельная объемная теплоемкость с' (или удельная массовая теплоемкость с), плотность ρ, коэффициент температуропроводности a);

3. Закон распределения внутренних источников теплоты q_v (x_i, τ). В частном случае ;

4. Краевые условия задают начальное распределение температуры в заданной расчетной области и условия теплообмена на границе этой области.

Перед началом расчета процесса нестационарной теплопроводности необходима информация о распределения температуры в объеме тела в некоторый момент времени, принимаемый за начало отсчета, или начальный момент времени (момент времени τ = 0). Т.о., должна быть задана функция

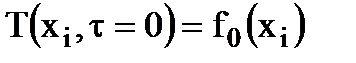или ,

где – система координат.

В частном случае одномерного и равномерно распределенного в объеме тела начального температурного поля НУ имеют вид:

Т (х, 0) = Т₀ = const.

Заметим, что для задач стационарной теплопроводности задание начальных условий не имеет смысла.

В расчетах теплообмена применяют четыре типа ГУ, которые называют родами. Граничные условия теплообмена необходимо задавать, как на внешней поверхности тела (внешние ГУ), так и, при расположении границы расчетной области внутри тела, на внутренней поверхности (внутренние ГУ). Граничные условия первого и второго родов могут быть как внешними, так и внутренними, граничные условия третьего рода – только внешние граничные условия, граничные условия четвертого рода – только внутренние граничные условия.

Граничные условия первого рода

При граничныхусловиях I рода задают значение температуры на границе расчетной области:

,

где индекс w означает "граница"; 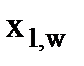– координаты границы заданной расчетной области. В частном случае эта температура после мгновенного изменения до температуры T_w может оставаться неизменной во времени и не изменяться вдоль границы:

.

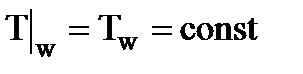Граничные условия второго рода

При граничных условиях II рода задают значение плотности теплового потока на границе расчетной области:

,

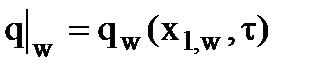где индекс w означает "граница"; 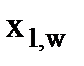– координаты границы заданной расчетной области.

С учетом закона Фурье ГУ II рода можно записать следующим образом

,

где n – координата, направленная по нормали к границе расчетной области.

В частном случае плотность теплового потока q_w может не изменяться вдоль границы расчетной области и быть постоянной во времени:

.

Граничные условия третьего рода

При граничных условиях III рода задают температуру внешней среды, окружающей тело, и закон теплообмена между средой и поверхностью тела. Граничные условия третьего рода являются наиболее общими и часто используемыми в практике расчетов граничными условиями. В качестве закона теплообмена между окружающей тело средой и поверхностью тела наиболее часто в инженерных расчетах используют закон теплоотдачи – закон Ньютона

где – коэффициент теплоотдачи (вспомним, что в общем случае теплоотдача происходит конвекцией и излучением); T _f – температура флюида; T_w – температура поверхности тела.

С учетом закона Фурье ГУ III рода можно записать следующим образом

,

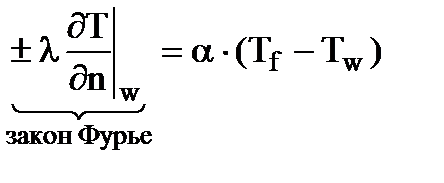где знак + или – в законе Фурье зависит от выбора начала системы координат.

В расчетах теплопроводности используют безразмерную форму записи граничных условий третьего рода

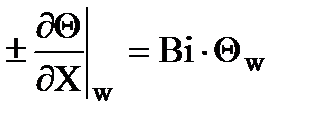, где 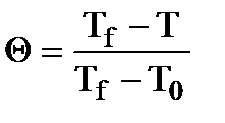– безразмерная температура; – безразмерная координата, перпендикулярная поверхности теплообмена; R – характерный или определяющий размер тела; 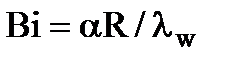– критерий Биó (Biot); λ_w – коэффициент теплопроводности твердого тела.

Критерий Био – определяющий критерий в задачах теплопроводности, т.е. от его величины зависит интенсивность процесса теплопроводности. Физический смысл критерия Био можно раскрыть, записав его формулу в виде

,

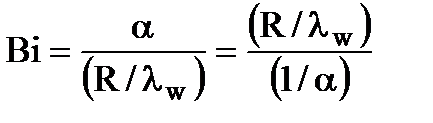т.е.критерий Био характеризует:

а) отношение интенсивности внешнего теплообмена (a) к интенсивности внутреннего теплообмена(l/R);

или

б) отношение термического сопротивления теплопроводности(R/l) к термическому сопротивлению конвективной теплоотдачи(1/a).

Граничные условия четвертого рода

Граничные условия IV рода задают условия теплообмена на границе идеального контакта двух тел, состоящих из разного вещества с разными физическими свойствами. В этом случае в зоне идеального контакта у обоих тел равны температуры и тепловые потоки

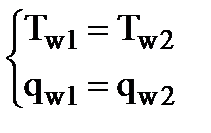, или, используя закон Фурье .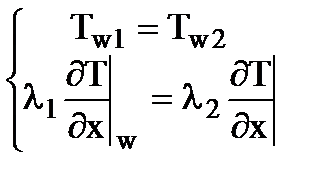

Поиск по сайту: