Нестационарная теплопроводность. Классификация процессов

В случае, когда температура во всех точках системы изменяется с течением времени, поле температур называется нестационарным.

Все процессы нестационарной теплопроводности в зависимости от характера изменения температуры во времени разделяются на три класса:

1) переходные процессы – температура в каждой точке тела изменяется от одного установившегося значения до другого;

2) процессы непрерывного нагрева (охлаждения) – неограниченное изменение температуры во времени или в пространстве;

3) периодические процессы – температура колеблется около некоторого значения.

Рассмотрим тело произвольной конфигурации, которое в начальный момент времени τ=0 имеет температуру t₀, объемную плотность теплового потока q_v и начальную температуру среды t_с(0)=t_cо. Тело вносится в среду, тем­пература t_с(τ) которой изменяется во времени; теплообмен тела со средой подчиняется закону Ньютона (dФ=αΔtdA), Задача состоит в определении температуры тела в любой момент времени. Темпера­турное поле такого тела полностью описывается дифференциаль­ным уравнением (4.6), граничным условием (4.6) и приведенны­ми выше начальными условиями. После преобразований получим выражение:

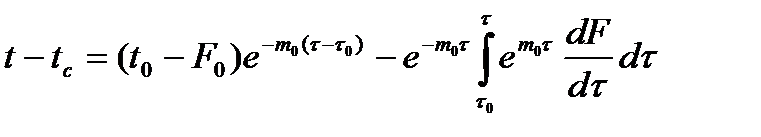, (9.1)

F₀ = t_co+Ф₀ /(m₀ C), F =t_c+Ф/(m₀ C).

где Ф – полная тепловая мощность источников теплоты в теле.

Дальнейший анализ можно проводить, если задан вид функциональных зависимостей t_c=t_c(τ) и Ф=Ф(τ). Здесь возможны различные сочетания.

Постоянная температура среды. Пусть Ф = 0 и тело помещено в среду с постоянной температурой t_c = const и зависимость (9.1) можно представить в виде:

. (9.2)

Из этого выражения следует, что разность температур тела и среды изменяется по закону экспоненты (рис. 9.1, а). Прологарифмировав формулу (9.2) получим:

ln θ =m₀(τ – τ₀) = –m₀τ + const. (9.3)

На рис. 9.1, б дано графическое представление этой зависимости в полулогарифмических координатах. Из этого рисунка и формулы (9.3) следует, что:

m₀= (ln θ₁ – ln θ₂) / (τ₂ – τ₁) = [ln(t₁ – t_c) – ln(t₁ – t₂)]/(τ₂ – τ₁). (9.4)

Это выражение позволяет определить опытным путем параметр m_o, который называется темпом охлаждения (нагревания) тела (1/c).

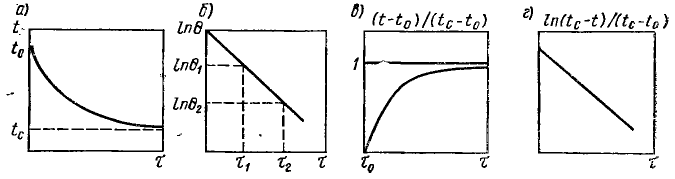
Рис. 9.1 – Графики изменения температуры тела в среде с постоянной температурой:

а, б – охлаждения; в,г - нагревания

Допустим из опыта получена зависимость t–t_c= f(τ); построив ее в полулогарифмических координатах ln[(t – t_c)/(t_o – t_c)] = f₁ (τ) и выбрав два каких-либо момента времени τ₁ и τ₂, находим по формуле (9.4) m _o.

Рассмотрим нагревание тела в среде t_c> t_o. Вычтя из правой и левой части уравнения (9.2) по единице, после преобразования получим:

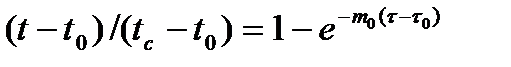. (9.5)

Графическая зависимость (9.5) представлена на рис. 9.1,в. Выражение (9.5) с помощью тождественных преобразований можно представить в виде:

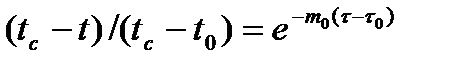; (9.6)

На рис. 9.1,г дано графическое представление (9.6) в полулогарифмических координатах.

Темп нагревания тела по аналогии с темпом охлаждения можно определить по формуле:

m₀= [ln(t_с – t₁) – ln(t_с – t₂)]/(τ₂ – τ₁). (9.7)

При простом нагревании или охлаждении тела с равномерным полем температуры темпы нагревания и охлаждения численно равны между собой.

Температура среды изменяется во времени с постоянной скоростью.

Рассмотрим случай (Рис. 9.2):

t_c =b(τ – τ_o)+t_co, Ф =Ф_o, b =dt_c/dτ = const.

Согласно (9.1), F_o =t_co, F =t_c, после преобразования получим

.(9.8)

Графическое представление разновидностей рассматриваемых режимов дано на рис. 9.2, из которого видно, что возможны слу­чаи пересечения кривых t(τ) и t_с(τ), однако такое пересечение мо­жет быть только в одной точке.

Рассмотрим как изменяется ход кривой t(τ) с течением времени. Второе слагаемое в (9.8), содержащее экспоненту exp[-m_o(τ – τ_o)] в качестве множителя, становится при больших τ пренебрежительно малым по сравнению с первым, т.е. разность температур тел и среды стремится стать постоянной

t – t_c = - b/m_o (9.9)

при больших значениях (τ – τ_o). Из рис. 9.2 видно, что с течением времени кривые t(τ) и t_с(τ) становятся практически параллельными. Обозначим τ_о время, начиная с которого с заданной степенью точности можно не учитывать второе слагаемое в (9.8), тепловой режим тела при τ > τ_p будет называться регулярным режимом II рода, а при τ < τ_p – иррегулярным режимом.

Из анализа рис. 9.2 следует, что для всех случаев соотношений t_o и t_co при τ > τ_p разность температур t_p – t_c изменяется по одинаковому закону (9.9). В развернутом виде это уравнение имеет вид

t_p = t_co+b(τ – τ_o) – b/m_o, b><0. (9.10)

Данное выражение является приближенным решением задачи, что удобно для решения некоторых технических задач.

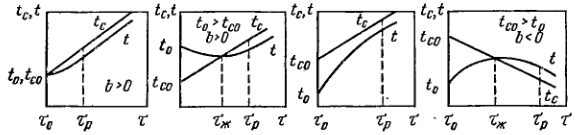
Рис. 9.2 – графики изменения температуры тела в среде с линейно меняющейся температурой

Температура среды изменяется по гармоническому закону. Простейший закон периодического изменения температуры среды имеет вид:

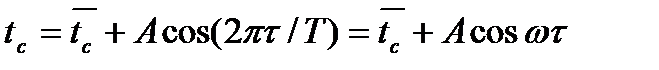, (9.11)

где t_c – среднее значение температуры среды, около которого происходят ее колебания; Т – период колебаний; А – амплитуда колебаний; ω = 2π/T – частота.

Применив общую формулу (9.1), в которой F=t_c, F_o=t_co, F’= - A cos ωτ, после преобразования получим:

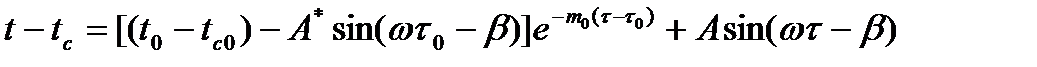; (9.12)

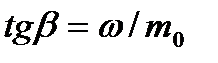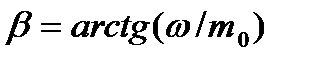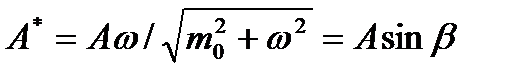, , . (9.13)

Через некоторое время от начала процесса экспоненциальный сомножитель в (9.12) может оказаться столь малым, что первым членом в (9.12) можно будет пренебречь, тогда:

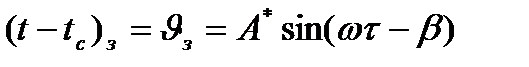. (9.14)

Индекс «р» означает, что рассматривается только та часть процесса, в которой начальное температурное состояние (t_o, t_co), а также момент фиксации начала процесса τ_o уже не играют роли, т.е. изучаемый процесс вступил в наиболее простую (регулярную) стадию. Этот температурный режим называют в литературе регулярным режимом III рода.

Рис. 9.3 – Температура тела t в среде с гармонически меняющейся температурой t_c среды

Сравним колебания температур t_c и t около среднего значения t_c (рис. 9.3). Для этого в последней формуле заменим t_c его выражением из (9.11), а вместо А^* запишем A sin β; тогда получим

;

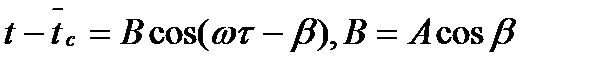. (9.15)

Из (9.15) следует, что амплитуда В колебаний системы в cosβ раз меньше амплитуды А колебаний температуры среды; отстава­ние по фазе системы дано величиной β, которая зависит от периода колебаний Т и параметра m_o.

Рассмотренные выше три случая изменения температуры тела в среде с переменной во времени температурой нашли широкое при­менение в задачах о тепловой инерции различных технических уст­ройств.

Величину, обратную m_o называют показателем тепловой инерции: ε_и = 1/m_o = C/(αA).

В случае если t = const, то параметр ε_и определяет быстроту приближения системы к тепловому равновесию со средой.

Изложенная теория справедлива не только для однородного тела, но и для системы тел, если температурное поле системы тел равномерно.

Еще один важный параметр, характеризующий инерционные свойства тела – время z установления системы, по истечении которого разность (t – t_c) температур системы и среды станет меньше заданного значения Δ.

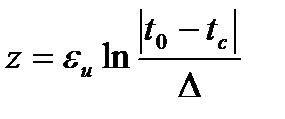. (9.16)

Нагревание тела внутренними источниками энергии. Пусть t_c = const, Ф = const, тогда температура t в любой момент времени:

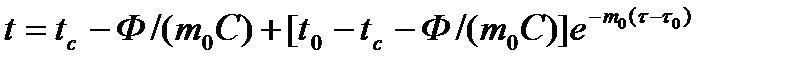
При τ→∞ наступит стационарный режим и температура тела станет равной

Для t формула примет вид:

. (9.17)

Эта формула аналогична формуле (9.6) для простого нагревания тела в среде с более высокой температурой.

Поиск по сайту: