Стационарное поле температур тела с источниками энергии

Неограниченная пластина. Температурное поле в пластине ме­няется только в направлении х, поэтому в уравнении (4.8) d²t/dy²=d²t/dz²=0, что позволяет представить это уравнение в форме:

,

решение которого:

.

Пусть на границах x=±L коэффициенты теплоотдачи α одина­ковы, а температуры t_c сред, омывающих поверхности пластины, равны друг другу. В этом случае температурное поле в теле будет симметричным относительно оси x = 0, т. е. в центре пластины сле­дует ожидать максимального значения температуры, что позволяет записать условие симметрии .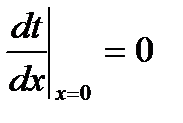

Условия симметрии на границе x = L позволяют найти постоянные интегрирования

С₁ = q_vL/λ, C₂ = t_c + q_vL/α и получить окончательное решение:

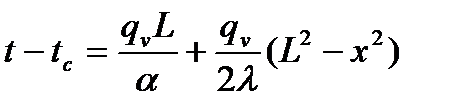. (6.1)

Неограниченный цилиндр. Система уравнений температурного поля неограниченного цилиндра с внутренним источником теплоты, с учетом симметрии поля относительно оси:

.

Решение дифференциального уравнения:

.

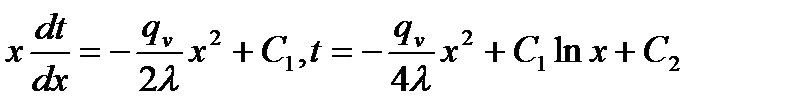Следует обратить внимание, что при х= 0t=-∞, что абсурдно, поэтому полагаем постоянную интегрирования C₁ = 0. Вторую постоянную С₂ найдем из условия на границе x=L;окончательно получим:

. (6.2)

Параллелепипед. Часто требуется определить лишь максималь­ную температуру параллелепипеда. Если источники распределены по всему объему равномерно, то максимальная температура будет в центральной точке.

Будем полагать, что температура граней одинакова и равна средней поверхностной температуре t_A. Температуру t₀ в центре параллелепипеда представим как перегрев t₀ – t_A относительно поверхности. Это позволяет записать на гранях параллелепипеда граничные условия I рода:

(t – t_A)_x=±lx = (t – t_A)_y=±ly = (t – t_A)_z=±lz = 0.

Дифференциальное уравнение теплопроводности примет вид:

.

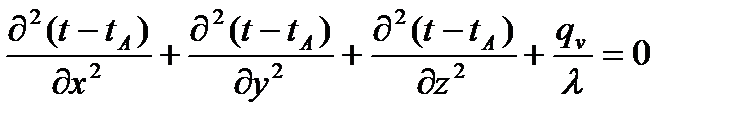Для центра параллелепипеда температура t ₀ рассчитывается по формуле:

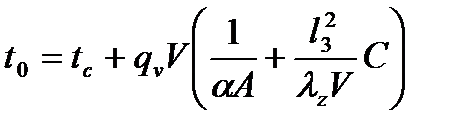или (6.3)

где А – площадь, V – объем, l₃ – длина грани параллелепипеда, С – коэффициент, связанный с параметрами l₃/l₁, l₃/l₂ (l₁ =√λ_z/λ_x, l₂ =√λ_z/λ_y, l₃ = l_z).

Поиск по сайту: