Термическое сопротивление стенок: плоская, цилиндрическая, сферическая, составная, оребренная

Однородные стенки. На рис. 8.1 изображены однородные стенки плоской, цилиндрической и сферической конфигурации, поверхности которых х=l₁ и x=l₂ являются изотермическими с температурами t₁ и t₂,а торцы пло­ской и цилиндрической стенок являются адиабатными; внутрен­ние источники теплоты в стенке отсутствуют, теплопроводность ма­териала — λ. Найдем выражение для стационарного теплового по­тока Ф, проходящего через эти стенки.

Воспользуемся зависимостями (7.1), связывающими разность температур (t₁—t₂) с тепловым потоком Ф, а значение термическо­го коэффициента F найдем для каждого конкретного случая с по­мощью выражения (7.4).

Элемент длины dl пути теплового потока для плоской, цилинд­рической и сферической стенок равен dl=dx, а аналитические выраже­ния для А(х) изотермических поверхностей имеют такой вид: A_n=L₁L₂, А_ц=2πхL_ц, А_с=4πх², где L₁ и L₂ — длина и ширина пло­ской стенки; L_ц — длина цилиндрической стенки.

Поскольку по условиям задачи между изотермическими поверх­ностями отсутствуют источники и стоки энергии, коэффициент F имеет смысл термического сопротивления, которое для плоской, цилиндрической и сферической стенок обозначим R_п, R_w, R_c. Учитывая неизменность потока теплоты Ф(x) =const и подставляя значения dl и A(x) в выражения (7.4), получим:

;

; (8.1)

.

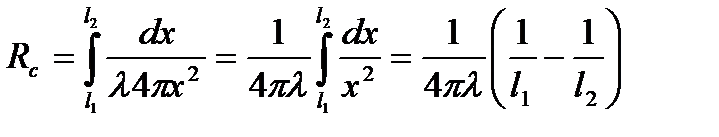Рис. 8.1 – К расчету теплового сопротивления плоской а), цилиндрической б) и сферической в) стенок

Составные стенки. Рассмотрим теперь последовательно состав­ленную плоскую стенку, состоящую из п разнородных, ориентиро­ванных перпендикулярно тепловому потоку слоев, толщины и теплопроводности которых δ_i и λ_i; температуры наружных поверхностей стенок равны t₁ и t_n+1 (рис. 8.2, а).

Изотермическими поверхностями в этом случае являются пло­скости, параллельные поверхности стенок. Между изотермическими поверхностями отсутствуют стоки и источники энергии, и тепловой поток, не изменяясь, проходит через все стенки. Следовательно, каждой стенке можно приписать термическое сопротивление R_i; все термические сопротивления, как это видно из рис. 8.2, б, со­единены последовательно, т. е. суммарное термическое сопротивле­ние:

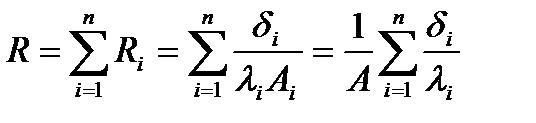. (8.2)

На основании (7.1) между температурами t₁ и t_n+1 и тепловым потоком Ф справедлива зависимость:

. (8.3)

Рис. 8.2 – Последовательное соединение плоских стенок (а) и их тепловая схема(б)

Для термических сопротивлений последовательно составленных цилиндрической и сферической неоднородных стенок, состоящих из n различных слоев, расположенных перпендикулярно тепловому потоку:

; (8.4)

, (8.5)

где l_i – радиус i-го цилиндрического или сферического слоя; L_ц – длина цилиндра.

Термическое сопротивление теплоотдачи можно уменьшить, если со стороны меньшего коэффициента теплоотдачи увеличить поверхность теплообмена за счет ее оребрения. Для доказательства этого утверждения запишем единую формулу теплопередачи при допущении малости термического сопротивления теплопроводности ()

.

Пусть . Откуда следует, что при равенстве площадей термическое сопротивление теплоотдачи около второй поверхности много больше термического сопротивления теплоотдачи около первой поверхности

или .

Поэтому для уменьшения необходимо увеличить площадь S₂ до выполнения условия

или ,

где – площадь оребренной поверхности.

Профиль ребра может быть прямоугольной, треугольной, трапециевидной и, в общем случае, произвольной формы (рис. 8.3).

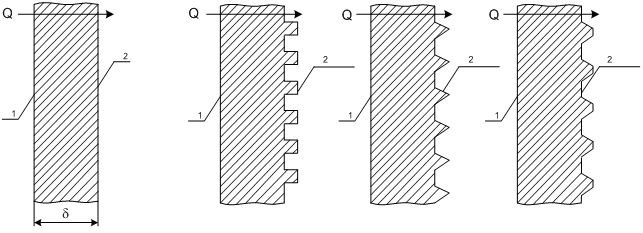
Рис. 8.3 - Конструктивный способ интенсификации теплопередачи

за счет оребрения поверхности

Поиск по сайту: