Свободная конвекция в неограниченном пространстве

Сопоставляя и обобщая на основе теории подобия обширный экспериментальный материал по теплообмену при естественной конвекции в неограниченном пространстве, исследователи предложили общую зависимость для коэффициента теплообмена тел с одним определяющим размером (вертикальные плиты, бесконечно длинные проволоки, трубы и шары). Приведём получившие большое распространение формулу,
предложенную акад. М.А. Михеевым.

nNum = C (Gr ⋅ Pr) m (13.1)

где с и n – эмпирические коэффициенты, а индекс m указывает, что значения физических параметров λ, а,ν, β газа или жидкости следует выбирать для средней температуры tm рассчитываемой по формуле tm = 0,5(tw + tc). Постоянные с и n в формуле (13.1) зависят от величины аргумента (Gr ⋅ Pr)

По величине коэффициента с и n различают четыре случая теплообмена, соответствующие четырем режимам движения:

1) так называемый пленочный режим, при котором у поверхности образуется практически неподвижная пленка нагретой жидкости (с =0,5; n=0):

(13.2)

Рис.13.1. Характер теплообмена при различных режимах

В этом случае коэффициент теплообмена прямо пропорционален теплопроводности среды. Такой режим неустойчив и наблюдается у тел с плавными очертаниями при небольших температурных напорах (рис 13.1,а);

2) при 5 ⋅102 > (Gr ⋅ Pr) > 10−3 a)наступает переходный режим, у стенок тела образуется пограничный слой, в котором наблюдается слабое ламинарное движение (рис. 4.1, б), в данном случае с =1,18, n =1/8;

3) при 2⋅107 > (Gr ⋅ Pr) > 5⋅102 устанавливается основной ламинарный режим движения; здесь с =0,54, n =1/4 (закон 1/4). Такой режим движения жидкости наступает около омываемых плоскостей, цилиндров и шаров, размеры которых изменяются в пределах от нескольких сантиметров до десятков сантиметров при средних температурных напорах (10 < Δ t < 200 K) (рис. 13.1, в);

4) наконец, при 1013> (Gr ⋅ Pr)> 2 ⋅107, с =0,135, n=1/3 наступает вихревой турбулентный режим движения жидкости или газа (рис. 13.1, г) (закон 1/3) интенсивным теплообменом.

Заметим, что формула (13.1) получена на основании обобщения
опытов, приводящихся в различных средах (воздух, водород, углекислота, глицерин, вода, различные масла и др.), с разнообразными объектами
исследования (горизонтальные и вертикальные проволоки, трубы, плиты, шары), размеры которых изменялись в широких пределах (от проволок с
L=1,55 мм до шаров с L=16 мм). При вычислении критериев подобия за определяющий размер принимался для труб и шаров их диаметр d, а для плит – их высота h.

Рис. 13.2. Критериальные зависимости при свободном движении

Тот факт, что данные, полученные из опытов с телами разнообразной
формы в критериальных координатах укладываются на одну кривую, позволяет сделать следующий вывод: форма тела слабо влияет на характер теплообмена при естественной конвекции; режим движения жидкости, в основном, определяется размером тела, свойствами среды и температурным напором.

Рассмотрим подробнее структуру выражения (13.1) для случая
вихревого движения, т.е. n =1/3:

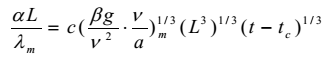
или

Можно заметить, что в этом режиме коэффициента теплообмена не зависит от размеров тела. Такой процесс называют автомодельным. Исследования показали, что формула (13.1) может использоваться и для расчета коэффициента теплообмена горизонтальных плит. В этом случае за определяющий размер берется не высота, а меньшая сторона плиты. Расчетная величина коэффициента теплообмена увеличивается на 30%, если поверхность теплообмена обращена вверх, и уменьшается на 30%, если поверхность теплообмена обращена вниз,т.е. (Nu _в) _m = 1,3 (Nu) _m; (Nu_Н)_m= 0,7(Nu)_m

Следует обратить внимание на тот факт, что формула (13.1) не чувствительна к направлению теплового потока. Например, коэффициент теплообмена, вычисление для случаев t = 100 ºС, tc = 20 ºС и tc = 20 ºС, t = 100 ºС, будут численно равными. Однако опыт показывает, что направление теплового потока влияет на величину коэффициента
теплообмена. Это влияние, по предложению М.А.Михеева, учитывается дополнительным множителем K в уравнении (13.1), а именно:

(4.3)

где критерии Prc – рассчитывается по определяющей температуре, равной
температуре среды tc, Pr w – для температуры стенки tw. При нагревании жидкости t > tc тепловой поток направлен от стенки к среде (Pr c / Pr w) > 1, а при охлаждении t<t_c(Pr_c/Pr_w)_охл, т.е. αн > α_охл, причем разность αн и α_охл возрастает по мере увеличения температуры.

Формулы в критериальном виде не всегда удобны для практического применения, поэтому на основе критериальных формул составляются рабочие формулы для расчета коэффициента теплообмена. Например, если для плоской и цилиндрической поверхности выполняется условие

|t-t_c|≤(840/L)³ (13.4)

То движение жидкости подчиняется закону ¼ степени. Здесь L – определяющий размер тела в миллиметрах.

Рассмотрим следующие рабочие формулы для расчета конвективного коэффициента теплообмена при законе n =¼ для вертикально ориентированной поверхности высотой h (в метрах).

Вт/М² (13.5)

Поиск по сайту: