Соотношение неопределенностей Гейзенберга для координаты и импульса. Волновая функция и ее физический смысл

Согласно двойственной корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойства частиц и все свойства волн нельзя. Естественно, что необходимо внести некоторые ограничения в применении к объектам микромира понятий классической механики.

В классической механике состояние материальной точки (классической частицы) определяется заданием значений координат, импульса, энергии и т.д. (перечисленные величины называются динамическими переменными). Строго говоря, микрообъекту не могут быть приписаны указанные динамические переменные. Однако, информацию о микрочастицах мы получаем, наблюдая их взаимодействие с приборами, представляющими собой макроскопические тела. Поэтому результаты измерений поневоле выражаются в терминах, разработанных для характеристики макротел, т.е. через значения динамических характеристик. В соответствии с этим измеренные значения динамических переменных приписываются микрочастицам. Например, говорят о состоянии электрона, в котором он имеет такое-то значение энергии, и т.д.

Волновые свойства частиц и возможность задать для частицы лишь вероятность ее пребывания в данной точке пространства приводят к тому, что сами понятия координаты частицы и ее скорости (или импульса) могут применяться в квантовой механике в ограниченной мере. В этом, вообще говоря, нет ничего удивительного. В классической физике понятие координаты в ряде случаев тоже непригодно для определения положения объекта в пространстве. Например, не имеет смысла говорить о том, что электромагнитная волна находится в данной точке пространства или что положение фронта волновой поверхности на воде характеризуется координатами x, y, z.

Корпускулярно-волновая двойственность свойств частиц, изучаемых в квантовой механике, приводит к тому, что в ряде случаев оказывается невозможным, в классическом смысле, одновременно характеризовать частицу ее положением в пространстве (координатами) и скоростью (или импульсом). Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и компоненты импульса . Неопределенности значений x и удовлетворяют соотношению:

.

(4.2.1)

Из (4.2.1) следует, что чем меньше неопределенность одной величины (x или ), тем больше неопределенность другой. Возможно, такое состояние, в котором одна их переменных имеет точное значение (), другая переменная при этом оказывается совершенно неопределенной ( – ее неопределенность равна бесконечности), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременного измерения координаты и импульса микрообъекта с любой наперед заданной точностью.

Соотношение, аналогичное (4.2.1), имеет место для y и , для z и , а также для других пар величин (в классической механике такие пары называются канонически сопряженными). Обозначив канонически сопряженные величины буквами A и B, можно записать:

.

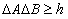(4.2.2)

Соотношение (4.2.2) называется соотношениемнеопределенностей для величин A и B. Это соотношение ввёл в 1927 году Вернер Гейзенберг.

Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга.

Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей:

.

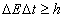(4.2.3)

Это соотношение означает, что определение энергии с точностью должно занять интервал времени, равный, по меньшей мере,

.

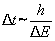Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличии у нее волновых свойств. Т.к. в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.

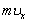Соотношение неопределенностей указывает, в какой мере возможно пользоваться понятиями классической механики применительно к микрочастицам, в частности с какой степенью точности можно говорить о траекториях микрочастиц. Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени. Подставив в (4.2.1) вместо произведение , получим соотношение:

.

(4.2.4)

Из этого соотношения следует, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости, следовательно тем с большей точностью можно применять к этой частице понятие траектории. Так, например, уже для пылинки массой кг и линейными размерами м, координата которой определена с точностью до 0,01 ее размеров ( м), неопределенность скорости, по (4.2.4),

т.е. не будет сказываться при всех скоростях, с которыми пылинка может двигаться.

Таким образом, для макроскопических тел их волновые свойства не играют никакой роли; координаты и скорости могут быть измерены достаточно точно. Это означает, что для описания движения макротел с абсолютной достоверностью можно пользоваться законами классической механики.

Предположим, что пучок электронов движется вдоль оси x со скоростью 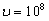м/с, определяемой с точностью до 0,01% ( м/с). Какова точность определения координаты электрона?

По формуле (4.2.4) получим:

.

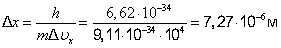Таким образом, положение электрона может быть определено с точностью до тысячных долей миллиметра. Такая точность достаточна, чтобы можно было говорить о движении электронов по определенной траектории иными словами, описывать их движения законами классической механики.

Применим соотношение неопределенностей к электрону, двигающемуся в атоме водорода. Допустим, что неопределенность координаты электрона м (порядка размеров самого атома), тогда, согласно (4.2.4),

.

Используя законы классической физики, можно показать, что при движении электрона вокруг ядра по круговой орбите радиуса приблизительно м его скорость м/с. Таким образом, неопределенность скорости в несколько раз больше самой скорости. Очевидно, что в данном случае нельзя говорить о движении электронов в атоме по определенной траектории. Иными словами, для описания движения электронов в атоме нельзя пользоваться законами классической физики.

Экспериментальное подтверждение идеи Луи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также противоречия ряда экспериментов с применяемыми в начале XX века теориями привели к новому этапу развития квантовой физики – созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств. Ее создание и развитие охватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20-х годов XX века и связано, прежде всего, с работами австрийского физика Э. Шредингера, немецкого физика В. Гейзенберга и английского физика П. Дирака.

Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Можно ли волны де Бройля истолковывать как волны вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно, хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.

Чтобы устранить эти трудности, немецкий физик М. Борн в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая . Эту величину называют также волновой функцией (или 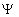-функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:

(4.3.1)

где , где – функция комплексно-сопряженная с Ψ.

Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волны де Бройля) определяет вероятность нахождения частицы в момент времени в области с координатами x и d x, y и d y, z и d z.

Итак, в квантовой механике состояние частицы описывается принципиально по-новому – с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых

.

(4.3.2)

Величина (квадрат модуля Ψ-функции) имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единице объема в окрестности точки, имеющей координаты x, y, z. Таким образом, физический смысл имеет не сама Ψ-функция, а квадрат ее модуля , которым определяется интенсивность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме о сложении вероятностей, равна:

.

Т.к. определяется как вероятность, то необходимо волновую функцию Ψ представить так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей:

(4.3.3)

где данный интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от до . Таким образом, условие нормировки говорит об объективном существовании частицы во времени и пространстве.

Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять ряду ограничительных условий. Функция Ψ, характеризующая вероятность обнаружения микрочастицы в элементе объема, должна быть:

· конечной (вероятность не может быть больше единицы);

· однозначной (вероятность не может быть неоднозначной величиной);

· непрерывной (вероятность не может меняться скачком).

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями , , … , 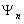то она может находиться в состоянии, описываемом линейной комбинацией этих функций:

,

где (n = 1, 2, 3…) – произвольные, вообще говоря, комплексные числа.

Сложение волновых функций (амплитуд вероятностей, определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.

Волновая функция Ψ является основной характеристикой состояния микрообъектов. Например, среднее расстояние электрона от ядра вычисляется по формуле

,

где вычисления проводятся, как и в случае (4.3.3).

Поиск по сайту: