 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Силы в механике:
Сила упругости – это сила, характеризующая интенсивность и направление реакции деформированного тела.
Сила всемирного тяготения – это сила, с которой все тела, вследствие обладания массой, притягиваются друг к другу.
Сила тяжести – сила притяжения к Земле тела, находящегося вблизи поверхности Земли.
Вес тела – это сила, с которой тело, вследствие притяжения к Земле, действует на опору или на подвес.
P = m*(g ± a)
Сила трения покоя – сила, характеризующая противодействие скольжению, возникающее на границе соприкосновения тел при их неподвижности относительно друг друга. Сила трения покоя максимальна в момент, непосредственно предшествующий началу движения тела.
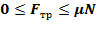
Сила трения скольжения – сила, характеризующая противодействие, возникающее на границе соприкосновения тел при их движении относительно друг друга.
Импульс тела — вектор, равный произведению массы этого тела на его скорость:
Импульсом системы называется векторная сумма импульсов тел, входящих в систему:
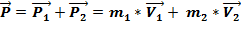
При взаимодействии элементов системы, между ними возникают равные и противоположные силы, которые принято называть внутренними:
(3-й закон Ньютона).
Это означает, что сумма импульсов элементов системы не изменяется в результате их внутреннего взаимодействия:
Сумма импульсов тел, образующих систему, называется её импульсом.
Результат, к которому мы пришли, можно сформулировать так: импульс системы двух тел не меняется в результате взаимодействия этих тел друг с другом.
Отсюда следует закон сохранения импульса:
Импульс замкнутой системы тел остаётся постоянным при любых взаимодействиях этих тел друг с другом.
Система называется замкнутой (или изолированной), если на элементы системы не действуют тела, не включённые в систему. В этом законе нужно обратить особое внимание на два положения:
Импульс системы — векторная величина. «Импульс сохраняется» — означает, что в замкнутой системе не меняется ни величина, ни направление вектора импульса.
Импульс замкнутой системы остаётся неизменным на фоне постоянно меняющихся импульсов элементов этой системы. Эти изменения носят характер передачи импульса (без потерь!) от одних тел системы в процессе взаимодействия — к другим.
Центр масс или система материальных точек – это воображаемая точка С, положение которой характеризует распределение массы этой системы, ее радиус вектора равен:
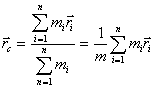
учитывая, что 
, a
т.е. импульс всей системы, то
т.е. импульс системы равен произведению массы системы на скорость ее центра масс. Если внешние силы отсутствуют, то система называется замкнутой. Для замкнутой системы суммарный импульс взаимодействующих тел сохраняется, т.е. не изменяется с течением времени:
и выражает закон сохранения импульса – это фундаментальный закон природы, он является следствием определенного свойства симметрии пространства – его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.
В физике работа неразрывно связана с изменением состояния тела или системы. Это изменение может выражаться самым различным образом: а) тело приобретает другую скорость, б) тело поднимается на другой уровень, в) тело деформируется, г) тело заряжается, д) тела намагничивается и т.д. Состояние механической системы (или тела) характеризуется одновременным заданием координат и скоростей всех точек системы (или тела) и может изменяться в процессе движения.
Процесс изменения характера движения тела происходит при его силовом взаимодействии с другими телами. Для количественного описания процесса вводят понятия силы и работы, совершаемой силой.
1. Если на тело действует постоянная сила F, и это приводит к перемещению S тела, то элементарной работой А постоянной силы называется скалярное произведение вектора силы F и вектора перемещения S:
Работа А - скаляр. Если угол 
- острый, то А положительная величина, и говорят, что сила совершает работу. Если угол - тупой, то А - отрицательная величина, и говорят, что работа совершается против действия силы. Если = 900, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.
2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 900), то работа А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом.
На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F i и ∆ r i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F i на своем малом участке (Рисунок 14):
где i = 1,2 … N - номер элементарного участка траектории.
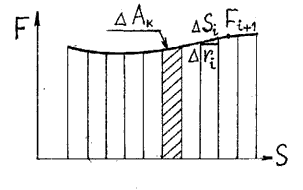
Рисунок 14 - График зависимости силы от пути.
На участке Si силу Fi можно считать постоянной, тогда элементарная работа Аi на участке S I равна:
Аi = Fi * Si и равна площади заштрихованной фигуры на рисунке 14.
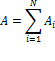
- это работа силы F на участке S, равна она численно площади фигуры, ограниченной кривой зависимости F(х) и осью Х.
Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.
Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.
Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными (потенциальными).
Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.
Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.
В физике консервативные силы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.
В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной (см. Фундаментальные взаимодействия). В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Для консервативных сил выполняются следующие равенства:
— работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело.
— работа консервативных сил по произвольному замкнутому контуру равна 0;
— ротор консервативных сил равен 0;
— консервативная сила является градиентом некой скалярной функции, называемой силовой. Эта функция равна потенциальной энергии взятой с обратным знаком. Соответственно, и связаны
соотношением:
Таким образом, потенциальная сила всегда направлена в сторону уменьшения потенциальной энергии.
Поиск по сайту: