Относительность времени

При движении на скоростях, близких к скорости света, возникает так называемый парадокс близнецов, к примеру, если один брат находится на земле, а другой в космосе и движется со скоростью, близкой к скорости света, то для брата, находящегося на земле время будет длиться гораздо медленнее, чем для того, который в космосе. Этот «парадокс» отчетливо можно объяснить с помощью преобразований Лоренца:
Когда скорость движения корабля близка к скорости света, то знаменатель становится достаточно мал, а значит время для человека, находящегося на земле будет длиться медленней, чем для человека в космосе на корабле.

Относительность длины.

Аналогично, при движении на скорости, близкой к скорости света происходит лоренцево сокращение длины.
Увидеть данную закономерность можно, если вычислить длину стержня в один и тот же момент времени, как разность конечной и начальной координаты по формулам Лоренца:
При стремлении скорости стержня к скорости света знаменатель дроби будет становиться <1, а значит и длина относительно инерциальной системы отсчета будет меньше.

МКТ

Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. Идеальным принято считать газ, если: а) между молекулами отсутствуют силы притяжения, т. е. молекулы ведут себя как абсолютно упругие тела;

б) газ очень разряжен, т. е. расстояние между молекулами намного больше размеров самих молекул;

в) тепловое равновесие по всему объему достигается мгновенно. Условия, необходимые для того, чтобы реальный газ обрел свойства идеального, осуществляются при соответствующем разряжении реального газа. Некоторые газы даже при комнатной температуре и атмосферном давлении слабо отличаются от идеальных. Основными параметрами идеального газа являются давление, объем и температура.

Одним из первых и важных успехов МКТ было качественное и количественное объяснение давления газа на стенки сосуда. Качественное объяснение заключается в том, что молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда.

На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа,

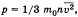
Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа
получим основное уравнение МКТ идеального газа в виде: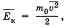

Идеальный газ - это простейшая физическая модель реального газа (т. е. газ, взаимодействием м/у молекулами которого можно пренебречь в силу чрезвычайной малости этой величины). Проще говоря, идеальным называется газ, в котором межмолекулярные силы взаимодействия отсутствуют.
Уравнение, связывающее р (давление газа), V (объём газа), Т (температуру газа) в какой-то конкретной данной системе, характеризующее её (системы) состояние, называется УРАВНЕНИЕМ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА.
PV / T = const, при m = const - уравнение Клапейрона
Для произвольной массы газа (т. е. в общем виде) это уравнение представляет собой УРАВНЕНИЕ МЕНДЕЛЕЕВА - КЛАПЕЙРОНА:
p*V = (m/M)*R*T,
или p*V = R*T (для 1 моля),
где р - давление; V - объём; m - масса; Т - абсолютная температура, К; m - масса газа, М - молярная масса газа; R =8,31 (Дж/(моль*К)

Температура - это величина, характеризующая состояние теплового равновесия (у тел, находящихся в состоянии теплового равновесия, температуры одинаковы и наоборот, тела с одинаковой температурой находятся в тепловом равновесии друг с другом).
Понятие абсолютной температура введено У. Томсоном (лордом Кельвином) в 1848 на основании теоремы КарнО

T = t + 273,15, К (t - температура в градусах по шкале Цельсия)
Абсолютная температура - мера средней кинетической энергии поступательного движения молекулы (это её молекулярно-кинетический смысл, т. к. с точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении и чем выше температура T, тем больше средняя кинетическая энергия хаотического движения молекул);
Согласно строгой формулировке второго начала термодинамики (аксиоматика Каратеодори), абсолютная температура вводится как интегрирующий делитель для бесконечно малого кол-ва теплоты dQ, полученного системой, обладающей внутренней энергией Е, в обратимом процессе.

АВОГАДРО ЗАКОН - один из основных законов идеальных газов: в равных объемах различных газов при одинаковой температуре и давлении содержится одинаковое число молекул. Открыт в 1811 году итал. физиком А.Авогадро(1776-1856).

БОЙЛЯ-МАРИОТТА ЗАКОН - один из законов идеального газа: для данной массы данного газа при постоянной температуре произведение давления на объем есть величина постоянная. Формула: p*V = const. Описывает изотермический процесс.

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ - один из основных законов термодинамики, согласно которому невозможен периодический процесс единственным результатом, которого является совершение работы, эквивалентной количеству теплоты, полученному от нагревателя. Другая формулировка: невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от менее нагретого тела к более нагретому. В.з.т. выражает стремление системы, состоящей из большого количества хаотически движущихся частиц, к самопроизвольному переходу из состояний менее вероятных в состояния более вероятные. Запрещает создание вечного двигателя второго рода.

ГЕЙ-ЛЮССАКА ЗАКОН - газовый закон: для данной массы данного газа при постоянном давлении отношение объема к абсолютной температуре есть величина постоянная ,где =1/273 К^-1 - температурный коэффициент объемного расширения.

ДАЛЬТОНА ЗАКОН - один из основных газовых законов: давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений этих газов.

ПАСКАЛЯ ЗАКОН - основной закон гидростатики:давление, производимое внешними силами на поверхность жидкости или газа, передается одинаково по всем направлениям.

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ - один из основных законов термодинамики, являющийся законом сохранения энергии для термодинамической системы: количество теплоты Q, сообщенное системе, расходуется на изменение внутренней энергии системы U и совершение системой работы A против внешних сил. Формула: Q= U+A. Лежит в основе работы тепловых машин.

ШАРЛЯ ЗАКОН - один из основных газовых законов: давление данной массы идеального газа при постоянном объеме прямо пропорционально температуре: где p₀ - давление при 0⁰С, =1/273,15 К^-1 - температурный коэффициент давления.

При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям делалось предположение, что внешние силы не действуют на молекулы газа, поэтому молекулы равномерно распределены по объему. Но молекулы любого газа находятся в потенциальном поле тяготения Земли. Сила тяжести, с одной стороны, и тепловое движение молекул — с другой, приводят газ к некоторому стационарному состоянию, при котором давление газа с высотой уменьшается.
Выведем закон изменения давления с высотой, предполагая при этом, что масса всех молекул одинакова, поле тяготения однородно и температура постоянна.

Рис.1

Если атмосферное давление на высоте h равно р (рис. 1), то на высоте h+dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой уменьшается). Разность давлений р и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м²:

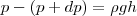
где ρ — плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом интервале плотность газа можно считать постоянной). Значит,
(1)
Зная уравнение состояния идеального газа pV=(m/M) RT (m — масса газа, М — молярная масса газа), находим, что

Подставив это выражение в (1), получим
или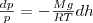
С изменением высоты от h₁ до h₂ давление изменяется от р₁ до р₂ (рис. 67), т. е.

или
(2)
Выражение (2) называется барометрической формулой. Она позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту: Так как высоты считаются относительно уровня моря, где давление считается нормальным, то выражение (2) может быть представлено в виде
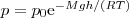(3)
где р — давление на высоте h.
Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на применении формулы (3). Из этой формулы следует, что чем тяжелее газ, тем давление с высотой убывает тем быстрее.
Барометрическую формулу (3) можно преобразовать, если воспользоваться формулой p=nkT:

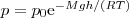
где n – концентрация молекул на высоте h, n₀ – то же, на высоте h=0. Так как M=m₀N_A (N_A – постоянная Авогадро, m₀ – масса одной молекулы), a R=kN_A, то
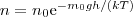(4)
где m₀gh=P — потенциальная энергия молекулы в поле тяготения, т. е.
(5)
Выражение (5) называется распределением Больцмана для внешнего потенциального поля. Из него видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.
Если частицы находятся в состоянии хаотического теплового движения и имеют одинаковую массу и, то распределение Больцмана (5) применимо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

При выводе основного уравнения молекулярно-кинетической теории полагалось, что молекулы имеют различные скорости. После многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Но из-за хаотического движения молекул все направления движения равновероятны, т. е. в любом направлении в среднем движется равное число молекул. Согласно молекулярно-кинетической теории, как бы ни изменялись при столкновениях скорости молекул, средняя квадратичная скорость молекул массой m0 в газе, который находится в состоянии равновесия при Т= const, остается неизменно и равной Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем статистическое распределение молекул по скоростям, подчиняющаяся вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом. При выводе закона распределения молекул по скоростям Максвелл сделал предположение, что газ состоит из огромного числа N тождественных молекул, которые находятся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют. Закон Максвелла описывается некоторой функцией f(ν), которая называется функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν)/N, скорости которых находятся в интервале от ν до ν +d ν, т. е. откуда 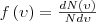Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределеня молекул идеального газа по скоростям: (1) Из (1) видно, что конкретный вид функции зависит от вида газа (от массы молекулы) и от параметра состояния (от температуры Т). График функции (1) приведен на рис. 1. Так как при возрастании ν множитель exp[–m0 ν 2/(2kT)] уменьшается быстрее, чем увеличивается множитель ν 2, то функция f(ν), начинаясь от нуля, достигает максимума при ν B, и затем асимптотически стремится к нулю. Кривая несимметрична относительно ν B. Рис.1 Относительное число молекул dN(ν)/N, со скоростями, лежащими в интервале от ν до ν +d ν, рассчитывается как площадь заштрихованной полоски на рис. 1. Площадь, которая ограничена кривой распределения и осью абсцисс, равна единице. Это значит, что функция f(ν) удовлетворяет условию нормировки Скорость, при которой максимальна функция распределения молекул идеального газа по скоростям, называется наиболее вероятной скоростью, значение которой можно найти продифференцировав выражение (1) (постоянные множители опускаем) по аргументу ν, при этом приравняв результат нулю и используя условие для максимума выражения f(ν): 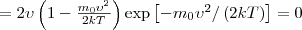Значения ν =0 и ν =∞ соответствуют минимумам выражения (1), а значение ν, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость ν B: (2) Из формулы (2) мы видим, что при возрастании температуры максимум функции распределения молекул по скоростям (рис. 2) движется вправо (при этом становится больше значение наиболее вероятной скорости). Однако площадь, которая ограничена кривой, не меняется, поэтому кривая распределения молекул по скоростям при повышении температуры будет растягиваться и понижаться. 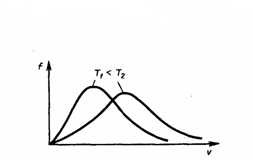Рис.2 Средняя скорость молекулы < ν > (средняя арифметическая скорость) определяется по формуле Подставляя сюда f(ν) и интегрируя, получаем (3) Скорости, которые характеризуют состояние газа: 1) наиболее вероятная 2) средняя 3) средняя квадратичная (рис. 1). Исходя из распределения молекул по скоростям (4) найдем распределение молекул газа по значениям кинетической энергии ε. С этой целью перейдем от переменной ν к переменной ε=m0v2/2. Подставив в (4) и , получим где dN(ε) — число молекул, которые имели кинетическую энергию поступательного движения, заключенную в интервале от ε до ε + dε. Значит, функция распределения молекул по энергиям теплового движения Средняя кинетическая энергия <ε> молекулы идеального газа т. е. получили результат, совпадающий с формулой о средней кинетической энергии движения одной молекулы идеального газа, выводимой из молекулярно-кинетической теории.

Механическое равновесие — состояние механической системы, при котором сумма всех сил, действующих на каждую её частицу, равна нулю и сумма моментов всех сил, приложенных к телу относительно любой произвольно взятой оси вращения, также равна нулю.

В состоянии равновесия тело находится в покое (вектор скорости равен нулю) в выбранной системе отсчета либо движется равномерно прямолинейно или вращается без касательного ускорения.

Поиск по сайту: