 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Распределение Больцмана. До сих пор рассматривалось поведение идеального газа, не подверженного воздействию внешних силовых полей
До сих пор рассматривалось поведение идеального газа, не подверженного воздействию внешних силовых полей. Из опыта хорошо известно, что при действии внешних сил равномерное распространение частиц в пространстве может нарушиться. Так под действием силы тяжести молекулы стремятся опуститься на дно сосуда. Интенсивное тепловое движение препятствует осаждению, и молекулы распространяются так, что их концентрация постепенно уменьшается по мере увеличения высоты.
Выведем закон изменения давления с высотой предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно p, то на высоте h + dh оно равно p + dp (при dh > 0, dp < 0, так как p уменьшается с увеличением h).
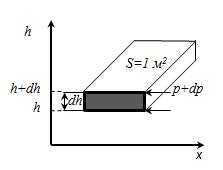 Разность давления на высотах h и h+dh мы можем определить как вес молекул воздуха заключённого в объёме с площадью основания равного 1 и высотой dh.
Разность давления на высотах h и h+dh мы можем определить как вес молекул воздуха заключённого в объёме с площадью основания равного 1 и высотой dh.
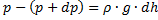
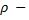 плотность на высоте h, и так как
плотность на высоте h, и так как 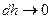 , то
, то 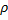 = const.
= const.
Тогда 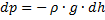 Из уравнения Менделеева-Клапейрона.
Из уравнения Менделеева-Клапейрона. 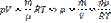
Тогда 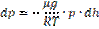 или
или 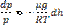 С изменением высоты от h1 до h2 давление изменяется от p1 до p2
С изменением высоты от h1 до h2 давление изменяется от p1 до p2 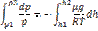
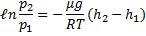
Пропотенцируем данное выражение (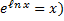
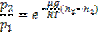
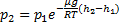
Барометрическая формула, показывает, как меняется давление с высотой
При 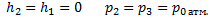
Тогда 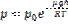 Т.к.
Т.к. 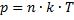 , а
, а 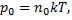 то
то 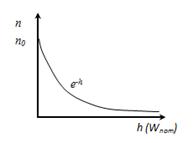
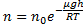 n - концентрация молекул на высоте h, n0 - концентрация молекул на высоте h =0. Т.к
n - концентрация молекул на высоте h, n0 - концентрация молекул на высоте h =0. Т.к 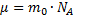
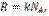 то
то 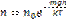
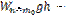 потенциальная энергия молекул в поле тяготения
потенциальная энергия молекул в поле тяготения 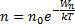
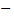 распределение Больцмана во внешнем потенциальном поле. Из него следует, что при T = const плотность газа больше там, где меньше потенциальная энергия молекул.
распределение Больцмана во внешнем потенциальном поле. Из него следует, что при T = const плотность газа больше там, где меньше потенциальная энергия молекул.
13. Равномерное распределение энергии по степеням свободы. Внутренняя энергия.
средняя энергия приходящаяся на одну степень свободы:
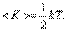
| (4.4.1) |
У одноатомной молекулы i = 3, тогда для одноатомных молекул
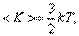
| (4.4.2) |
для двухатомных молекул
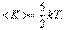
| (4.4.3) |
для трёхатомных молекул
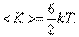
| (4.4.4) |
Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится
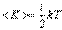
| (4.4.5) |
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.
Если система находится в состоянии термодинамического равновесия, при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы. На каждую поступательную iп и вращательную iвр степени свободы приходится энергия 1/2 kT. Для колебательной iкол, степени свободы она равна kT. Таким образом число степеней свободы i = iп + iвр + 2iкол
Внутренняя энергия термодинамическая функция состояния системы, ее энергия, определяемая внутренним состоянием. Внутренняя энергия складывается в основном из кинетической энергии движения частиц и энергии взаимодействия между ними (внутри- и межмолекулярной). На внутреннюю энергию влияет изменение внутреннего состояния системы под действием внешнего поля; во внутреннюю энергию входит, в частности, энергия, связанная с поляризацией диэлектрика во внешнем электрическом поле и намагничиванием парамагнетика во внешнем магнитном поле. Кинетическая энергия системы как целого и потенциальная энергия, обусловленная пространственным расположением системы, во внутреннюю энергию не включаются. В термодинамике определяется лишь изменение внутренней энергии в различных процессах. Поэтому внутреннюю энергию задают с точностью до некоторого постоянного слагаемого, зависящего от энергии, принятой за нуль отсчета.
Внутренняя энергия U как функция состояния вводится первым началом термодинамики, согласно которому разность между теплотой Q, переданной системе, и работой W, совершаемой системой, зависит только от начального и конечного состояний системы и не зависит от пути перехода, т.е. представляет изменение состояния Δ U
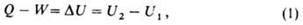
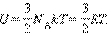
14. Среднее число столкнувшихся в секунду и средняя длина свободного пробега молекул.
Средние скорости молекул, газа очень велики - порядка сотен метров в секунду при обычных условиях. Однако процесс выравнивая неоднородности в газе вследствие молекулярного движения протекает весьма медленно. Это объясняется тем, что молекулы при перемещении испытывают соударения с другими молекулами. При каждом соударении скорость молекулы изменяется по величине и направлению. Вследствие этого, скорость, с которой молекула диффундирует из одной части газа в другую, значительно меньше средней скорости молекулярного движения. Для оценки скорости движения молекул вводится понятие средней длины свободного пробега. Таким образом, средняя дли свободного пробега 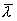 - это среднее расстояние, которое проходит молекула от столкновения до столкновения.
- это среднее расстояние, которое проходит молекула от столкновения до столкновения.
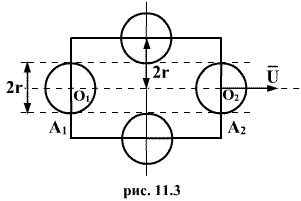
Молекулы, с которыми соударяется выбранная молекула, в первом приближении считаем неподвижными и принимаем их за сферические тела радиуса r. Пусть выбранная молекула движется вправо из положения 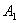 в положение
в положение 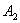 по прямой
по прямой 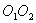 (рис.11.3). При своем движении она испытывает соударения с теми неподвижными молекулами, центры которых лежат не дальше чем 2r от траектории
(рис.11.3). При своем движении она испытывает соударения с теми неподвижными молекулами, центры которых лежат не дальше чем 2r от траектории 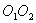 . Иными словами, движущаяся со средней скоростью молекула в течении одной секунды столкнется со всеми молекулами, центры которых находятся в объеме ограниченном цилиндром с радиусом 2r и длиной
. Иными словами, движущаяся со средней скоростью молекула в течении одной секунды столкнется со всеми молекулами, центры которых находятся в объеме ограниченном цилиндром с радиусом 2r и длиной 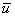 , т.е.
, т.е.
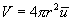 .
.
Если концентрация молекул n, то внутри рассмотренного цилиндра находится число молекул, равное
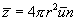
Это число 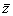 и определяет среднее число соударений за единицу времени.
и определяет среднее число соударений за единицу времени.
Предположение о том, что все молекулы, кроме одной, неподвижны, является, конечно не верным. В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости. Поэтому вместо среднеарифметической скорости 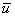 должны входить средняя относительная скорость молекул
должны входить средняя относительная скорость молекул 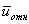 . Если скорости молекул распределены по закону Максвелла, то, как можно показать, средняя относительная скорость двух молекул однородного газа в
. Если скорости молекул распределены по закону Максвелла, то, как можно показать, средняя относительная скорость двух молекул однородного газа в 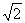 раз превышает
раз превышает 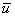 . Таким образом, среднее число соударений должно быть увеличено в
. Таким образом, среднее число соударений должно быть увеличено в 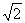 раз
раз
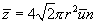
| (11.7) |
Средний путь, проходимый молекулой за единицу времени, численно равен 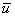 . Поэтому средняя длина свободного пробега равна
. Поэтому средняя длина свободного пробега равна 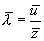 или
или
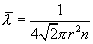
| (11.8) |
15. Кинетические процессы. Опытные законы явлений переноса. Вывод коэффицента диффузии.
Теплопроводность. Если в первой области газа средняя кинетическая энергия молекул больше, чем во второй, то вследствие постоянных столкновений молекул с течением времени происходит процесс выравнивания средних кинетических энергий молекул, т. е., выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье:
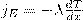 (1)
(1)
где jE — плотность теплового потока — величина, которая определяется энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х, λ — теплопроводность, — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус говорит о том, что во время теплопроводности энергия перемещается в направлении убывания температуры (поэтому знаки jE и – противоположны). Теплопроводность λ равна плотности теплового потока при градиенте температуры, равном единице.
Можно показать, что 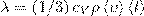 (2) где сV — удельная теплоемкость газа при постоянном объеме (количество теплоты, которое необходимо для нагревания 1 кг газа на 1 К при постоянном объеме), ρ — плотность газа, < ν > — средняя скорость теплового движения молекул, < l > — средняя длина свободного пробега.
(2) где сV — удельная теплоемкость газа при постоянном объеме (количество теплоты, которое необходимо для нагревания 1 кг газа на 1 К при постоянном объеме), ρ — плотность газа, < ν > — средняя скорость теплового движения молекул, < l > — средняя длина свободного пробега.
Диффузия. При происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия есть обмен масс частиц этих тел, при этом явление возникает и продолжается, пока существует градиент плотности. Во времена становления молекулярно-кинетической теории по вопросу явления диффузии возникли противоречия. Поскольку молекулы перемещаются в пространстве с огромными скоростями, то диффузия должна происходить очень быстро. Если же открыть в комнате крышку сосуда с пахучим веществом, то запах распространяется довольно медленно. Но здесь нет противоречия. При атмосферном давлении молекулы обладают малой длиной свободного пробега и, при столкновениях с другими молекулами, приемущественно «стоят» на месте.
16. Тепловые процессы. Работа и теплота.
ТЕПЛОВЫЕ ПРОЦЕССЫ В ТЕТРАДИ!
Поиск по сайту: