Формула преобразования скоростей

Достаточно продифференцировать 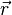в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.

Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так.

Рассмотрим преобразование произвольного сдвига начала отсчета на вектор ,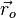

где радиус-вектор какого-то тела A в системе отсчета K обозначим за 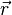, а в системе отсчета K' — за ,

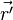подразумевая, как всегда в классической механике, что время 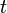в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени: .

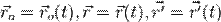Тогда в любой момент времени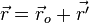

и в частности, учитывая ,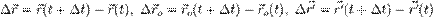

имеем: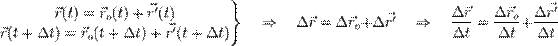

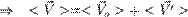
где: 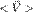— средняя скорость тела A относительно системы K;

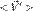— средняя скорость тела А относительно системы K';

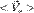— средняя скорость системы K' относительно системы K.

Если 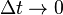то средние скорости совпадают с мгновенными:

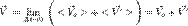или короче 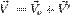— как для средних, так и для мгновенных скоростей (формула сложения скоростей).

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета.

· (Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга: ).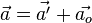

• 1)Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.
• 2)Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.

30. Преобразования Лоренца. Следствия преобразований Лоренца.

Поиск по сайту: