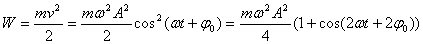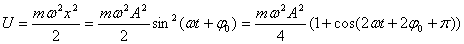Процесс Джоуля-Томсана сжижение газов

Процесс протекания газа по теплоизолированной трубе, в которой имеется пористая перегородка, называется дросилированием газа.

Эеффект Джоуля-Томсана состоит в умении температуры независить в результате медленного протекания газа под действием постоянного изменения давления через дроссель. Эффект Джоуля-Томсана свидетельствует о наличии в газе межмолекулярного взаимодействия.

Расширение газа в условиях его изоляции приводит к росту его потенциальной энергии за счёт увеличения расстояния между молекулами. Потенциальная энергия увеличивается за счёт кинетической в следствии температура газа увеличивается. В опыте Джоуля-Томсана определили, что остаётся неизменной величина эльтропия.

24. Колебания. Собственные колебания. Гармонический осциллятор.

Колебаниями называются движения или процессы, которые характеризуются определённой повторяемостью во времени.

Свободными (собственными) колебаниями называются колебания, которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния устойчивого равновесия; колебания, которые совершаются за счёт первоначально сообщённой энергии при последующем отсутствии внешних воздействий на колебательную систему.

Вынужденными называются колебания, возникающие в какой либо системе под влиянием переменного внешнего воздействия.

Период колебаний (T) - наименьший промежуток времени, по истечении которого система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный произвольно выбранный момент.

Частота колебаний – число полных колебаний, совершаемых в единицу времени. ν=1/T.

Амплитуда колебаний – это максимальное значение колеблющейся величины.

Фаза колебаний – это значение колеблющейся величины в произвольный момент времени (ω₀t+φ).

x = x_m cos (ωt + φ₀).

В классической механике, гармонический осциллятор — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы , пропорциональной смещению (согласно закону Гука): где — положительная константа, описывающая жёсткость системы.

Если — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постояной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

25. Математический маятник. Энергия гармонических конебаниях.

Математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести. Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

- груз на нити при малых отклонениях совершает гармонические колебания во времени t с периодом Т и амплитудой А.

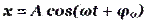- колебания происходят по закону синуса (начинаются от толчка груза).

-... или по закону косинуса (начинаются отведением груза в сторону).

- циклическая частота колебаний математического маятника.
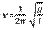- период колебаний математического маятника.
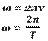- связь циклической частоты с частотой колебаний и периодом.

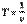- связь периода и частоты колебаний.
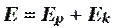Энергия колебаний пружинного маятника:
- Энергия колебаний - это сумма потенциальной энергии пружины и кинетической энергии груза.
Формулы потенциальной и кинетической энергий:

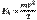
Кинетическая энергия тела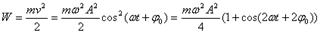

(Скорость тела v = ds/dt)

Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы: где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

Сравнивая формулы

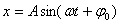
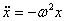
для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:

1. Полная механическая энергия тела не изменяется при колебаниях:
2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.
3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на p (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

В случае электрических колебаний энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие.

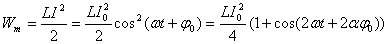
Сравнивая эти формулы, можно сделать следующие выводы:

Полная энергия в контуре остается неизменной: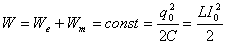

26. Ангармонический осциллятор. Линейный осциллятор с затуханием.

Ангармонический маятник. При больших амплитудах колебания маятника описываются нелинейным уравнением Угол отклонения входит в него как аргумент функции синуса. Поскольку при малых углах в случае малых колебаний переходит в уравнение гармонического осциллятора. Описываемые уравнением колебания являются ангармоническими: их период зависит от амплитуды. Приближенная формула для периода ангармонических колебаний маятника имеет вид где соответствует малым гармоническим колебаниям и дается формулой.

Гармонический осциллятор. Затухающие колебания и их характеристики.

Гармоническим осциллятором называется система, совершающая колебания, описыва­емые уравнением вида (142.1)

Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классичес­кой и квантовой физики. Примерами гармонического осциллятора являются пружин­ный, физический и математический маятники, колебательный контур.

Рассмотрим свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омичес­ких потерь и излучения электромагнитной энергии в электрических колебательных системах.

Закон затухания колебаний определяется свойствами колебательных систем. Обыч­но рассматривают линейные системы — идеализированные реальные системы, в кото­рых параметры, определяющие физические свойства системы, в ходе процесса не изменяются.

Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде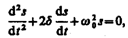

где s – колеблющаяся величина, описывающая тот или иной физический процесс, d=const — коэффициент затухания, w0 — циклическая частота свободных незатуха­ющих колебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис.).

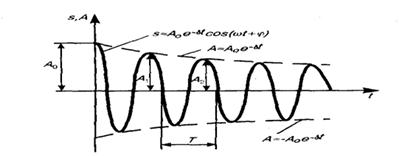
Свободные затухающие колебания пружинного маятника. Для пружинного маятника (см. § 142) массой т, совершающего малые колебания под действием упругой силы F= —kx, сила трения пропорциональна скорости, т. е.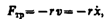

где r — коэффициент сопротивления; знак минус указывает на противоположные направления силы трения и скорости

2. Свободные затухающие колебания в электрическом колебательном контуре. Диф­ференциальное уравнение свободных затухающих колебаний заряда в контуре (при R¹0) имеет вид (см. (143.2))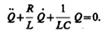

27. Вынужденные колебания осциллятора при периодическом воздействии(нет ответа). Резонанс.

РЕЗОНАНС (франц. resonance, от лат. resono - откликаюсь) - частотно-избирательный отклик колебат. системы на периодич. внеш. воздействие, при котором происходит резкое возрастание амплитуды стационарных колебаний. Резонанс в линейных системах с одной степенью свободы. Пример простейшего случая Р. представляют вынужденные колебания, возбуждаемые сторонним источником - гармонической эдс ~ E₀ cos pt с амплитудой Е₀ и частотой p - в колебательном контуре (рис. 1, а).

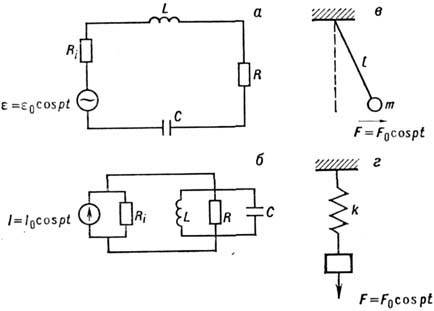
Рис. 1. Колебательные системы с одной степенью свободы: последовательный (а) и параллельный (б) колебательные контуры, математический маятник (в) и упругий осциллятор (г),

Амплитуда x и фаза f вынужденных колебаний заряда [ q(t) = x cos(pt +f)] определяются амплитудой и частотой внеш. силы:

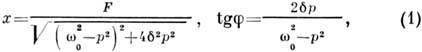
где F = E₀/L, d = (R + R_i)/2 L.

Зависимость амплитуды х стационарных вынужденных колебаний от частоты p вынуждающей силы при постоянной её амплитуде наз. резонансной кривой (рис. 2). В линейном колебат. контуре резонансные кривые, соответствующие различным F, подобны, а фазово-частотная характеристика f(p) не зависит от амплитуды силы.

Важной характеристикой резонансных свойств колебат. системы (осциллятора) является добротность Q,к-рая, по определению, равна умноженному на 2p отношению энергии, запасённой в системе, к энергии, рассеиваемой за период колебаний. При воздействии на резонансной частоте амплитуда вынужденных колебаний x в Q раз больше, чем в квазистатич. случае, при 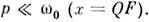Число периодов колебаний, в течение к-рых происходит установление стационарной амплитуды, также пропорц. Q. Наконец, добротность определяет частотную избирательность резонансных систем. Ширина полосы Р. Dw, в пределах к-рой амплитуда вынужденных колебаний спадает в 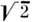раз от х, обратно пропорц. добротности: Dw = w₀/ Q = 2d.

28. Параметрические колебания и автоколебания. Сложение гармонических колебаний одинаковой частоты.

В некоторых «саморегулирующихся» системах незатухающие колебания могут поддерживаться постоянной внешней силой. Такие системы называются автоколебательными, а их поведение называется автоколебаниями. Классическим примером автоколебательной системы служат механические часы с маятником и гирями. Эти часы периодически "черпают" энергию при опускании гирь, подвешенных к цепочке, перекинутой через шестерню часового механизма. Важно отметить, что любая автоколебательная система нелинейна. На схеме это отражено наличием в системе обратной связи нелинейного ограничителя сигнала, управляющего ключом. Нелинейность системы проявляется в том, что при начальном нарастании амплитуды колебаний, порожденных флуктуациями, поступление энергии в систему за каждый последующий период колебаний увеличивается нелинейно, т.е. прирост поступающей энергии становится все меньше и меньше. Естественно, что амплитуда колебаний достигнет такой установившейся величины, при которой приток энергии и ее потери будут равны по величине.

Поиск по сайту: