АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Преобразования Лоренца. Пусть нам даны две системы отсчета k и k`

Читайте также:
  1. III ПРЕОБРАЗОВАНИЯ ПРИ ПОЛОВОМ СОЗРЕВАНИИ
  2. Базовые технологии преобразования информации
  3. Второе важное обстоятельство - преобразования Галилея меняют вид уравнений Максвелла
  4. Геометрические преобразования точек и отрезков. Однородные координаты
  5. Глава 14. Россия в конце XVII - первой четверти XVIII в. Петровские преобразования.
  6. Государственные преобразования.
  7. Движение заряда в магнитном поле. Сила Лоренца.
  8. Двумерные преобразования координат
  9. Декабристы: причины появления, разработка проектов преобразования России. Восстание 14 декабря и его итоги. Историческое значение.
  10. Доходы и уровень жизни. Кривая Лоренца.
  11. Доходы населения, виды доходов. Проблема неравенства доходов. Кривая Лоренца.
  12. й). 1924 - 32гг. - общедемократические преобразования.

Пусть нам даны две системы отсчета k и k`. В момент t = О обе эти системы координат совпадают. Пусть система k` (назовем ее подвижной) движется так, что ось х` скользит по оси х, ось у` параллельна оси у, скорость v - скорость движения этой системы координат (рис. 109).

Точка М имеет координаты в системе k - х, у, z, a в системе k` - х`, у`, z`.

Преобразования Галилея в классической механике имеют вид:

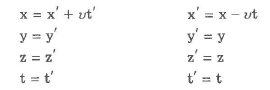
Преобразования координат, удовлетворяющие постулатам специальной теории относительности, называются преобразованиями Лоренца.

Впервые они (в несколько иной форме) были предложены Лоренцем для объяснения отрицательного эксперимента Майкельсона-Морли и для придания уравнениям Максвелла одинакового вида во всех инерциальных системах отсчета.

Эйнштейн вывел их независимо на основе своей теории относительности. Подчеркнем, что изменилась (по сравнению с преобразованием Галилея) не только формула преобразования координаты х, но и формула преобразований времени t. Из последней формулы непосредственно видно, как переплетены пространственная и временная координаты.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)