 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
В рамках доходного подхода наиболее часто используют два методаоценки
Метод дисконтирования денежных потоков. Данный метод предполагает построение ежегодного прогноза доходов (чаще всего чистого денежного потока). Для того, чтобы привести все будущие доходы к текущей стоимости, применяется ставка дисконтирования.
Метод капитализации прибыли. Применение метода предполагает преобразование годового дохода от данного бизнеса в стоимость бизнеса путем деления на ставку капитализации. Условие применения данного метода - неизменная величина годового дохода, планируемая в долгосрочной перспективе, или постоянные неизменные темпы роста.
Оценка облигаций с нулевым купоном.
Это самый простой случай. Поскольку денежные поступления по годам, за исключением последнего года, равны нулю, формула имеет вид:
 , (1)
, (1)
где Vt, – стоимость облигации с позиции инвестора (теоретическая стоимость); CF – сумма, выплачиваемая при погашении облигации; n – число лет, через которое произойдет погашение облигации; FM2(r, n) – дисконтирующий множитель из финансовой таблицы.
Оценка безотзывных облигаций с постоянным доходом.
Денежный поток в этом случае складывается из одинаковых по годам поступлений (С) и нарицательной стоимости облигации (М), выплачиваемой в момент погашения. Таким образом, формула трансформируется в выражение:
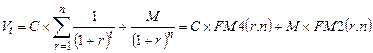 (2)
(2)
В экономически развитых странах весьма распространенными являются облигационные займы с полугодовой выплатой процентов. Такие займы более привлекательны, поскольку инвестор в этом случае в большей степени защищен от инфляции и, кроме того, имеет возможность получения дополнительного дохода от реинвестирования получаемых процентов.
Можно дать общую формулу для расчета внутренней стоимости облигации с выплатой процента каждые полгода:
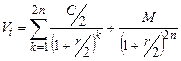 . (3)
. (3)
Привилегированные акции, как и бессрочные облигации, генерируют доход неопределенно долго, поэтому их текущая теоретическая стоимость определяется по формуле:
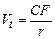 (4)
(4)
Таким образом, наиболее простым вариантом оценки привилегированной акции является отношение величины дивиденда к рыночной норме прибыли по акциям данного класса риска (например, ставке банковского процента по депозитам с поправкой на риск).
В некоторых странах привилегированные акции нередко эмитируются на условиях, позволяющих эмитенту выкупить их в определенный момент времени по соответствующей цене, называемой ценой выкупа (call price). В этом случае текущая теоретическая стоимость таких акций определяется по формуле (2), где М заменяется ценой выкупа Рс.
Поиск по сайту: