Принцип Гюйгенса - Френеля и некоторые его приложения

Волновая теория света победила лишь после того, как удалось построить удовлетворительную теорию дифракции и вывести из нее в качестве приближения «закон прямолинейного распространения света». Это сделал Френель (1816 г.). В основу своей теории дифракции он положил теорему Гюйгенса (1690 г.): каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, и волновым фронтом в любой последующий момент времени служит огибающая этих вторичных сферических волн (рис. 2.1 – построение Гюйгенса).

- фронт волны в некоторый момент времени ,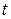

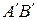- фронт волны в момент ( 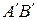- огибающая малых полусфер радиуса 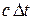, - скорость света).

Френель дополнил построение Гюйгенса утверждением: вторичные волныинтерферируют между собой. Таким образом, огибающая поверхность элементарных волн, введенная Гюйгенсом формально, приобрела физическое содержание как поверхность, где благодаря интерференции элементарных волн результирующая волна имеет заметную интенсивность. Это сочетание построения Гюйгенса с принципом интерференции называется принципом Гюйгенса - Френеля.

Вообразим некоторую (произвольную) замкнутую поверхность , охватывающую источник волн (рис. 2.2). Поверхность будем называть вспомогательной. Основная идея принципа Гюйгенса - Френеля состоит в следующем: колебание, создаваемое реальным источником 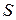в произвольной точке , может быть представлено как суперпозиция колебаний, которые создавали бы в этой точке фиктивные источники, непрерывно распределенные по поверхности . При этом величины, характеризующие фиктивные источники (амплитуда, фаза, вид диаграммы направленности), находящиеся на некотором элементе поверхности , зависят определенным образом от величин (амплитуды, фазы, направления распространения), характеризующих реальное колебание, создаваемое источником 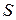в точках этого же элемента.

Принцип Гюйгенса - Френеля позволяет представить первичную волну вне поверхности как суперпозицию вторичных волн, излучаемых точками поверхности . Задача о распространении первичной волны в результате сводится к задаче о суперпозиции вторичных волн.

Оформим высказанные положения математически и сделаем следующие упрощающие задачу предположения: источник 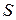испускает сферическую монохроматическую волну, исходная амплитуда которой равна , а произвольная поверхность совпадает с волновым фронтом от точечного источника, т. е. является сферой радиуса (рис. 2.3). Тогда амплитуда колебания, создаваемого в точке каким-либо произвольным элементом , выразится соотношением

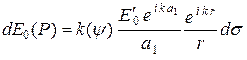, (2.1)

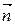в котором отброшена зависимость от времени (); - коэффициент наклона, описывающий изменение амплитуды вторичных волн в зависимости от направления, а - угол между нормалью и вектором , проведенным в точку . Угол часто называют углом дифракции. Следуя Френелю, предположим, что значение коэффициента наклона максимально в первоначальном направлении распространения света, т. е. при условии , быстро уменьшается с увеличением и равно нулю, когда

Замечание: введение такого коэффициента означает отсутствие обратной волны, направленной внутрь поверхности .

Суммарное возмущение в точке определится равенством

. (2.2)

Поиск по сайту: