Метод зон Френеля. Для того чтобы вычислить интеграл (2.2), воспользуемся так называемыми зонами Френеля

Для того чтобы вычислить интеграл (2.2), воспользуемся так называемыми зонами Френеля. Построим вокруг точки сферы с радиусами: (рис. 2.4), где , , и т. д. Сферы делят на целый ряд зон так, что волны от любых двух соседних зон приходят в точку в противофазе.

Покажем, прежде всего, что площади всех зон примерно одинаковы. Если - высота первого сегмента (рис. 2.4), то

(2.3)

.

Пренебрегая членом, пропорциональным , получаем:

. (2.4)

Отсюда площадь сферического сегмента, представляющего первую зону, равна

. (2.5)

Теперь сосчитаем таким же образом площадь двух первых зон:

, (2.6)

где - высота двух первых сегментов.

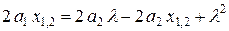и

, (2.7)

а площадь сферического сегмента, представляющего две первые зоны

. (2.8)

Сравнивая (2.8) и (2.5) видим, что с точностью до малых членов порядка площади первой и второй зон равны. Этот результат остается справедливым и для любых других зон.

Из тех же уравнений легко получить радиус -ой зоны Френеля :

. (2.9)

Займемся величиной элемента поверхности интегрирования . Из рис. 2.3 видно, что . Тогда

и

.

Элемент поверхности в сферических координатах записывается как . Подставляя найденное для выражение, имеем

. (2.10)

Теперь можно вычислить интеграл (2.2). Пусть 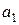и велики по сравнению с длиной волны; тогда можно предположить, что в пределах любой зоны величина коэффициента постоянна и в зоне равна . Тогда возмущение, создаваемое -ой зоной в точке , после интегрирования по азимутальному углу будет:

.

Справка:

,

,

Тогда

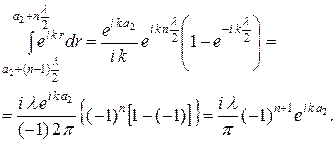
Окончательно получим:

. (2.11)

Следовательно, определение интегрального действия всех зон в точке сведется к суммированию знакопеременного ряда вида

. (2.12)

Сгруппируем члены ряда следующим образом:

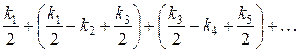
Величина каждого лишь немного отличается от величин соседних и 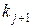. Легко доказать, что в зависимости от четности такая сумма приближенно будет равна

.

Это означает, что амплитуда суммарного колебания в точке равна полусумме (или полуразности) амплитуд колебаний, создаваемых в этой точке только первой и - ой зонами Френеля, т. е.

. (2.13)

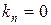Для последней зоны , видимой из точки , становится касательной к волновому фронту, т. е. , и для такого значения , по предположению, . Следовательно, , и (2.13) сводится к

. (2.14)

Обсуждение результатов. Выражение (2.14) показывает, что возмущение в точке равняется половине возмущения, обусловленного действием только первой зоны. Интенсивность излучения пропорциональна квадрату амплитуды колебаний. Значит, суммарная интенсивность в численно равна одной четвертой интенсивности, обусловленной первой зонойФренеля.

Оценим размеры первой зоны. Для ее площади была получена формула (2.5)

.

Так, например, при значениях 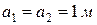и площадь зоны примерно равна 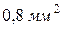. Число же зон Френеля приблизительно составляет

!

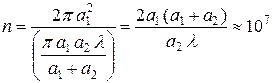Мы пришли к важнейшему заключению: в результате явления интерференции как бы уничтожается действие всех зон, кроме первой. Следовательно, распространение света от источника в точку действительно происходит так, как если бы световой поток шел внутри очень узкого канала вдоль , то есть прямолинейно.

2.4. Дифракция Френеля (понятие)

Если источник света и точка , в которой мы ищем распределение интенсивности, находятся на конечном расстоянии от экрана, то для определения интенсивности в точке играет роль лишь небольшой участок волновой поверхности, по которой происходит интегрирование в выражении (2.2). Этот участок лежит вблизи прямой, соединяющей источник с . В самом деле, поскольку отклонения от геометрической оптики слабы, то интенсивность света, приходящего в точку из различных точек волновой поверхности, очень быстро падает по мере удаления от указанной прямой. Дифракционные явления, в которых играют роль небольшие участки волновойповерхности, носят название дифракции Френеля.

2.5. Дифракция в параллельных лучах (дифракция Фраунгофера) (понятие – самостоятельно)

Поиск по сайту: