Понятие о дисперсии и разрешающей силе. Дисперсия и разрешающая сила дифракционной решетки

Исследуем, на какой угол 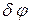будут разведены две волны 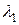и диспергирующим элементом. Обозначим разность ½ ½. Интересующая нас функция, называемая дисперсией, будет характеризоваться производной от угла по длине волны:

. (2.26)

При оценке дисперсии дифракционной решетки будем исходить из уравнения решетки 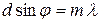. Дифференцируя, получаем

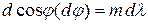или

. (2.27)

Для малых углов дифракции , и приближенно можно считать, что

. (2.28)

Следовательно, для получения высокой дисперсии период решетки 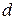должен быть малым или наблюдения должны вестись в высоких порядках (большое значение 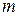). В последние годы практикуется использование решеток с очень большим числом штрихов на единицу длины (1200, 1800 и даже 2400 штрихов на 1 мм).

Замечание: при оценке дисперсии важно число штрихов на единицу длины 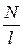, а не их общее число .

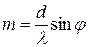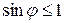Выгодно работать в высоких порядках дифракции, однако наибольший возможный порядок дифракции для данной решетки определяется длиной волны исследуемого излучения. И так как и , то 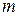не может превысить величины отношения 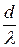. Например, для решетки, имеющей 1200 штрихов на 1 мм, период . При ее освещении красным светом (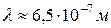) наблюдение можно вести лишь в первом порядке. Использование такой решетки даже в ближней инфракрасной области (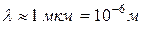) уже невозможно.

Разрешающая сила. Понятие дисперсии не позволяет полностью охарактеризовать способность спектрального прибора разлагать произвольное излучение на его составляющие. Для решения этой задачи важно не только развести излучение двух близких по длине волн на возможно больший угол, но и добиться того, чтобы каждая составляющая была достаточно узкой. В качестве примера на рис. 2.12 представлены две пары максимумов различной ширины, разведенных на один и тот же угол. В одном случае (рис. 2.12б) суммарная кривая позволяет наблюдать провал между максимумами, в другом (рис. 2.12а) - в излучении нельзя обнаружить две компоненты. Нужно как-то охарактеризовать аппаратную функцию, определяющую уширение линии падающего монохроматического излучения, создаваемое диспергирующим элементом. Такой характеристикой служит разрешающая сила. Для количественного введения этого понятия прежде всего необходимо условиться о критерии разрешения.

Критерий разрешения Рэлея: будем считать две линии разрешенными в том случае, когда максимум интенсивности для одной длины волны 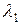совпадает с минимумом для другой 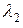. В этом случае (при равной интенсивности 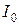исследуемых симметричных максимумов) глубина «провала» между горбами составляет примерно 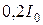(рис. 2.12б).

Примечание: любой критерий разрешения следует считать условным. Возможность разрешения двух близких спектральных линий лимитируется шумами в источнике и приемнике света, ограничивающими точность измерения полезного сигнала.

Разрешающей силой (иногда используется термин хроматическая разрешающая сила) называют отношени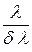е , где 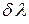- разность длин волн ½ 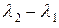½ между двумя максимумами, для которых выполняется критерий Рэлея, 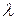- средняя длина волны, соответствующая центру провала в суммарном контуре.

Рассмотрим два максимума радиации, выделенных дифракционной решеткой с числом штрихов, равным . Пусть максимуму излучения 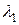соответствует угол дифракции 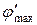, а максимуму излучения - угол 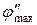. Условия возникновения главных максимумов 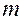-го порядка запишутся в виде:

, (2.29)

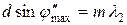. (2.30)

Условие же возникновения первого минимума излучения порядка 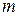для длины волны :

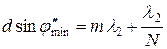. (2.31)

Для выполнения критерия Рэлея нужно положить равными углы 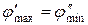. Откуда

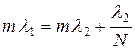
или

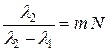. (2.32)

Левую часть равенства (2.32) можно с достаточной точностью принять равной отношению 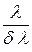; тогда для разрешающей силы дифракционной решетки получаем

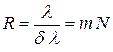. (2.33)

В отличие от дисперсии разрешающая сила определяется общим числом штрихов . Чем чаще расположены штрихи дифракционной решетки, тем больше угол, на который разводятся два близких по длине волны максимума излучения, а чем больше общее число штрихов, тем резче максимумы. Именно поэтому и стремятся изготовлять дифракционные решетки очень больших размеров. Рабочая область составляет 8 - 15 см, а у уникальных решеток она доходит до 20 см. Разрешающая сила современных дифракционных решеток достигает

Поиск по сайту: