 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение дифракционной решетки
При выполнении условия (2.23) 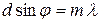 , называемого уравнением дифракционной решетки, интенсивность света, дифрагировавшего на системе из
, называемого уравнением дифракционной решетки, интенсивность света, дифрагировавшего на системе из  щелей, возрастает не в
щелей, возрастает не в  раз по сравнению с интенсивностью света, прошедшего через каждую щель, а в
раз по сравнению с интенсивностью света, прошедшего через каждую щель, а в  (!)раз. Это – прямое следствие интерференции дифрагировавших пучков, происходящей при дифракции на правильной структуре. Если бы
(!)раз. Это – прямое следствие интерференции дифрагировавших пучков, происходящей при дифракции на правильной структуре. Если бы  щелей располагались хаотически, то интерференционный член равнялся бы нулю, а суммарная интенсивность была бы просто пропорциональна числу щелей неправильной структуры.
щелей располагались хаотически, то интерференционный член равнялся бы нулю, а суммарная интенсивность была бы просто пропорциональна числу щелей неправильной структуры.
Максимумы, возникающие при выполнении (2.23) называются главными максимумами. Они появляются тогда, когда одновременно 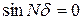 и
и 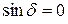 . Но между двумя главными максимумами должно возникнуть
. Но между двумя главными максимумами должно возникнуть  минимумов, где
минимумов, где 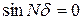 , но
, но  . Между этими минимумами должны находиться побочные, или дополнительные, максимумы, в которых интенсивность света при достаточно большом
. Между этими минимумами должны находиться побочные, или дополнительные, максимумы, в которых интенсивность света при достаточно большом  пренебрежимо мала по сравнению с интенсивностями главных максимумов.
пренебрежимо мала по сравнению с интенсивностями главных максимумов.
Для того чтобы лучше понять, как появляются главные и дополнительные максимумы интенсивности, запишем ряд значений величины  при последовательном их возрастании:
при последовательном их возрастании:
 0, p, 2p, ¼,
0, p, 2p, ¼,  p, Np,
p, Np,  p,
p, 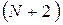 p, ¼,
p, ¼,  p, 2Np, ¼.
p, 2Np, ¼.
Здесь жирным шрифтом показаны главные максимумы, когда 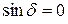 и
и 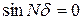 , а обычным - минимумы (
, а обычным - минимумы ( ).
).
Учтем теперь вклад в распределение интенсивности (2.22), который вносит каждая щель. Для этого необходимо исследовать, как ведет себя функция  при выполнении условия (2.23). По определению
при выполнении условия (2.23). По определению
 , но
, но  , откуда
, откуда
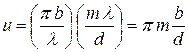 .
.
Тогда
 .
.
Отсюда интенсивность главного максимума порядка 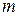
 . (2.25)
. (2.25)
Выводы:
а) 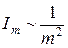 , т. е. с увеличением порядка дифракции
, т. е. с увеличением порядка дифракции 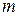 резко уменьшается интенсивность соответствующего главного максимума.
резко уменьшается интенсивность соответствующего главного максимума.
б) Интенсивность света в 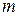 -ом максимуме существенно зависит от отношения
-ом максимуме существенно зависит от отношения  . Действительно, при условии
. Действительно, при условии  , где
, где 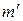 - целое число, выражение (2.25) обращается в нуль, т. к.
- целое число, выражение (2.25) обращается в нуль, т. к.  . Отсюда следует, что интенсивность света в этом главном максимуме равна нулю. Вспоминая, что условие возникновения минимума излучения при дифракции на одной щели имело вид
. Отсюда следует, что интенсивность света в этом главном максимуме равна нулю. Вспоминая, что условие возникновения минимума излучения при дифракции на одной щели имело вид  , замечаем, что рассматриваемый случай соответствует совпадению условий возникновения главного максимума дифракционной картины на
, замечаем, что рассматриваемый случай соответствует совпадению условий возникновения главного максимума дифракционной картины на  щелях и минимума дифракции на каждой щели (рис. 2.11). Например, при условии
щелях и минимума дифракции на каждой щели (рис. 2.11). Например, при условии  выпадает каждый четвертый максимум в дифракционной картине, что и показано на рис. 2.11.
выпадает каждый четвертый максимум в дифракционной картине, что и показано на рис. 2.11.
Итак, при дифракции плоской волны на правильной структуре из  щелей относительная интенсивность максимумов суммарной дифракционной картины обусловлена как зависимостью
щелей относительная интенсивность максимумов суммарной дифракционной картины обусловлена как зависимостью 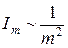 , так и отношением ширины щели
, так и отношением ширины щели  к постоянной решетки
к постоянной решетки 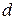 . Резкость максимумов определяется числом щелей
. Резкость максимумов определяется числом щелей  , а интенсивность каждого из них пропорциональна
, а интенсивность каждого из них пропорциональна  .
.
Поиск по сайту: