Дифракция Фраунгофера на прямоугольной щели. Влияние ширины щели

Тип дифракции, при котором рассматривается дифракционная картина, образованная параллельными лучами, получил название дифракции Фраунгофера. Принципиальная схема наблюдения дифракции плоских волн представлена на рис. 2.5.

Излучение точечного источника 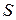превращается линзой в плоскую волну, которая проходит через какое-то отверстие в непрозрачном экране (щель, прямоугольник, круг и т. д.). Линза собирает в различных участках своей главной фокальной плоскости все лучи, прошедшие через отверстия, в том числе и лучи, отклонившиеся от первоначального направления в результате дифракции. Исследуя распределение освещенности в фокальной плоскости линзы , можно определить видность дифракционной картины.

Применение принципа Гюйгенса-Френеля в данном случае просто. Будем считать, что воображаемая поверхность совпадает с плоскостью непрозрачного экрана и целиком закрывает исследуемое отверстие. Если рассматривается наиболее простой случай - нормальное падение исходной волны на поверхность экрана, то дополнительная разность хода лучей от различных участков щели нацело определяется углом дифракции . Таким образом, метод расчета освещенности дифракционной картины сведется к учету интерференции между фиктивными элементарными источниками, заполняющими изучаемое отверстие в непрозрачном экране. В расчетах освещенности допустим когерентность освещения всего отверстия.

Рассмотрим излучение длинной и тонкой самосветящейся нити, которое преобразуется в плоскую волну, падающую нормально на щель ширины в непрозрачном экране. Образующие щели параллельны светящейся нити. Примем это направление за ось . Ось проведем в плоскости непрозрачного экрана перпендикулярно к образующим щели, а ось 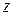- перпендикулярно к этой плоскости (рис. 2.6). В данном случае можно решать одномерную скалярную задачу.

Участок 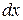посылает в направлении 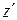, составляющим угол с осью 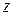, плоскую волну, направляющий косинус для которой равен . При записи амплитуды этой волны учтем, что вся щель в направлении посылает излучение с амплитудой 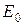. Следовательно, участок 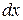щели, ширина которой , пошлет в направлении 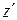волну с амплитудой 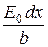, т. е.

,

откуда

(2.15)

Соотношение (2.15) легко преобразовать к симметричному виду, позволяющему применить формулу Эйлера:

. (2.16)

Амплитуда 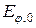этой волны равна

. (2.17)

Введем обозначение ; тогда

. (2.17а)

Интенсивность стационарной дифракционной картины 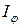будет

. (2.17б)

Исследуем эту функцию. Вспоминая, что , а условию соответствует , приходим к выводу, что интенсивность максимальна в центре дифракционной картины и . Это – главный максимум.

При некоторых углах, отличных от , будет наблюдаться полное исчезновение света. Это произойдет в случаях, когда , а . Отсюда получается условие возникновения минимумов интенсивности: , где или

, где . (2.18)

Первый минимум наблюдается под углом, удовлетворяющим условию . Далее станет ясным, что основная часть потока энергии сосредоточена в этих пределах изменения угла дифракции.

Минимумы (2.18) разделяют вторичные максимумы (значительно уступающие по величине главному), положение которых определяется корнями трансцендентного уравнения :

, и т. д. (2.19)

С увеличением угла дифракции быстро уменьшаются экстремальные значения функции . Если считать и обозначить интенсивность первого вторичного максимума через , а второго через , то получим .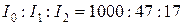

Таким образом, можно утверждать, что хотя основной световой поток сконцентрирован в пределах, определяемых значениями , некоторая часть его будет распространяться в направлении первых и даже вторых максимумов (примерно 5% и 2% энергии соответственно). Распределение интенсивности при дифракции плоской волны от щели - график функции - приведено на рис. 2.7.

Влияние ширины щели. Соотношение (2.18) позволяет исследовать зависимость ширины главного дифракционного максимума от линейных размеров отверстия (ширины щели ). С уменьшением расстояние минимумов от центра картины возрастает. Таким образом, чем уже щель, тем шире центральный максимум, и при условии он расплывается на всю полуплоскость (в этом случае , т. е. ), см. рис. 2.8. Дальнейшее уменьшение ширины щели не имеет смысла, т. к. при этом будет наблюдаться монотонное уменьшение интенсивности прошедшего света. В опытах по дифракции света обычно используют щели, ширина которых и, следовательно, угол дифракции , соответствующий первому минимуму, значительно меньше .

Напротив, при увеличении ширины щели положение первых минимумов придвигается все ближе и ближе к центру картины, так что центральный максимум становится все резче и резче. При этом относительная интенсивность максимума остается неизменной; абсолютная же величина его возрастает, ибо возрастает энергия, проходящая через уширенную щель (см. (2.17б)). При очень широкой щели по сравнению с длиной волны мы получаем в центре резкое изображение источника.

Поиск по сайту: