 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Динамический метод оценки эффективности инвестиционных проектов
По своей экономической сущности инвестиции – это, с одной стороны, затраты на приобретение имущества или других активов с целью получения доходов, с другой – активы, приобретенные с целью получения прибыли [1,4,9,11]. Процесс инвестирования можно определить как обмен удовлетворения сегодняшней потребности на ожидание удовлетворения других потребностей в будущем с помощью инвестиционных затрат (рис.1.3.1).
 |
Рис. 1.3.1. Экономическая сущность инвестиций
Реальные инвестиции – это финансовые вложения в конкретные долгосрочные проекты, включающие сумму средств, требующих для строительства и оснащения оборудованием инвестируемых объектов, расходов на подготовку этого строительства и дополнительные оборотные средства, необходимые для начала нормальной работы объекта. Такие затраты складываются из следующих составляющих: проведение проектно-конструкторских работ; затраты на пользование земельным участком; издержки на подготовку строительной площадки; на приобретение машин и оборудования и пусконаладочные работы; на строительство зданий и инженерных сооружений; на прирост оборотного капитала; на непредвиденные расходы.
Реальные инвестиции увеличивают производственные мощности каждого предприятия.
Инвестиционным является такой проект, если в результате принятия решения о нем изменяются структура, состав и объем активов предприятия или компании, а отдача от решения ожидается в течение относительно длительного времени. При этом требуются, как правило, существенные текущие затраты.
Для принятия решения о долгосрочном вложении капитала необходимо располагать информацией, которая в определенной мере может подтвердить два основных предположения: первое, что вложенные средства будут полностью возмещены; второе, что прибыль, полученная от инвестиционной операции, будет достаточно велика, чтобы компенсировать временный отказ от использования средств, а также риск, который возникает вследствие неопределенности конечного результата.
Для реализации инвестиционных проектов в планируемом периоде необходимо формирование финансовых затрат как в планируемом, так и в последующих периодах. Совокупность таких финансовых затрат называется текущим инвестиционным бюджетом организации, а инвестиционный проект трансформируется в инвестиционный план.
Чистая приведенная стоимость (Net Present Value,NPV) проекта определяется по формуле
 (1.3.1)
(1.3.1)
где r – норма дисконта; n – число периодов реализации проекта; СF1 – свободный денежный поток от операций проекта в периоде t1; CIF1 – суммарные поступления от проекта в периоде t; COF1 – суммарные выплаты по проекту в периоде t.
 |
Если рассчитанная таким образом чистая современная стоимость потока платежей имеет положительный знак (NPV > 0), это означает, что в течение своей экономической жизни проект возместит первоначальные затраты IС0, обеспечит получение прибыли согласно требуемой норме доходности r, а также ее некоторую дополнительную величину, равную NPV. Другими словами, NPV является мерой добавочной, или вновь созданной, стоимости проекта, которую фирма получит в случае его успешной реализации.
Отрицательная величина NPV показывает, что заданная норма доходности не обеспечивается и проект является убыточным, т. е. не создает новой стоимости. При NPV = 0 проект только окупает произведенные затраты, но не приносит доход.
Пример 1.3.1 определения экономической эффективности инвестиционного проекта.Для реализации проекта необходимо вложить средства в приобретение нового оборудования, стоимость которого вместе с доставкой и установкой составит 100 000 руб. Ожидается, что внедрение оборудования обеспечит получение на протяжении 6 лет чистые доходы в 25 000 руб., 30 000 руб., 35 000 руб., 40 000 руб., 45 000 руб. и 50 000 руб. соответственно. Норма дисконта равна 10%.
Таблица П.1.3.1. Расчет NPV проекта, ед.
| T | IC0 | CFt | (1 + r) t | PVt | NPV |
| -100 000,00 | 1,0000 | -100 000,00 | -100 000,00 | ||
| 25 000,00 | 1,1000 | 22 727,27 | - 77 272,73 | ||
| 30 000,00 | 1,2100 | 24 793,39 | -52 479,34 | ||
| 35 000,00 | 1,3310 | 26 926,02 | -26 183,32 | ||
| 40 000,00 | 1,5041 | 27 320,54 | 1137,22 | ||
| 45 000,00 | 1,6105 | 27 941,50 | 29 078,68 | ||
| 50 000,00 | 1,7716 | 28 223,70 | 57,302,37 | ||
| Итого | -100 000,00 | 225 000,00 | 157 302,37 | 57 302,37 |
Как следует из таблицы, при условии правильной оценки денежного потока проект обеспечивает возмещение произведенных затрат (примерно к концу 4-го года) и получение 10% чистой прибыли, а также дополнительной (сверх установленной нормы) прибыли, равной величине NPV(57 302,37). Показатель NPV должным образом отражает соотношение между притоками и оттоками денежных средств в течение определенного периода времени, а также дает представление как о возмещении произведенных затрат, так и о достижении заданной нормы доходности вложения средств.
Являясь абсолютным показателем, NPV обладает свойством аддитивности, т.е. NPV различных проектов можно суммировать:
NPV(A, B,С) = NPV(A) + NPV(B) + NPV(С). (1.3.2)
К числу других важнейших свойств этого критерия следует отнести реалистичные предположения о ставке реинвестирования поступающих средств. В методе NPV неявно предполагается, что средства, поступающие от реализации проекта, реинвестируются по заданной норме дисконта r, под которой обычно понимают средневзвешенную стоимость капитала для предприятия. Наконец, критерий NPV позволяет судить об изменении стоимости предприятия в результате осуществления проекта, т. е. об успешности реализации одной из основных целей финансового менеджмента. Вместе с тем применение показателя NPV в качестве сравнительной оценки не всегда удобно на практике, так как абсолютные величины трудно сопоставлять.
Пример 1.3.2. Имеются два проекта.Принятая норма дисконта составляет 10%. Оценки денежных потоков и NPV, приведенные в табл. П1.3.2., показывают, что чистая современная стоимость обоих проектов составляет 5000 тыс.руб., т.е. формально нельзя однозначно определить лучший вариант.
Таблица П1.3.2. Условия реализации проектов, тыс. руб.
| Проект | ICo | CFt | PV | NPV |
| X | -10 00 | 16 500 | 15 000 | |
| Y | -100 000 | 115 000 | 105 000 |
В этой связи широкое применение в финансовом менеджменте получили относительные критерии, такие как внутренняя норма доходности и индекс рентабельности.
Внутренняя норма доходности (Internal Rate of Return — IRR) является наиболее широко используемым критерием эффективности инвестиций. Под внутренней нормой доходности понимают процентную ставку в коэффициентедисконтирования, при которой чистая современная стоимость денежного потока инвестиционного проекта NPV равна нулю.
Внутренняя норма доходности определяется решением уравнения
 (1.3.3)
(1.3.3)
Это уравнение решается относительно IRR каким-либо итерационным методом. Нетрудно заметить, что при NPV = 0 чистые приведенные стоимости поступлений и выплат проекта равны между собой. Следовательно, проект окупается.
В общем случае, чем выше величина IRR, тем больше экономическая эффективность инвестиций. В процессе принятия решения величина IRR сравнивается с некоторой барьерной ставкой r (hurdle rate),отражающей требуемую инвесторами доходность либо стоимость капитала для фирмы. При этом если IRR > r, проект обеспечивает положительную чистую доходность, равную IRR - r. Если IRR < r, затраты превышают доходы, и проект будет убыточным.

Показатель IRR имеет несколько полезных интерпретаций:
во-первых, он может рассматриваться в качестве максимальной ставки платы за привлекаемые источники финансирования проекта, при которой последний остается безубыточным;
во-вторых, значение IRR может трактоваться как нижний уровень прибыльности инвестиционных затрат. Если он превышает среднюю стоимость капитала или норму доходности в данной отрасли, проект может быть рекомендован к осуществлению;
в-третьих, внутренняя норма прибыли может трактоваться как предельный уровень окупаемости инвестиций, что может быть критерием целесообразности дополнительных капиталовложений в проект.
Расчет IRR вручную может оказаться трудоемким. Однако все современные программные средства инвестиционного анализа позволяют быстро и эффективно определить этот показатель. В частности, табличные процессоры типа MS EXCEL содержат специальные встроенные функции для его автоматического вычисления.
Для примера П1.3.1. расчетное значение IRR оказалось равным 26%. Поскольку полученный результат превышает норму дисконта (10%), критерий IRR также рекомендует принять проект. При этом эффективность данной операции составит 26% - 10% = 16%.
Показатель IRR, рассчитываемый в процентах, является более удобным для применения в анализе, чем показатель NPV, поскольку относительные величины легче поддаются интерпретации. Например, эффективность проекта с IRR = 26% очевидна, если стоимость привлечения капитала для его реализации равна 10%.
Критерий внутренней нормы доходности несет в себе также информацию о приблизительной величине «предела безопасности», или риска для проекта. Например, при оценке денежного потока возникла ошибка, и IRR проекта окажется равной 20%. Тогда при прежней ставке дисконтирования в 10% проект все равно обеспечит получение дохода. В случае же повышения стоимости капитала до 24% при IRR= 26% остается слишком малый предел безопасности на случай ошибки. Возможно, такой проект должен быть сразу отвергнут и проведение дальнейшего анализа не потребуется.
В отличие от NPV, критерий внутренней нормы доходности неявно предполагает реинвестирование получаемых доходов по ставке IRR. Если стоимость финансирования проекта равна 10%, а полученное значение IRR = 26%, то поступления от его реализации должны быть реинвестированы по ставке 26%, т. е. в 2,6 раза превышающей цену капитала! Очевидно, что это вряд ли осуществимо в реальной практике.
Для преодоления указанного недостатка был разработан прои зводный от IRR критерий, получивший название модифицированной нормы доходности (Modified Internal Rate of Return - MIRR), определяемый по формуле
 (1.3.4.)
(1.3.4.)
Рассчитываемый по формуле (1.16) критерий MIRR предполагает, что поступления от проекта реинвестируются по ставке г, в качестве которой обычно используется средняя цена капитала для предприятия. В этом случае формула (1.16) примет вид
 (1.3.5)
(1.3.5)
где j – предполагаемая ставка реинвестирования.
В целом MIRR — далеко не идеальный метод, но он позволяет установить более реалистичные ставки реинвестирования и подсчитать реальный годовой эквивалент дохода.
Однако в случае чередования притоков и оттоков денежных средств для инвестиционного проекта могут существовать несколько значений IRR. Объяснение этого факта следует из соотношения (1.3.1), в котором IRR является корнем функции NPV = f(r) =0 и в общем случае задается полиномом n-й степени, где и — число периодов реализации проекта. Согласно известному правилу Декарта полином n-й степени может иметь столько корней, сколько раз меняет знак заданная им функция. Таким образом, уравнение NPV = f(r) = 0 имеет столько корней, сколько раз меняется знак потока платежей.
Пример П1.3.3. Фирма рассматривает возможность реализации проекта, генерирующего денежный поток, представленный в табл.П.1.3.3. Определим эффективность проекта, если норма дисконта равна 10%.
Таблица П1.3.3. Поток платежей проекта, ед.
| Период | t0 | t1 | T2 |
| CF, | -1600 | 10 000 | -10 000 |
Расчеты показывают, что критерий NPV= —773,55тыс.руб. рекомендуется отклонить проект. Определим величину IRR из выражения
-10 000/(1 + IRR)2 + 10 000/(1 + IRR) - 1600 = 0.
Умножив это уравнения на (1 + IRR)2, имеем
1600(1 + IRR)2 + 10 000(1 + IRR) - 10 000 = 0.
Нетрудно заметить, что полученное соотношение является квадратным уравнением и имеет два корня:
 , откуда IRR1 = 25% и IRR2 = 400%.
, откуда IRR1 = 25% и IRR2 = 400%.
График зависимости NPV от нормы дисконта r для рассматриваемого примера приведен на рис. 1.3.2.
Принятие решений в подобных случаях представляет определенную проблему. Наиболее простое решение в такой ситуации — руководствоваться наименьшим значением среди всех полученных IRR либо изменение ставки дисконтирования - может оказаться неприемлемым на практике. В более сложных ситуациях уравнение (1.3.1) может вообще не иметь решения либо действительных корней. Критерий IRR может приводить к некорректным выводам при анализе взаимоисключающих проектов с различными исходными условиями (первоначальными инвестициями, сроками экономической жизни и др.).

|
Рис. 1.3.2. Множественные значения IRR.
Аналогично, если проекты требуют одинаковые объемы инвестиций, но приток денежных средств по одному из них осуществляется быстрее, фирма имеет большие возможности для реинвестирования. При этом важнейшее значение имеет цена капитала (ставка дисконтирования), по которой притоки средств могут быть реинвестированы. Если цена капитала постоянна, следует выбирать проект с большей NPV. В примере П1.3.4. таким проектом является «Б», который имеет большую NPV и, следовательно, увеличивает богатство собственников в большей степени.
Пример П1.3.4. Предположим, что рассмотрению подлежат два взаимоисключающих проекта «Б» и «М». Принятая норма дисконта составляет 15%. Соответствующие оценки денежных потоков и расчет критериев эффективности приведены в табл. П1.3.4.
Таблица П1.3.4. Условия реализации проектов, тыс. руб.
| Период | Проект «М» | Проект «Б» | Проект «Д» |
| -20 000 | -130 000 | -110 000 | |
| 15 000 | 80 000 | 65 000 | |
| 15 000 | 60 000, | 45 000 | |
| 15 000 | 80 000 | 65 000 | |
| NPV | 14 248,38 | 37 535,14 | 23 236,76 |
| IRR, % |
Как следует из полученных результатов, при заданной ставке дисконтирования критерий NPV рекомендует принять проект «Б», в то время как критерий IRR — проект «М». На рис. 1.3.2приведены графики зависимости NPV проектов «Б» и «М» от ставки дисконтирования r. Как следует из рис. 1.3.3, проект «Б» имеет большую NPV пpименьших значениях r, и при r = 28% (точка пересечения графиков) уже имеет меньшую NPV. Отметим также, что с ростом r величина NPV проекта «Б» убывает сильнее. Другими словами, проект «Б» более чувствителен к росту ставки дисконтирования, чем проект «М». В данном примере выбор проекта «М» вместо «Б» означает, что в момент времени t=0 фирма будет располагать дополнительными ресурсами для инвестирования в объеме 110 000 тыс. руб.. (см. гр. 3 табл. П1. 3. 4).

|
Рис. 1.3.3. Графики зависимости NPV проектов от ставки r.
Для подтверждения корректности этого правила рассмотрим гипотетический дополнительный проект «Д» = «Б» - «М» (см. гр. 3 табл. П1.3.4). Его NPVД = NPVБ - NPVM = 23286,76 > 0, следовательно, по формальным признакам его следует принять. Таким образом, принимая проект «Б», фирма тем самым реализует как бы два проекта «М» и «Д». При этом оба проекта имеют положительные NPV и увеличивают стоимость фирмы.
В то же время принятие проекта «М» автоматически ведет к отказу от реализации дополнительного гипотетического проекта «Д». Другими словами, в данных условиях принятие проекта «М» ведет к потере дополнительной стоимости в 23 286,76 тыс. руб..
Отметим, что значение r = 28%, при котором значения NPV проектов «Б» и «М» одинаковы, представляет собой IRR гипотетического проекта «Д». При ставке дисконтирования r - 28% противоречия между критериями не возникают, и проект «М» будет предпочтительнее.
Таким образом, корректное применение показателя IRR требует тщательного изучения и глубокого понимания теоретических предпосылок, лежащих в его основе.
Еще одним популярным относительным критерием оценки эффективности инвестиций является индекс рентабельности(Profitability Index — PI), показывающий, сколько единиц приведенной величины денежных поступлений проекта приходится на единицу предполагаемых выплат. Для расчета показателя используется формула
 (1.3.6)
(1.3.6)
Если величина критерия Р1> 1, то денежные поступления от потока проекта превышают необходимые затраты, обеспечивая тем самым наличие положительной величины NPV. При PI = 1 величина NPV= 0 и инвестиции не приносят дохода. В случае, если PI < 1, проект не покрывает связанных с ним издержек и его следует отклонить.
|
Применение показателя РI часто бывает полезным, когда существует возможность финансирования нескольких проектов, но инвестиционный бюджет фирмы ограничен. Как и критерий IRR, индекс рентабельности PI косвенно несет в себе информацию о риске проекта, т. е. о его устойчивости к изменению исходных параметров.
Следует отметить, что индекс рентабельности не всегда обеспечивает однозначную оценку эффективности инвестиций, и проект с наиболее высоким PI может не соответствовать проекту с наиболее высокой NPV. В частности, использование индекса рентабельности может привести к ошибочным результатам при оценке взаимоисключающих проектов.
Пример П1.3.5. Предусматривается возможность участия в финансировании одного из двух взаимоисключающих проектов, предполагаемые условия реализации которых приведены в табл. П1.3.5. Принятая норма дисконта для проектов одинакова и равна 10%. Необходимо выбрать наиболее эффективный проект инвестиций.
Таблица П1.3.5. Потоки платежей проектов, тыс.руб.
| Проект | IQ0 | CF1 | CF2 | PV | NPV |
| -100,00 | 200,00 | 250,00 | 388,43 | 288,43 | |
| -10000,00 000,00 | 15 000,00 | 25 000,00 | 34 297,52 | 24 297,52 |
Определим индексы рентабельности для проектов 1 и 2.
РI1 = 388,43 / 100,00 = 3,88,
PI2 = 34 927,52 / 10 000,00 = 3,43.
Заметим, что при наличии у фирмы соответствующих средств выбор проекта 2более предпочтителен, так как он генерирует большую NPV. Однако индекс рентабельности «отдает» предпочтение проекту 1.
Обычно расчет индекса рентабельности выполняют в дополнение к расчету NPV cцелью отбора проектов, порождающих максимальную чистую приведенную стоимость на единицу затрат.
Заключительным из традиционных критериев эффективности является дисконтированный срок окупаемости. Дисконтированный срок окупаемости {Discounted Payback Period — DPP) представляет собой число периодов (как правило — лет), в течение которых будут возмещены вложенные инвестиции. Этот критерий характеризует ликвидность и косвенно — риск проекта. Его можно рассматривать в качестве точки безубыточности, т. е. момента времени, к которому окупаются все затраты по финансированию проекта с учетом заданной нормы доходности (стоимости капитала) r. Данный показатель определяется путем решения относительно t уравнения
 (1.3.7)
(1.3.7)
Таким образом, в математическом отношении дисконтированный срок окупаемости представляет собой период времени, когда NPV проекта становится равной 0 (см. рис. 1.3.3). В общем случае, чем меньше срок окупаемости, тем более эффективным является проект. На практике величину DPP сравнивают с некоторым заданным периодом времени п.
|
Расчет дисконтированного срока окупаемости вручную представляет определенные трудности. Его точное значение может быть определено решением уравнения (1.19) каким-либо из итерационных методов. На практике, поскольку методика определения DPP базируется на дисконтировании потоков платежей, для его расчета используется более простой подход.
Пример П1.3.6. Определить дисконтированный срок окупаемости для проекта из примера П1.3.1. Как следует из табл. П1.3.1 с расчетом дисконтированных потоков платежей, срок окупаемости проекта лежит между периодами 3 и 4. При этом невозмещенная сумма инвестиционных затрат в периоде 3 (см. гр. 5 табл. П1.3.1) равна - 26 183,32 тыс. руб., а величина дисконтированных денежных поступлений в следующем году (гр. 4) положительна и составляет 27 320,54 тыс. руб. Отсюда точное значение показателя DPP может быть определено как DPP = 3 + (26 183,32 / 27 320,54) = 3,96 года.
График зависимости величины NPV от временного периода t для рассматриваемого примера приведен на рис. 1.3.4.
К достоинствам показателя DPP следует отнести простоту интерпретации, а также то обстоятельство, что он является единственной формальной характеристикой ликвидности проекта. Нетрудно заметить, что ориентация на данный критерий стимулирует принятие краткосрочных проектов, что положительно отражается на ликвидности фирмы. Иными словами, срок окупаемости «поощряет» такие инвестиционные проекты, которые способны быстро высвободить и сгенерировать денежные средства для иных потребностей, что особенно важно для небольших предприятий.

Рис. 1.3.4. Зависимость NPV от периода времени t
С другой стороны, более отдаленные по времени получения денежные потоки характеризуются большой неопределенностью. Таким образом, критерий DPP, по сути, изначально ориентирует менеджера на принятие менее рисковых проектов. В практическом аспекте инвестиции, дающие быструю отдачу и приносящие прибыль после срока окупаемости, как правило, будут иметь положительную NPV. Кроме того, критерий DPP автоматически отклоняет проекты с NPV< 0. Наконец, концепция срока окупаемости проста для понимания на интуитивном уровне.
Наиболее серьезным недостатком DPP является игнорирование денежных потоков, возникающих после периода окупаемости. Таким образом, долгосрочные проекты, генерирующие в конечном итоге положительные значения NPV, могут быть отклонены. С другой стороны, принятые согласно этому критерию проекты могут иметь меньшие NPV, чем отклоненные, или даже отрицательные значения. Из изложенного следует, что его использование не позволяет принимать решения, ориентированные на максимизацию стоимости фирмы.
Пример П1.3.7. Оцениваются несколько инвестиционных проектов, затраты и дисконтированные потоки платежей по которым представлены в табл. П1.3.6. Инвестиционная политика фирмы предусматривает использование показателя DPP в качестве критерия отбора проектов, контрольный срок окупаемости п составляет не более 3 лет. Определим наиболее привлекательный вариант инвестиций.
Как следует из приведенной таблицы, наиболее привлекательным проектом по критерию DPP при п - 3 года является проект «Д». Однако при этом игнорируется существенный отток денежных средств, возникающий в периоде 4, который обеспечивает в результате отрицательное значение NPV. Проект «В» имеет два срока окупаемости и нулевую NPV. Проект «Б» является наиболее привлекательным по критерию NPV, однако не соответствует установленному сроку окупаемости в 3 года, поскольку его DPP=4, и формально должен быть отклонен. Таким образом, в соответствии с инвестиционной политикой фирмы для реализации должен быть выбран проект «А». Очевидно, что при этом не достигается основная цель — максимизация стоимости фирмы и благосостояния ее собственников.
Таблица П1.3.6. Объемы инвестиций и дисконтированные денежные потоки проектов, тыс. руб.
| Период | Проект | |||
| «А» | «Б» | «В» | «Д» | |
| -1000 | -2000 | -1000 | -1000 | |
| -1000 | ||||
| -10 000 | ||||
| NPV | - 9700 |
Критерий DPP обладает и другими недостатками, вследствие чего его не рекомендуется использовать самостоятельно. Как правило, он дополняет анализ критериев NPV и IRR.
Подводя итоги, отметим, что среди рассмотренных подходов показатель NPV позволяет получить наиболее достоверные результаты. Вместе с тем корректным подходом к анализу эффективности долгосрочных инвестиций является применение всех рассмотренных показателей, так как в совокупности они обеспечивают лиц, принимающих инвестиционные решения, более полной информацией.
На практике часто возникает необходимость сравнения проектов с различными сроками. Формальным инструментом оценки в подобных ситуациях является метод эквивалентного аннуитета (Equivalent Annual Annuity — ЕАА), который включает в себя три этапа.
· определяют NPV каждого из сравниваемых проектов;
· вычисляют эквивалентный аннуитет ЕАА, стоимость которого равна NPV потока проекта, по формуле
|

· полагая, что каждый проект может быть повторен бесконечное число раз, т. е. переходя к бессрочному аннуитету, находят его стоимость по формуле
|
 .
.
Пример П1.3.8. Имеются два альтернативных проекта «А» и «В», потоки платежей и расчет критериев эффективности для которых представлены в табл. П1.3.7. Ставка дисконтирования принята 11,5%.
 Как следует из приведенной таблицы, проект «А» при дисконтировании по ставке 11,5%, равной цене капитала, имеет более высокое значение NPV и,следовательно, является предпочтительным. Хотя IRR проекта «В» выше, основываясь на критерии NPV, можно все же считать проект «А» лучшим. Вместе с тем данный вывод не представляется бесспорным, поскольку при выборе проекта «В» появляется гипотетическая возможность реализовать его через 3 года еще раз.
Как следует из приведенной таблицы, проект «А» при дисконтировании по ставке 11,5%, равной цене капитала, имеет более высокое значение NPV и,следовательно, является предпочтительным. Хотя IRR проекта «В» выше, основываясь на критерии NPV, можно все же считать проект «А» лучшим. Вместе с тем данный вывод не представляется бесспорным, поскольку при выборе проекта «В» появляется гипотетическая возможность реализовать его через 3 года еще раз.
Таблица П1.3.7. Ожидаемые денежные потоки и критерии эффективности по проектам, тыс.руб.
| Год | Проект | |
| «А» | «В» | |
| -40 000 | -20 000 | |
| 14 000 | 13 000 | |
| 13 000 | 12 000 | |
| 12 000 | — | |
| 11 000, | — | |
| 10 000 | — | |
| NPV | ||
| IRR,% | 17,5 | 25,2 |
Проведем анализ данной ситуации с помощью метода эквивалентного аннуитета. Поскольку ЛТК проектов заданы, переходим сразу к шагу 2. Определим величины ЕААА и ЕААВ:


Определим NPV аннуитетов при n→∞:
NPVA = 1718 / 0,115 = 14939 тыс. руб.; NPVB = 2225 / 0,115 = 19348тыс. руб. IRR.
Сравнивая полученные данные, можно сделать вывод о том, что проект «В» более предпочтителен.
Еще одним методомоценки экономической эффективности инвестиционных проектов является метод скорректированной текущей стоимости (adjusted present value - APV). Оценка экономической эффективности проекта с использованием метода АРV осуществляется в четыре этапа:
1)подготовка прогноза денежного потока (бюджета капиталовложений);
2) дисконтирование ожидаемого денежного потока от операций (определение NPV) после вычета налогов по ставке rЕ, равной стоимости (норме доходности) собственного капитала при условии отсутствия у фирмы долга;
3) оценка приведенной стоимости последствий различных финансовых решений;
|

Правило принятия решений такое же, как и у метода NPV:
 |
При этом к числу наиболее значимых и распространенных на практике финансовых эффектов обычно относят:
• (+) налоговый щит (процентная налоговая защита, возникающая при использовании заемного финансирования);
• (+) правительственные и прочие субсидии, гранты, льготы и т. п.;
• (-) эмиссионные издержки;
• (-) стоимость страхования рисков;
• (-) возможные издержки финансовых затруднений и банкротства и др.
Как уже отмечалось, на практике часто ограничиваются оценкой влияния эффекта налогового щита. При этом формула (1.3.10)принимает следующий вид:
|

где I – проценты по займу; Т – ставка налога на прибыль; rD – доналоговая стоимость займа.
Пример П1.3.9. Рассматриваемый проект, требующий первоначальных инвестиций в объеме 4 млн. руб. Предполагается, что финансирование проекта будет осуществляться за счет займа в 2,5 млн. руб., привлеченного под 13% годовых, а оставшиеся 1,5 млн. ед. составят вложения собственников фирмы, требуемая норма доходности которых равна 20%. Предварительный анализ показал, что посленалоговый операционный поток платежей от проекта составит 1,2 млн. руб. на протяжении 6 лет. Планируется, что по истечении данного срока проект будет реализован по остаточной стоимости, которая составит 2 млн. ед. после вычета соответствующих налогов. Привлеченный заем будет погашаться равными выплатами в течение 6 лет. Ставка налога на прибыль — 24%. Определим экономическую эффективность данного проекта методом APV.
В соответствии с изложенным алгоритмом определим базовую JVPK проекта, дисконтируя операционные потоки по требуемой собственниками ставке доходности rЕ = 20%:

Реализация следующего этапа - определение стоимости финансовых эффектов, которыми в данном примере выступают выгоды от заемного финансирования (налоговый щит), требует выполнения ряда подготовительных действий. Поскольку налоговый щит создают только процентные платежи, а периодические выплаты по погашению кредита включают в себя как проценты, так и основную часть долга, возникает необходимость их выделения из общей суммы в каждом временном периоде. Решение этой задачи осуществляется путем разработки плана погашения займа.
Согласно условиям предоставления займа задолженность погашается равными суммами в течение срока реализации проекта, т. е. CF1 = CF2 =... = CF6, = CF= const, и возникающий при этом поток платежей представляет собой обыкновенный аннуитет. Планирование выплат по займу в данном случае осуществляется в два этапа. На первом этапе необходимо определить величину периодического платежа CF. Данная величина может быть найдена по формуле:
|
 ,
,
где D - сумма займа; r - процентная ставка; CF- периодический платеж.
В рассматриваемом примере величина ежегодного платежа CF по погашению кредита составит:
CF= 2,5 × [0,13 ×(1 + 0,13)6 / (1 - (1 + 0,13))] = 0,6254 млн.ед.
|
|
St = St-1 × (1+r).
|
It=CF-St.
Полный расчет плана погашения долга для примера П1.3.9 приведен в табл.П1.3.8.
Таблица П1.3.8. План погашения кредита, млн. руб.
| Показатель | Период | Итого | |||||
| 2 | |||||||
| Основная сумма долга (S,) | 0,3004 | 0,3394 | 0,3836 | 0,4334 | 0,4898 | 0,5534 | -2,5000 |
| Процентная часть (It) | 0,3250 | 0,2860 | 0,2418 | 0,1920 | 0,1356 | 0,0719 | -1,2523 |
| Периодический платеж (CF) | 0,6254 | 0,6254 | 0,6254 | 0,6254 | 0,6254 | 0,6254 | -3,7523 |
Теперь можно рассчитать приведенную стоимость эффекта от использования заемного финансирования дисконтированием потока процентных выплат по ставке стоимости долга rD - 13%:
 Соответственно, величина АРV длярассматриваемого проекта APV= NPV+ PV1 = 0,66 + 0,2172 = 0,8776 млн. руб.
Соответственно, величина АРV длярассматриваемого проекта APV= NPV+ PV1 = 0,66 + 0,2172 = 0,8776 млн. руб.
Одним из наиболее важных преимуществ метода проявляется его гибкость: он позволяет разделить денежные потоки инвестиционного проекта и провести их оценку раздельным дисконтированием с использованием соответствующих ставок. Есть также возможность проанализировать различные источники создания стоимости проекта.
Так, в рассмотренном примере свыше 75% ценности проекта (величины APV) создается за счет его основной деятельности (выпуска и реализации продукции), а вклад выгод от использования заемного финансирования составляет 24,75%.
В последние десятилетия был предложен ряд усовершенствованных показателей прибыли и рентабельности, наибольшее распространение из которых получил такой критерий, как экономическая добавленная стоимость (economic value added — EVA) и его аналоги.
Базовая формула расчета экономической стоимости за период t:
|
где NOPAТ - чистая операционная прибыль проекта за вычетом налогов; Т - ставка налога на прибыль; WACC - средневзвешенная стоимость капитала; 1С - инвестированный капитал.
|
NOPAТ = ЕВ1Т(1 - Т)
|
EVAt = ЕВ1Тt (1 -Т) - WAСС ×IСt-1
Таким образом, EVA представляет собой денежную оценку стоимости, создаваемой для инвесторов за определенный период времени проектом сверх ожидаемой нормы доходности капиталовложений с аналогичным уровнем риска.
Теоретически метод оценки эффективности инвестиций на основе EVA дает тот же результат, что и NPV-анализ. Далее приводится формальное доказательство данного утверждения.
|

Инвестированный капитал:
|

Подставив (1. 3.21) в (1.3.20), после незначительных преобразований получим:
|

Предположим, что приведенная стоимость амортизационных отчислений за время функционирования инвестиционного проекта, выраженная последним слагаемым в (1.3.19), равна начальным инвестициям, т. е.:
|
 .
.
Тогда с учетом имеем:
|

Таким образом, величина MPF инвестиционного проекта равна приведенной стоимости ежегодных EVA в течение срока его реализации. Поэтому критерий EVA может быть использован как альтернативный способ оценки инвестиционных проектов.
Пример П1.3.10. Оценивается проект, требующий первоначальных вложений в объеме 1000 тыс. руб. Предполагается, что срок функционирования проекта составит 5 лет. Требуемая инвесторами ставка доходности r (стоимость используемого капитала WACС) равна 10%, а налога на прибыль — 24%. Прогноз основных параметров проекта представлен в табл. П1.3.9. Фирма использует линейный способ амортизации основных активов.
Таблица П1.3.9. Прогноз прибыли и затрат по проекту, тыс. руб.
| Показатель | Период | ||||
| Доналоговая операционная прибыль (EBIT) | |||||
| Величина инвестированного капитала (IС)1 | |||||
| Амортизация основных активов (DA) |
Определим экономическую эффективность реализации данного проекта по методу EVA и NPV. Для оценки показателя EVA в каждом периоде воспользуемся прогнозными данными. Полный расчет показателей EVA, для рассматриваемого примера представлен в табл. П1.3.10.
Таблица П1.3.10. Расчет эффективности проекта по методу EVA, тыс. руб.
| Показатель | Период | ||||
| Доналоговая операционная прибыль (EBIT) | |||||
| Налог на прибыль (Т = 0,24) | |||||
| Посленалоговая операционная прибыль (NOPAT) | |||||
| Затраты на капитал (1Сt × WACC) | |||||
| Экономическая стоимость (EVA) |
Полученные величины EVA отражают эффективность реализации проекта на каждом шаге планирования. С целью оценки интегрального экономического эффекта,
а также учета в анализе факторов времени, риска и альтернативности стоимости капитала необходимо дисконтировать полученные показатели EVA по заданной ставке r (r = WACC). Определим приведенную стоимость величин EVA1:

Теперь рассчитаем экономическую эффективность рассматриваемого проекта по методу NPV. Для этого необходимо определить денежные потоки СF, по проекту для каждого периода t. Как следует из (1.3.14), величина денежного потока для шага t может быть получена добавлением к операционной прибыли после вычета налога (NOPAT) суммы амортизации за соответствующий период (DA).
Тогда NPV проекта будет равна:

Использование EVA в качестве инструмента оценки эффективности инвестированного капитала по периодам времени позволяет менеджерам компании принимать более обоснованные решения по расширению прибыльных направлений деятельности и, что не менее важно, помогает выявить неэффективное использование средств в проектах, рентабельность которых не покрывает затраты на привлечение капитала.
1.4. Методы выбора оптимального варианта проектных решений
Для обоснования эффективности предлагаемого нового устройства необходимо провести сравнение проектируемого устройства с существующими аналогами или другими вариантами его реализации. В данном пособии подробно рассмотрены три метода, наиболее часто используемые для выбора оптимального варианта: таксонометрический метод, метод анализа иерархий и квалиметрический метод [5, 10, 12].
Для этой цели из всех параметров, характеризующих устройство с точки зрения его технических качеств и экономических показателей, выбираются наиболее существенные, из которых формируется набор критериев для осуществления выбора оптимального варианта. Очевидно, что такая задача носит многокритериальный характер. Поскольку параметры, участвующие в сопоставлении, чаще всего несопоставимы по сущности и единицам измерения, то используется прием «нормализации», позволяющий сопоставлять параметры, различные по сути. Кроме того, в зависимости от назначения проектируемого устройства степень влияния каждого из параметров на качество и эффективность устройства в большинстве случаев бывает различной, поэтому необходимо
учитывать «вес» (значимость) показателей при проведении сравнений с помощью весовых коэффициентов.
Сущность таксонометрического метода сравнения вариантов состоит в проведении сопоставления совокупности показателей на основе дисперсионного анализа с учетом их значимости. Для осуществления сравнения нужно построить матрицу, содержащую n*m значений показателей Аij,, подлежащих сравнению, где i = 1, n - количество показателей, по которым осуществляется сравнение; j=l,m - количество сравниваемых объектов.
Рассмотрим пример 1.4.1 по выбору наилучшего устройства, для которого ключевыми показателями, определяющими его эффективность, являются: чувствительность, надежность, технологичность, вес и себестоимость. Каждый из этих показателей в зависимости от назначения устройства в разной степени влияет на степень его эффективности. Так, для одних целей применения чувствительность и надежность являются более важными параметрами, чем низкая себестоимость. Напротив, в других обстоятельствах определяющим фактором является себестоимость. Поэтому в зависимости от важности показателя относительно других задается «вес» каждого параметра Lj (табл. 1.4.1).
Таблица 1.4.1. Пример оценки веса параметров устройства
| Наименование параметра, ед. измерения | Обозначение параметра | Вес Lj | Коэффициент весомости gi |
| Себестоимость, руб. | Ст | 0,11 | |
| Чувствительность, мкВ | Ч | 0,39 | |
| Технологичность | Т | 0,28 | |
| Срок службы, час. | СС | 0,17 | |
| Вес, кг. | В | 0,06 | |
| Итого | 1,00 |
«Вес» каждого показателя может быть оценен экспертной комиссией. При осуществлении ВКР эту функцию может на себя брать руководитель дипломного проекта. Для осуществления сравнения выбирается балльная шкала степени важности показателей, где с ростом баллов увеличивается «вес» параметра, то есть его важность.
Далее для каждого параметра рассчитывается коэффициент весомости gi, представляющий собой отношении каждого конкретного значения веса к общей сумме весов всех показателей:
 (1. 4. 1)
(1. 4. 1)
Например, коэффициент весомости параметра себестоимости равен gi =2/18=0,11. При этом сумма всех коэффициентов gi всегда равна 1.
Для пояснения методики выбора оптимального варианта построим матрицу сравнения трех моделей устройств М1, М2, М3 с конкретными значениями параметров Аij. и их «весов» (табл. 1.4.2)..В данной матрице i=l,5; j=l,3. Для каждого параметра введем признак Si, который примем равным Si=+1, если при возрастании величины параметра улучшается качество устройства, и Si= -1, если, напротив, качество устройства падает при возрастании значения параметра. Например, если себестоимость устройства растет, то при прочих равных такое устройство будет хуже, чем его более дешевый аналог, и в этом случае Si= -1. В то же время, если растет чувствительность, то это повышает качество устройства, то Si = +1.
Для сравнения разнородных величин все элементы составленной матрицы Аij необходимо нормировать и сформировать новые значения элементов матрицы Zij. Рассматриваемый метод использует следующую форму нормирования:
 , (1. 4. 2)
, (1. 4. 2)
где 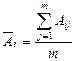 - среднее значение;
- среднее значение;  - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Для наглядности расчетов в табл. 1.4.2 введены столбцы промежуточных значений (среднее, среднее квадратическое отклонение) и значения нормированной матрицы для трех моделей Zi1, Zi2, Zi3, вычисленных по формуле (1.4.2). Выбранные значения эталона сравнения Zj0 также заносятся в табл.1.4.2. Эталон сравнения – это модель с наилучшими из возможных значений параметров, для чего должны соблюдаться условия: Zi0 = max {Zij} при Si = +1;
Zi0 = min {Zij } при Si = -1.
Выбор устройства, которое наиболее близко к эталону по большинству показателей, осуществляется с помощью показателя Rj:
 . (1. 4. 3)
. (1. 4. 3)
В нашем примере это R1 R2, R3. Устройство, у которого показатель Rj имеет минимальный уровень (min{ Ri }), в наименьшей степени отличается от эталона и является лучшим из всех рассматриваемых. Следовательно, наилучшим является устройство M1.
Рассмотренный способ сравнения рекомендуется применять при наличии не менее трех сравниваемых вариантов, что обусловлено требованиями статистики для нормирования данных. Если существует лишь один вариант для сравнения, то целесообразно применить метод анализа иерархий, который позволяет сравнивать любое количество вариантов.
Таблица 1.4.2. Выбор наилучшего варианта технического устройства таксонометрическим методом
| Критерий | Ед. измер. | М1 | М2 | М3 | S | Вес Мi | Коэфф. весомости Gi | Средняя величина | Ср.кв. откл |  i1 i1
| Zi2 | Zi3 | Эталон Zi0 | R1 | R2 | R3 | MIN R |
| СТ | руб. | -1 | 0,13 | 901,85 | -0,07 | 1,03 | -0,96 | -0,96 | 1,00 | 2,11 | 1,90 | 1,00 | |||||
| Ч | мКв | 0,44 | 7,667 | 2,0817 | 1,12 | -0,80 | -0,32 | 1,12 | |||||||||
| Т | год | 1,17 | 1,25 | 1,05 | 0,19 | 1,157 | 0,1007 | 0,13 | 0,93 | -1,06 | 0,93 | ||||||
| В | кг | -1 | 0,06 | 46,67 | 7,7675 | 0,30 | -1,12 | 0,82 | -1,12 | ||||||||
| СС | час. | 0,19 | 2779,1 | -1,14 | 0,73 | 0,41 | 0,73 |
Как и в предыдущем методе, сначала определяется перечень параметров - критериев (i = 1,n), по которым проводится оценка качества устройства, и производится выбор сравниваемых вариантов Mj (j=1,m) - альтернатив. Иерархия строится с вершины - цели анализа (в нашем случае, это - наилучшая модель устройства, которую надо выбрать), через промежуточные уровни (критерии, по которым производится сравнение вариантов), к нижнему уровню, который является перечислением альтернатив Mj. Пример иерархии для выбора одного варианта устройства из трех по N критериям представлен на рис. 1.4.1.
 |
Рис.1.4.1. Иерархия для выбора наилучшей модели устройства
Суть метода заключается в том, что первоначально определяется важность («вес») каждого критерия (в работе [10] предложена шкала относительной важности критериев, представленная в табл. 1.4.3). После этого производятся парные сравнения критериев для оценки их относительных весов. Затем проводится парное сравнение альтернатив относительно каждого из рассматриваемых критериев и производятся интегральные оценки каждого из вариантов, полученные с учетом оценок по всем критериям. Лучший вариант выбирается путем сравнения интегральных оценок.
Для пояснения принципа использования метода МАИ применим его на конкретном примере 1.4.2 устройства Ml. Будем считать, что у этого устройства существует аналог М2 с известными параметрами и нам необходимо выбрать лучший из двух аналогов, причем мнения экспертов по поводу преимуществ каждого из них совпадают. Воспользуемся перечнем параметров, важных для оценки качества устройств, приведенным в примере 1.4.1. Их «веса», оцененные по пятибалльной системе, и значения критериев приведены в табл. 1.4.4.
Таблица 1.4.3. Шкала относительной важности критериев
| Важность | Определение | Комментарий |
| Равная важность | Равный вклад двух видов деятельности в реализацию цели | |
| Умеренное превосходство одного над другим | Опыт и суждения дают лёгкое превосходство одному виду деятельности над другим | |
| Существенное или сильное превосходство | Опыт и суждения дают сильное превосходство одному виду деятельности над другим | |
| Значительное превосходство | Одному виду деятельности даётся настолько сильное превосходство, что оно становится практически значительным | |
| Очень сильное превосходство | Высокая очевидность превосходства одного вида деятельности над другим | |
| 2, 4, 6, 8 | Промежуточные решения между двумя соседними суждениями | Применяются в компромиссном случае |
| Обратные величины приведен-ных выше чисел | Если при сравнении одного вида деятельности с другим получено одно из вышеуказанных чисел, то при сравнении второго вида деятельности с первым получим обратную величину |
Таблица 1.4.4. Исходные данные, взятые из таблицы 1.4.1
| Наименование критерия, единица измерения | Обозначение критерия | Вес Li | М1 | М2 |
| Себестоимость, руб. | Ст | |||
| Чувствительность, мкВ | Ч | |||
| Коэффициент технологичности | Т | 1,17 | 1,25 | |
| Срок службы, час. | СС | |||
| Вес, кг. | В | |||
| Итого |
Построим матрицу парных сравнений второго уровня иерархии - сравнение критериев между собой по степени их важности. В нулевой столбец и нулевую строку занесены обозначения критериев. Элементы матрицы обозначим Aij, причем i = l,n; j = 1,n, то есть матрица квадратная, (табл. 1.4.5, где приведены относительные веса критериев). Кроме того, в соответствии с методикой МАИ матрица является обратно симметричной, то есть элементы матрицы соотносятся между собой как:
 (1.4.4)
(1.4.4)
Таблица 1.4.5. Матрица парных сравнений
| В | Ч | Т | СС | СТ | |
| В | 1/5 | 1/3 | 1/2 | 1/2 | |
| Ч | |||||
| Т | 1/2 | ||||
| СС | 1/3 | 1/2 | |||
| Ст | 1/2 | 1/2 |
В первый столбец квадратной матрицы занесем «веса» критериев, а в первую строку их обратные значения в соответствии с выражением (1.4.4) - так критерий В (вес устройства) соотносится с другими критериями по степени важности в соответствии с принятыми экспертом весами. Далее во второй строке производится сравнение критерия Ч (чувствительность) попарно с другими критериями, и выставляются баллы также, исходя из собственного суждения о сравнительной важности критериев, в соответствующих ячейках второй строки таблицы. Таким же способом заполняются следующие строки матрицы.
Далее определяются векторы приоритетов Wi (табл. 1.4.6), для которых справедливы следующие выражения:
 , (1.4.5)
, (1.4.5)
 , где n – размерность матрицы.
, где n – размерность матрицы.
ж
Таблица 1.4.6. Определение векторов приоритетов для критериев
| В | Ч | Т | СС | СТ | Произведение | pi | Wi | |
| В | 1/5 | 1/3 | 1/2 | 1/2 | 0,0167 | 0,44 | 0,03 | |
| Ч | 60,00 | 2,27 | 0,90 | |||||
| Т | 1/2 | 6,00 | 1,43 | 0,33 | ||||
| СС | 1/3 | 1/2 | 0,33 | 0,8 | 0,11 | |||
| Ст | 1/2 | 1/2 | 0,5 | 0,87 | 0,13 | |||
| Si | 2,53 | 4,33 | 7,50 | 6,50 |
Например, 

Поскольку заполнение ячеек матрицы производится экспертами на основании их субъективных оценок, что не исключает наличие несогласованности матрицы, а следовательно, и формирования ошибочного заключения при выборе устройства, необходимо произвести проверку согласованности матрицы парных сравнений. Для этого вычисляется выражение:
 . (1.4.6)
. (1.4.6)
После чего рассчитываются индекс согласованности ИС и отношение согласованности ОС
Поиск по сайту: