 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Примеры решения по теме 5: Интегральные исчисления
а) Вычислить 
Данный интеграл вычисляется методом замены переменной.
Решение:

Проведем дифференцирование:
 – подынтегральная функция
– подынтегральная функция
б) Вычислить 
Решение: интеграл вычисляется по частям: 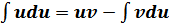
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Аналогично можно проверить. Что произведение полученной функции равно подынтегральной функции, т.е интеграл вычислен правильно.
в) Вычислить 
Решение.
При вычислении переделенного интеграла используются такие же методы что и неопределенного. Но затем пользуются формулой Ньютона- Лейбница:


г) Найти площадь фигуры: у=х2-2х – парабола с вершиной в точке (1;-1), ветви вверх точка пересечения с осью ОХ: (0;0); (2;0)

s=s1+s2;



Тема: Комплексные числа. Алгебраическая форма комплексного числа a+bi; {a,b}ªR, i- мнимая единица, i2=-1
Сложение:
z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i
(2+3i)+(5-7i)=(2+5)+(3-7)i=7-4i
Вычитание:
z1-z2 =(a+bi)-(c+di)=(a-c)+(b-d)i
(5+4i)-(2-3i)=(5-2)+(4+3)i=3+7i
Умножение:
z1*z2=(a+bi)*(c+di)=(ac-bd)+(ad+bc)
(a+bi) на (c+di) умножаем по правилам действий над многочленами.
(1+2i)(3-i)=3*1-1*i+6i-2i2=3+2-i+6i=5+5i
Деление: на практике при делении комплексных чисел удобно домножить числитель и знаменатель дроби на выражении, сопряженное знаменателю:


Возведение в степень мнимой единицы:
i1=i;
i2=-1;
i3=i2*i=-1*i=-i;
i4=i2 *i2=(-1)(-1)=1;
i5=i3*i2=-i(-1)=i;
i6=i5*i=i*i=-1=i2;…
Видим закономерность:
i(4n+r)=(i4)n*ir=(1)n*ir=ir
Получаем:
i4m=1;
i4m+1=i;
i4m+2=-1;
i4m+3=-i;
i218=i4*54+2=i2=-1.
Сумма и произведение двух сопряженных комплексных чисел являются действительными числами:
z+z=(a+bi)+(a-bi)=2a;
z*z=(a+bi)(a-bi)=a2+b2.
Каждому комплексному числу z=a+bi можно поставить в соответствие точку M(a;b) координатной плоской, абсцисса которой равна действительной части комплексной части комплексного числа, а ордината - мнимой части (рис.)
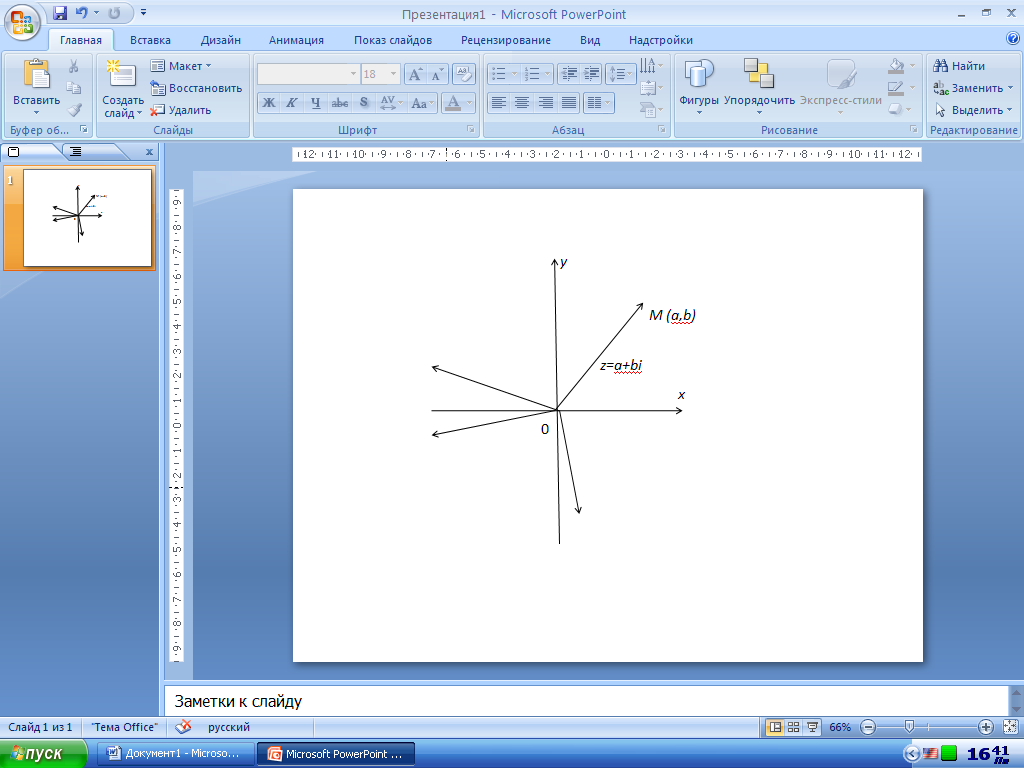
Рис.
Важной и удобной является интерпретация комплексного числа a+bi как радиус - вектора OM, т.е. вектора, исходящего из начала координат O(0,0) и идущего в точку M(a;b). Разумеется, вместо радиус вектора OM можно взять любой равный ему вектор. Изображение комплексных чисел с помощью векторов удобно тем, что при этом получают простое геометрическое истолкование операций над ними. При сложении чисел z1=a+bi и z2=c+di складываются их действительные и мнимые части. При сложении соответствующих им векторов OM1 и OM2 складываются их координаты:
числу z1+z2 соответствует вектор OM1+OM2,
числу z1-z2 – вектор OM1 – OM2.
Модулем комплексного числа z1=a+bi называется арифметический квадратный корень из суммы квадратов его действительной части и коэффициента при мнимой единице:

Аргументом комплексного числа z1=a+bi называется радианная мера угла φ, образованного этим вектором с положительным направлением действительной оси 0≤φ<2π,
arg z=φ
Величина угла считается положительной, если отсчет ведется против часовой стрелки и отрицательной, если отсчет производится по часовой стрелке.
Возьмем на плоскости точку М(a,b), пусть ей соответствует комплексное число z1=a+bi. Обозначим через φ угол, который образует радиус – вектор OM с положительным направлением оси OX.
Тригонометрическая форма комплексного числа r(cosφ+ isinφ), показательная форма reφi
Действия в показательной форме:


 - формула Муавра.
- формула Муавра.
Аналогично в тригонометрической форме:
Пример.



Тема 3. Действия с приближенными числами.
a=35,671±0,0023
∆a=0,0023 –абсолютная погрешность а; ha=0,01- граница погрешности
b=17,5231±0,01
∆b=0,01 - 1 – b, она же граница абсолютной погрешности hb
Округляют с верными цифрами a и b:По правилам подсчёта верных цифр:
a≈35,67;b≈17,53
a∙b=35,67∙17,53=
a+b=53,20;
a-b=18,14;
a:b=35,67:17,53=
Правила:
1) При сложении вычитании результат округляют с наименьшим числом десятичных знаков среди исходных данных
2) При умножении и делении, а так же комбинированных действиях. Результат округляют с наименьшим числом значащих цифр, оставляя запасную цифру в промежуточных действиях, исходные данные округляют так же с запасной цифрой, предварительно округлив до верных цифр.
Литература:
1. Кремер Н.Ш. Практикум по высшей математике.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. I. М: Высшая школа, 1999
3. Письменный Д.Т.Сборник задач по высшей математике,М:Айрис-пресс, 2004
4. Письменный Д.Т. Конспекты лекций по высшей математике ч. I, М: Айрис-пресс, 2006
5. Валуцэ Н.И., Дилигул Г.Д. Математика для техникумов. Наука, 1980
6. Габзалилова Л.В. Учебное пособие. Дискретная математика, УТЭК, 2009
7. Пехлецкий И.Д. Математика. М: ACADEMA, 2009
Поиск по сайту: