 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема 1. Элементы теории множеств
01-10. Для данных множеств M и N найти: M U N; M ∩ N; N/М;M/N;
M x N; M + N.
Совокупность всех подмножеств множества M:
01. M={5;6;8}; N={2;3;4;5};
02. M={p;3;e}; N={1;2;p;e};
03. M={12;13;15}; N={11;12;13;15}
04. M={a;b;c}; N={b;c;d;e}
05. M={2;3;5} N={5;6;8;9}
06. M={2;3;4} N={1;4;5;6}
07. M={1;2;3} N={3;4;5;6}
08. M={3;4;5} N={4;5;6;7}
09. M={2;3;e} N={3;e;2;2;}
10. M={6;7;9} N={3;4;5;6}
№ 11-20 Тема 2. Решение линейных систем уравнений методами
а) Крамера, б)Гаусса
11.
а)  б)
б) 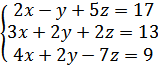
12.
а)  б)
б) 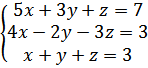
13.
а) 
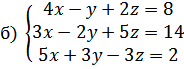
14.
 б)
б) 
15.
а)  б)
б) 
16.
a) 

17.
 б)
б) 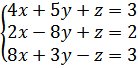
18.
 б)
б) 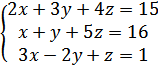
19.
 б)
б) 
20.


Тема 3. Элементы комбинаторики. [6], гл 5, п1-3
21-30. 21. Решить уравнение: 
22. Решить уравнение: 
23. Сколько способов распределения 3 одинаковых путевок в дом отдыха среди 5 рабочих цехов?
24. Сколько способов распределения путевок в санаторий, дом отдыха и в турбазу среди 5 рабочих цехов?
25. Решить уравнение: 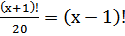
26. Сколько способов расставить 10 различных книг на полке?
27. Сколько трехзначных чисел можно образовать из цифр 2;8;7 без повторных цифр?
28. Сколько двухзначных чисел можно образовать из цифр 2;8;7 без повторных цифр?
29. Сколько четырехзначных чисел можно образовать из цифр 1;2;3;4 без повторных цифр?
30. Сколькими способами можно распределить 12 человек по бригадам по 6 человек в каждом?
Тема 4. Дифференциальное исчисление [1], гл. 7,8 §1,2 [3], §20,24
№ 31-40 Найти:
а) Производную и дифференциал функции
б) Наибольшее и наименьшее значение на [а;b]
31. a) 
б) 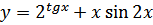
в) 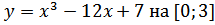
32. a) 
б) 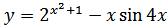
в) 
33. a) 
б) 
в) 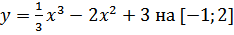
34. a) 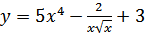
б) 
в) 
35. a) 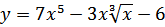
б) 
в) 
36. a) 
б) 
в) 
37. a) 
б) 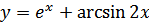
в) 
38. a) 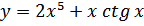
б) 
в) 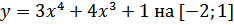
39. a) 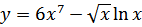
б) 
в) 
40. a) 
б) 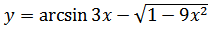
в) 
Тема 5. Интегральное исчисление [3]гл. 9,10 § 1,2 [1] гл. 10,11 § 1,2
№ 41-50. Найти интегралы в п. а), б), в) и площадь фигуры, ограниченный линиями в п. г)
41. a) 
б 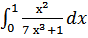 )
)
в) > 
г) 
42. a) 
б) 
в) 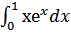
г) 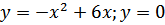
43. a) 
б) 
 в)
в) 
г)y= 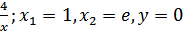
44. а) 
б) 
в) 
г) 
45. а) 
б) 
в) 
г)y= 
46. а) 
б) 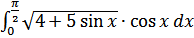
в) 
г) 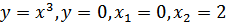
47. а) 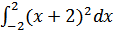
б) 
в) 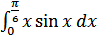
г) 
48. а) 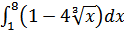
б) 
в) 
г) 
49. а) 
б) 
в) 
г) 
50. а) 
б) 
в) 
г) 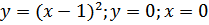
Тема 6. Дифференциальные уравнения [1], гл.12 § 1, 2
51-60
Найти решение дифференциальных уравнений
а) общее,
б) частное
51.
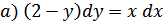 ; б)
; б) 
52.
 ; б)
; б) 
53.
а) 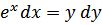 ;
; 
54.
 ;
; 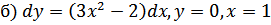
55.
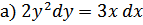 ;
; 
56.
а) 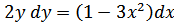 ;
; 
57.
 ;
; 
58.
 ;
; 
59.
 ;
; 
60.
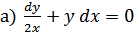 ;
; 
Тема 7. Элементы теории графов. [6], гл 4, п1-4
№61-70. Для графа найти:
а) множество вершин, дуг и ребер, вид графа.
б) матрицу смежности вершин.
в) матрицу ребер и вершин.
г) маршруты длины 2.
| b |
| a |
61. 62.
| c |
| d |
65. 1 2 66. 1 2
3 4 4 3
67. 1 2 68. 1 2
4 3 3 4
69. 1 2 70. A b
4 3 d с
Поиск по сайту: