Множества и его элементы. Подмножества

Определение:

Множество – это любая совокупность объектов, которые называются его элементами.

Если х- элемент множества М, то обозначают: х М { х – принадлежит М}, если не принадлежит, то х ∉ М; Множество не содержащее элементов называется пустым и обозначается ∅

Множество, в котором содержатся все элементы, находящиеся в рассмотрении, называется универсальным или универсумом и обозначается –

Ư. Множества, состоящие из одних и тех же элементов, называются равными и обозначаются А = В.

Если любой элемент множества В является элементом множества А, то множество В называется подмножеством множества А (частью множества А) и обозначается В ⊂ А; Отсюда следует, что любое множество является частью самого себя.

По определению пустое множество ∅ является подмножеством любого множества. Т.о. у любого множества А есть два подмножества:

А и ∅.

Они называются несобственными подмножествами множества А. Любое множество В множества А, которое не является несобственными подмножествами А, (т.е. они отличны от А и ∅) и называются собственными подмножествами подмножества А. Множество из одного элемента а обозначается {а}.

Пример: А = {1;2;3} тогда пустое множество ∅ и само множество А является несобственными подмножествами А.

Множества:{1},{2},{3},{1;2},{1;3},{2;3} называются собственными подмножествами множества А. Совокупность всех множеств А называется его булеаном и обозначается – 2^А; В А, означает, что В 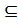А, В ≠ А. В этом случае говорят, что В строго включено в А или В является собственным подмножеством А;

В случае В ⊆ А, В = А говорят, что В нестрогое включение в А, т.е. В является несобственным подмножеством А.

Поиск по сайту: